Correlation Matix Visualization with Package Seriation

Author

Michael Hahsler

Introduction

A correlation matrix is a square, symmetric matrix showing the pairwise correlation coefficients between two sets of variables. Reordering the variables and plotting the matrix can help to find hidden patterns among the variables. The package seriation implements a large number of reordering methods (see: the list with all implemented seriation methods). seriation also provides a set of functions to display reordered matrices:

  • pimage()
  • ggpimage()

How to cite the seriation package:

Hahsler M, Hornik K, Buchta C (2008). “Getting things in order: An introduction to the R package seriation.” Journal of Statistical Software, 25(3), 1-34. ISSN 1548-7660, doi:10.18637/jss.v025.i03 https://doi.org/10.18637/jss.v025.i03.

Prepare the data

As an example, we use the mtcars dataset which contains data about fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973-74 models).

if (!require("seriation")) install.packages("seriation")
Loading required package: seriation
library("seriation")
data("mtcars")

DT::datatable(mtcars)

We calcualte a correlation matrix.

m <- cor(mtcars)
round(m, 2)
       mpg   cyl  disp    hp  drat    wt  qsec    vs    am  gear  carb
mpg   1.00 -0.85 -0.85 -0.78  0.68 -0.87  0.42  0.66  0.60  0.48 -0.55
cyl  -0.85  1.00  0.90  0.83 -0.70  0.78 -0.59 -0.81 -0.52 -0.49  0.53
disp -0.85  0.90  1.00  0.79 -0.71  0.89 -0.43 -0.71 -0.59 -0.56  0.39
hp   -0.78  0.83  0.79  1.00 -0.45  0.66 -0.71 -0.72 -0.24 -0.13  0.75
drat  0.68 -0.70 -0.71 -0.45  1.00 -0.71  0.09  0.44  0.71  0.70 -0.09
wt   -0.87  0.78  0.89  0.66 -0.71  1.00 -0.17 -0.55 -0.69 -0.58  0.43
qsec  0.42 -0.59 -0.43 -0.71  0.09 -0.17  1.00  0.74 -0.23 -0.21 -0.66
vs    0.66 -0.81 -0.71 -0.72  0.44 -0.55  0.74  1.00  0.17  0.21 -0.57
am    0.60 -0.52 -0.59 -0.24  0.71 -0.69 -0.23  0.17  1.00  0.79  0.06
gear  0.48 -0.49 -0.56 -0.13  0.70 -0.58 -0.21  0.21  0.79  1.00  0.27
carb -0.55  0.53  0.39  0.75 -0.09  0.43 -0.66 -0.57  0.06  0.27  1.00

We first visualize the matrix without reordering and then use the order method "AOE". AOE stands for angle of eigenvectors and was proposed for correlation matrices by Friendly (2002).

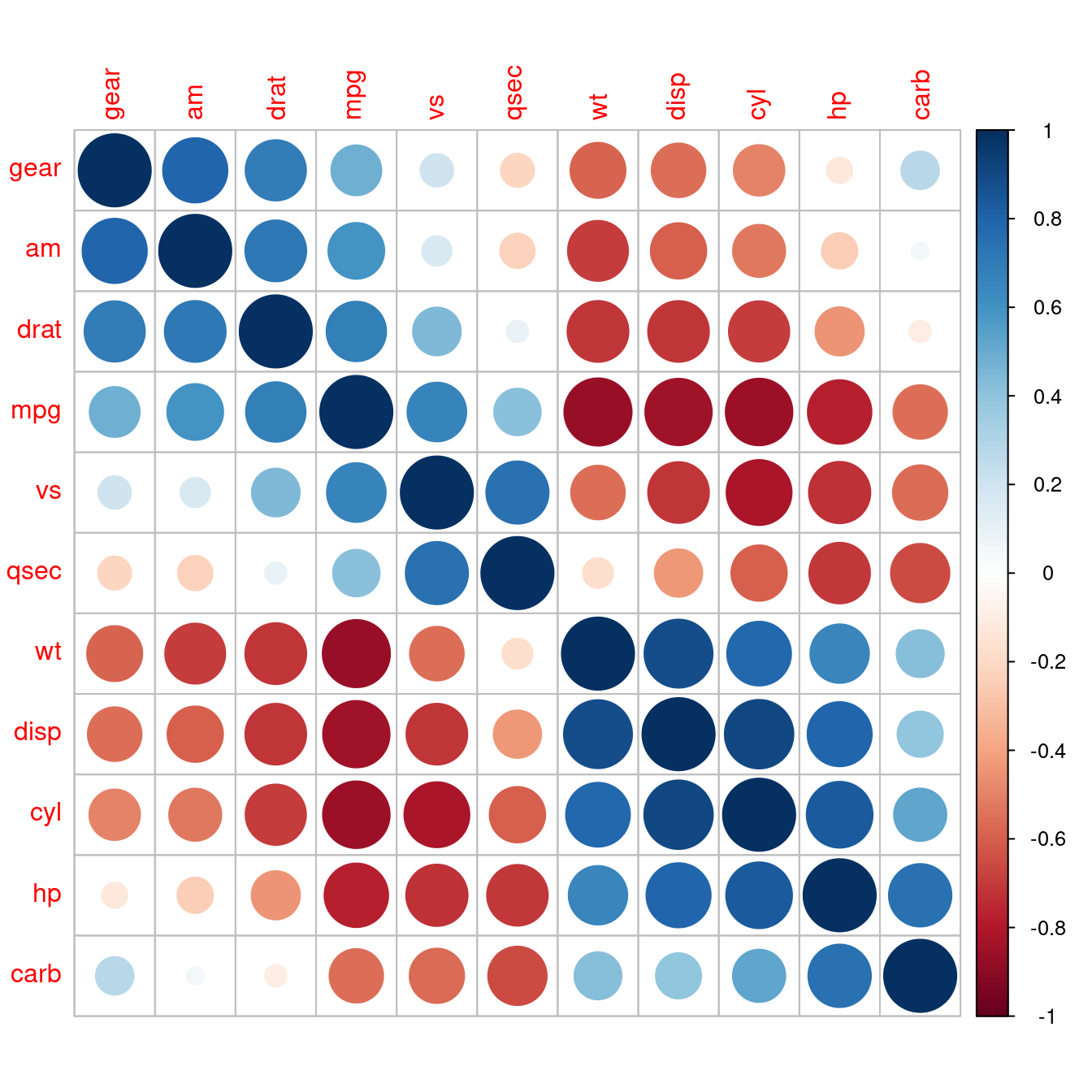
pimage(m)
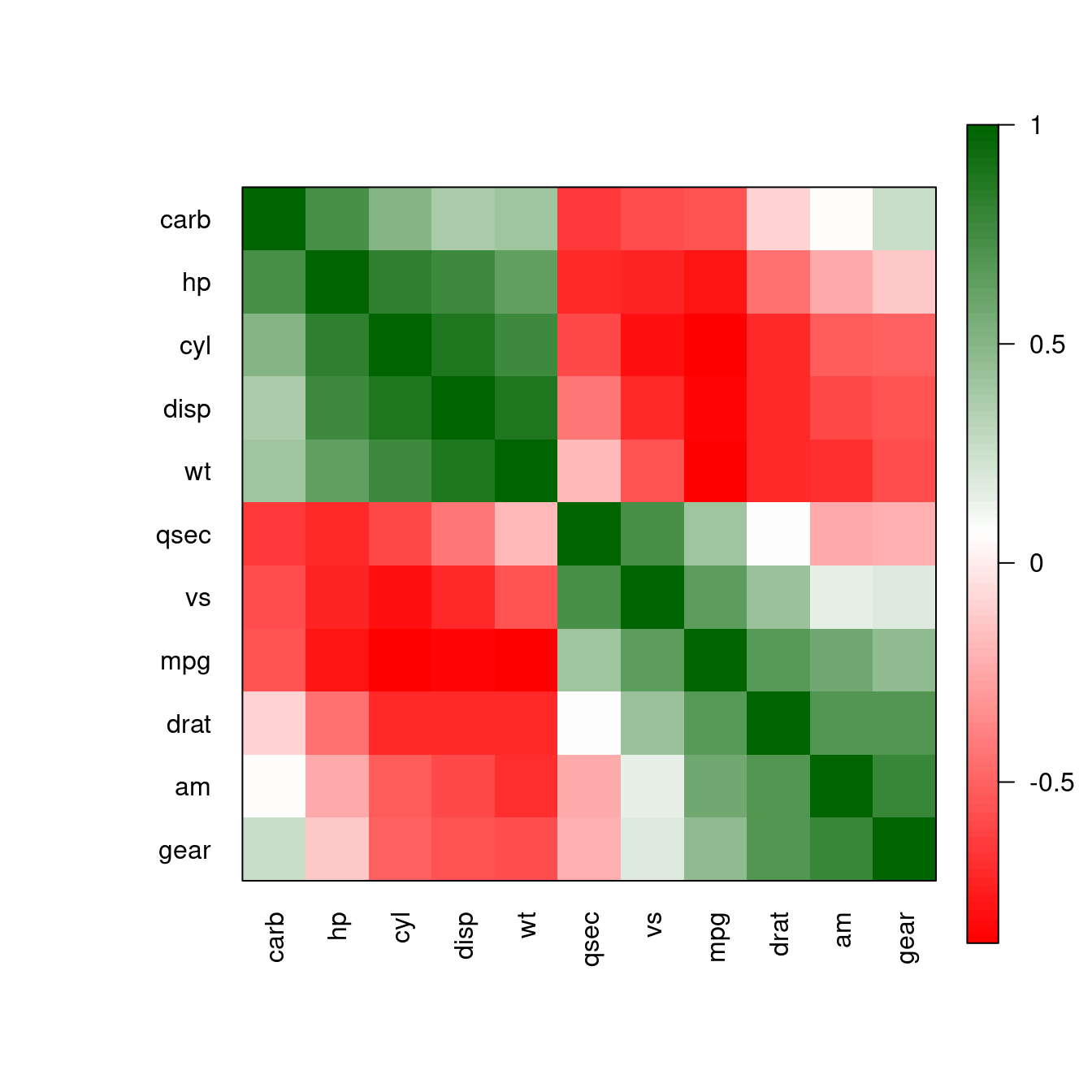
pimage(m, order = "AOE")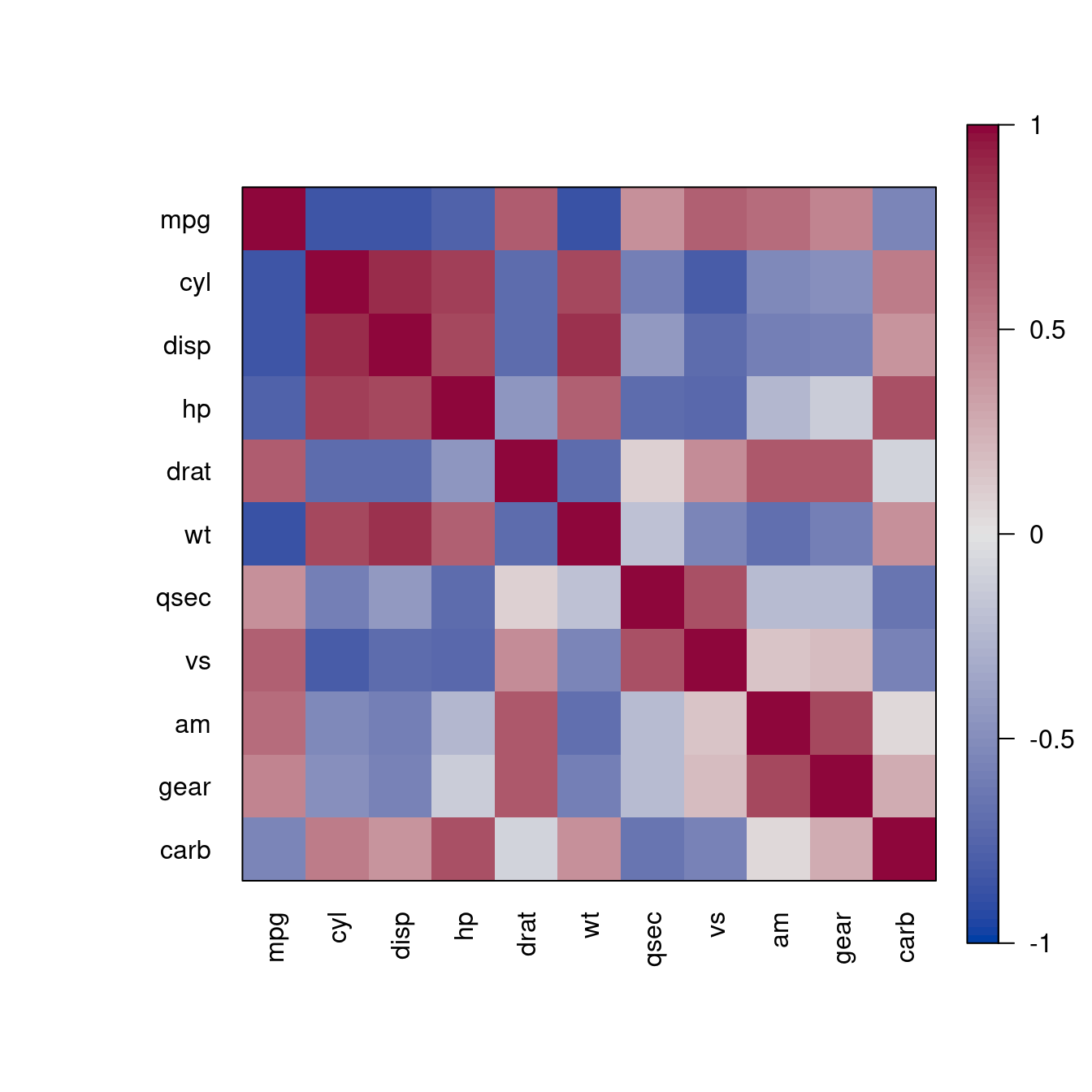

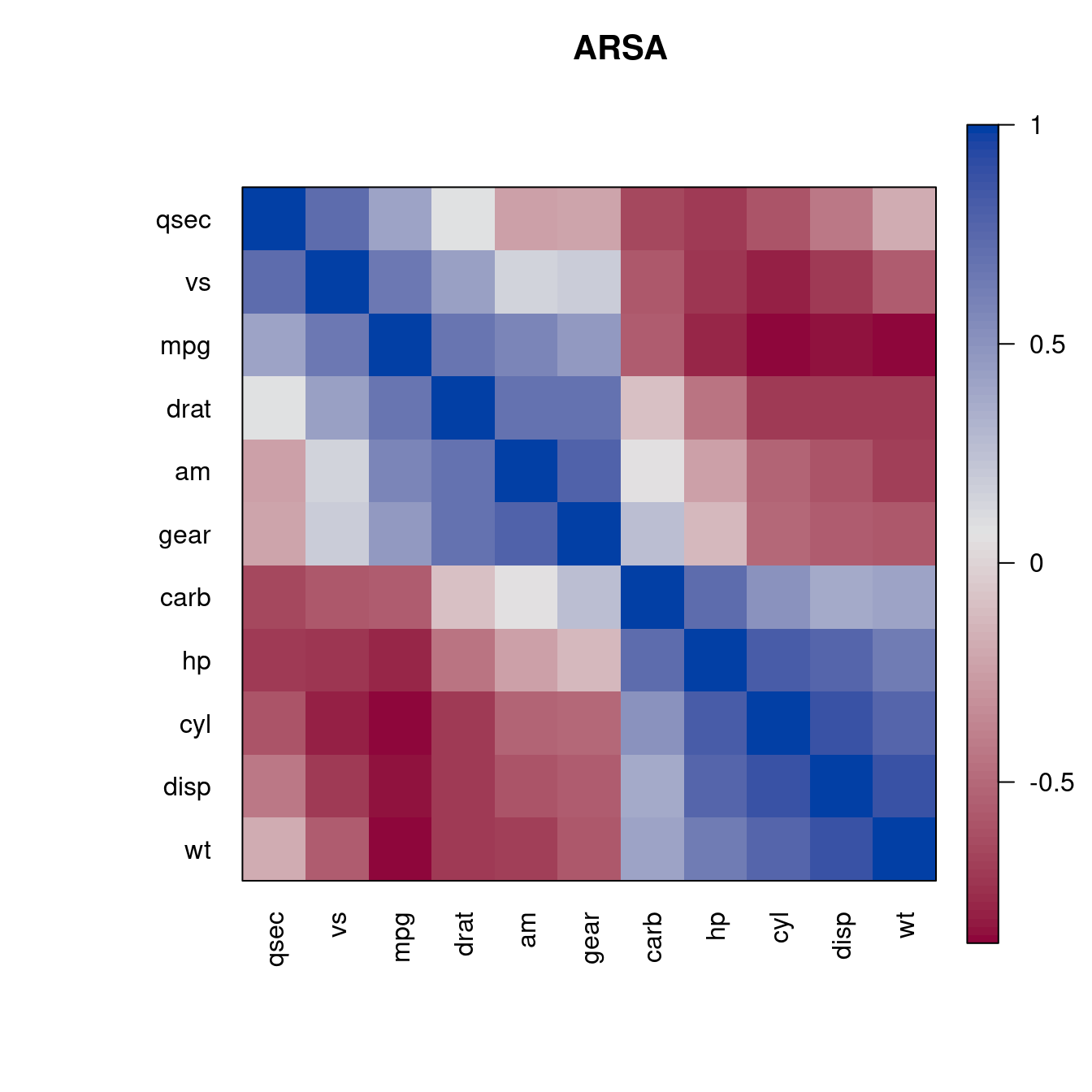
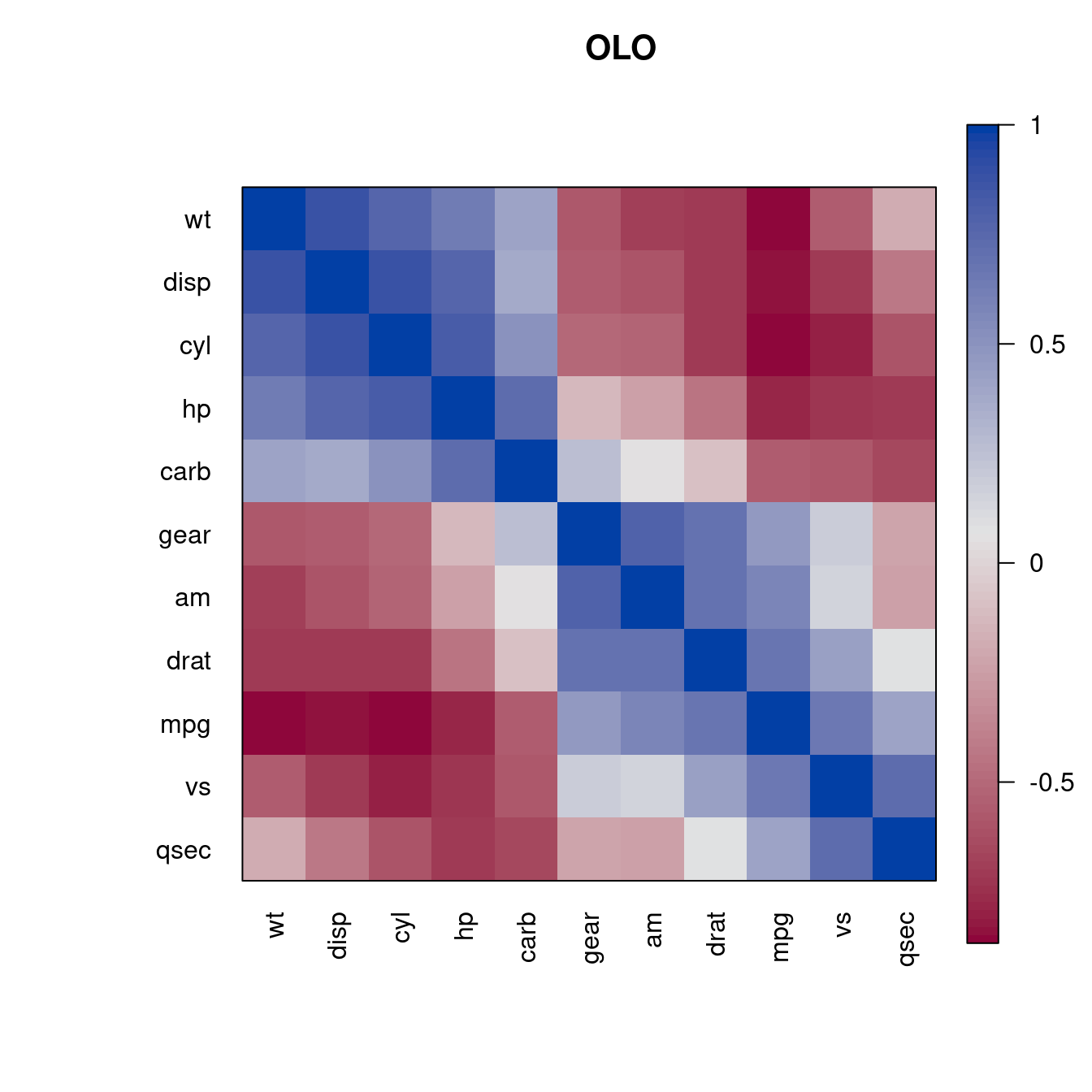
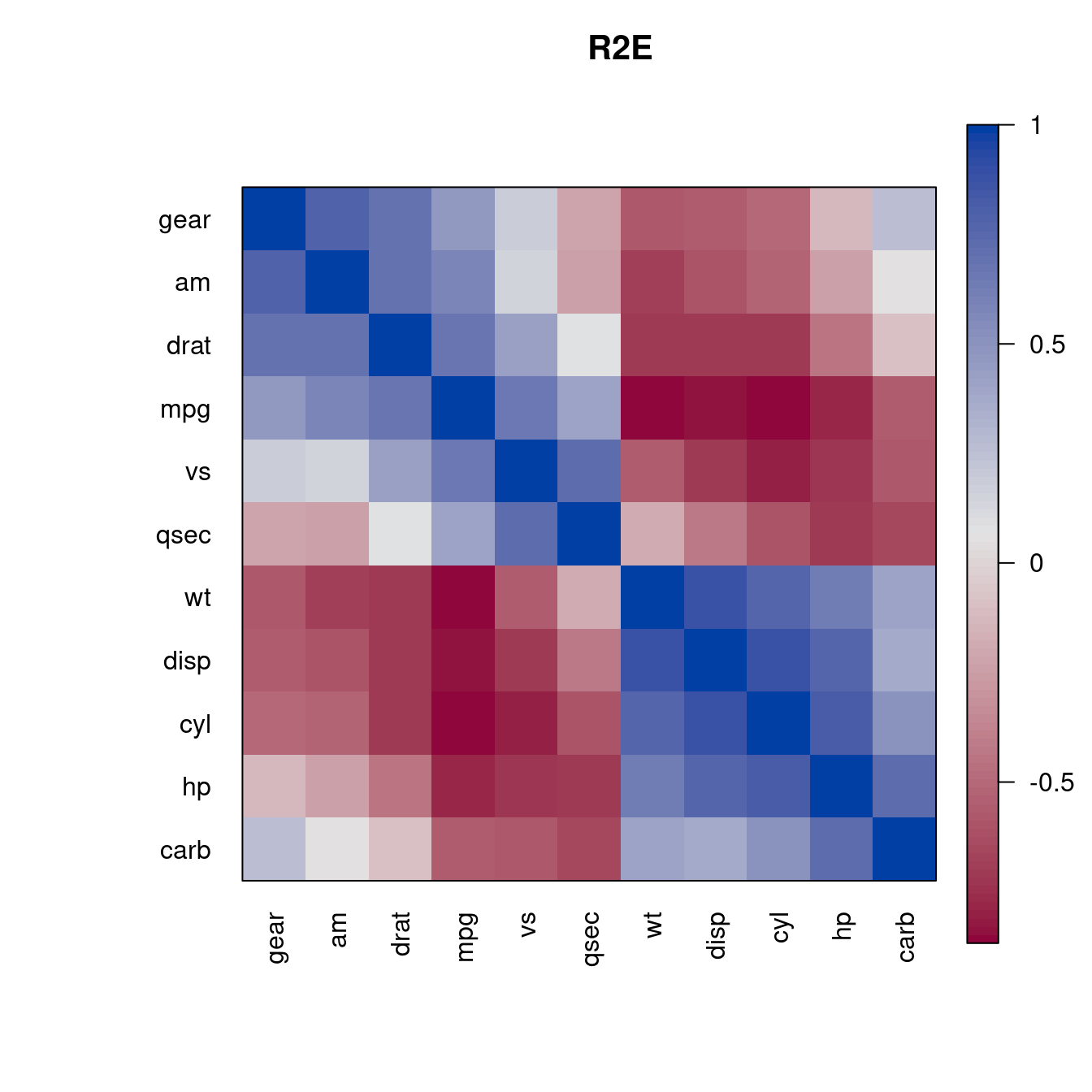
The reordering clearly shows that there is tow groups of highly correlated variables and these two groups have a strong negative correlation with each other.

Visualization options

Here are some options. Many packages represent high correlations as blue and low correlations as red. We can set the colors that way or used other colors.

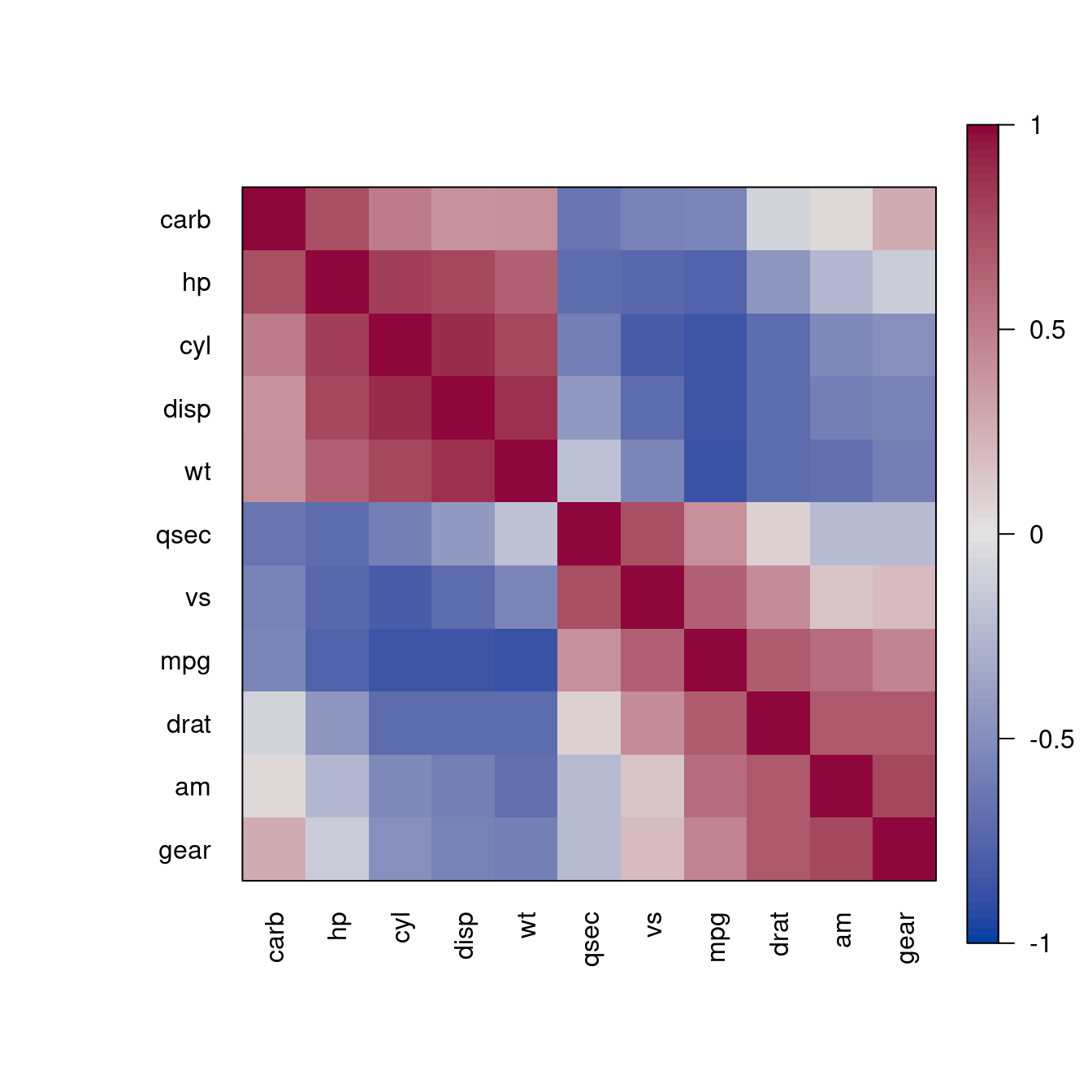
pimage(m, order = "AOE", col = rev(bluered()), diag = FALSE, upper_tri = FALSE)
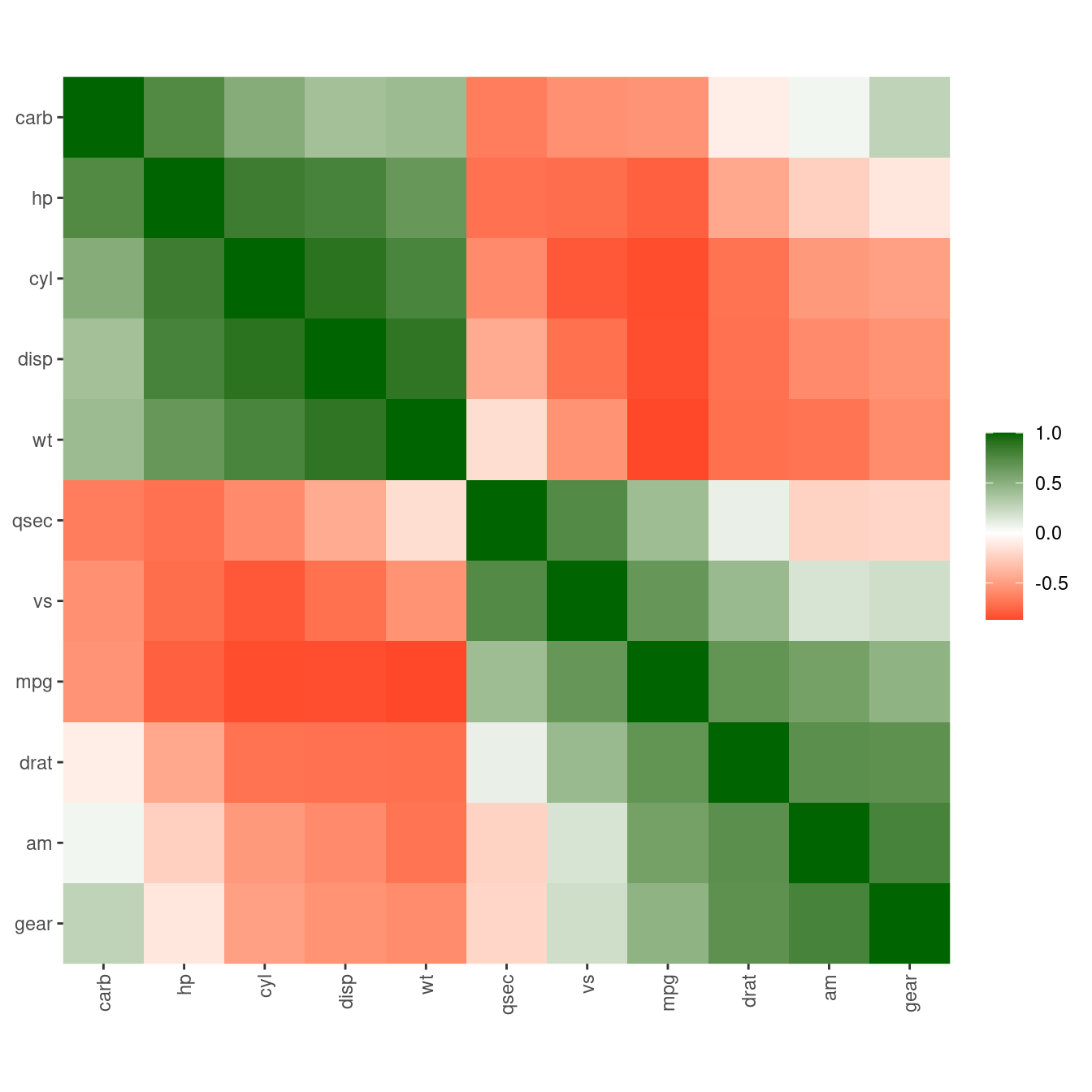
pimage(m, order = "AOE", col = colorRampPalette(c("red", "white", "darkgreen"))(100))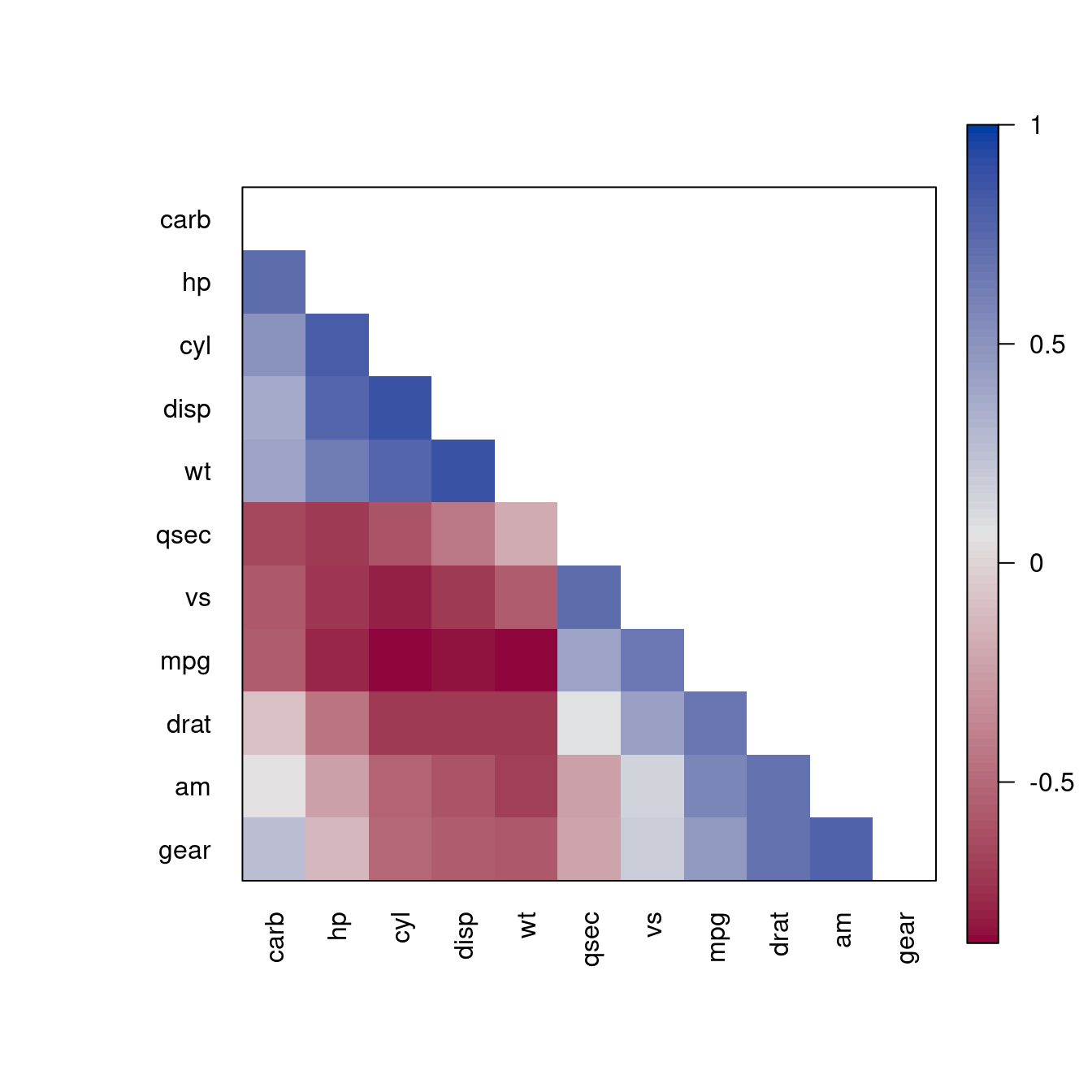

The plots are also available in ggplot2 versions.

library("ggplot2")

red_blue <- scale_fill_gradient2(
    low = scales::muted("red"),
    mid = "white",
    high = scales::muted("blue"),
    na.value = "white",
    midpoint = 0)

ggpimage(m, order = "AOE", diag = FALSE, upper_tri = FALSE) + red_blue
Scale for fill is already present.
Adding another scale for fill, which will replace the existing scale.
ggpimage(m, order = "AOE") + scale_fill_gradient2(low = "red", high = "darkgreen")
Scale for fill is already present.
Adding another scale for fill, which will replace the existing scale.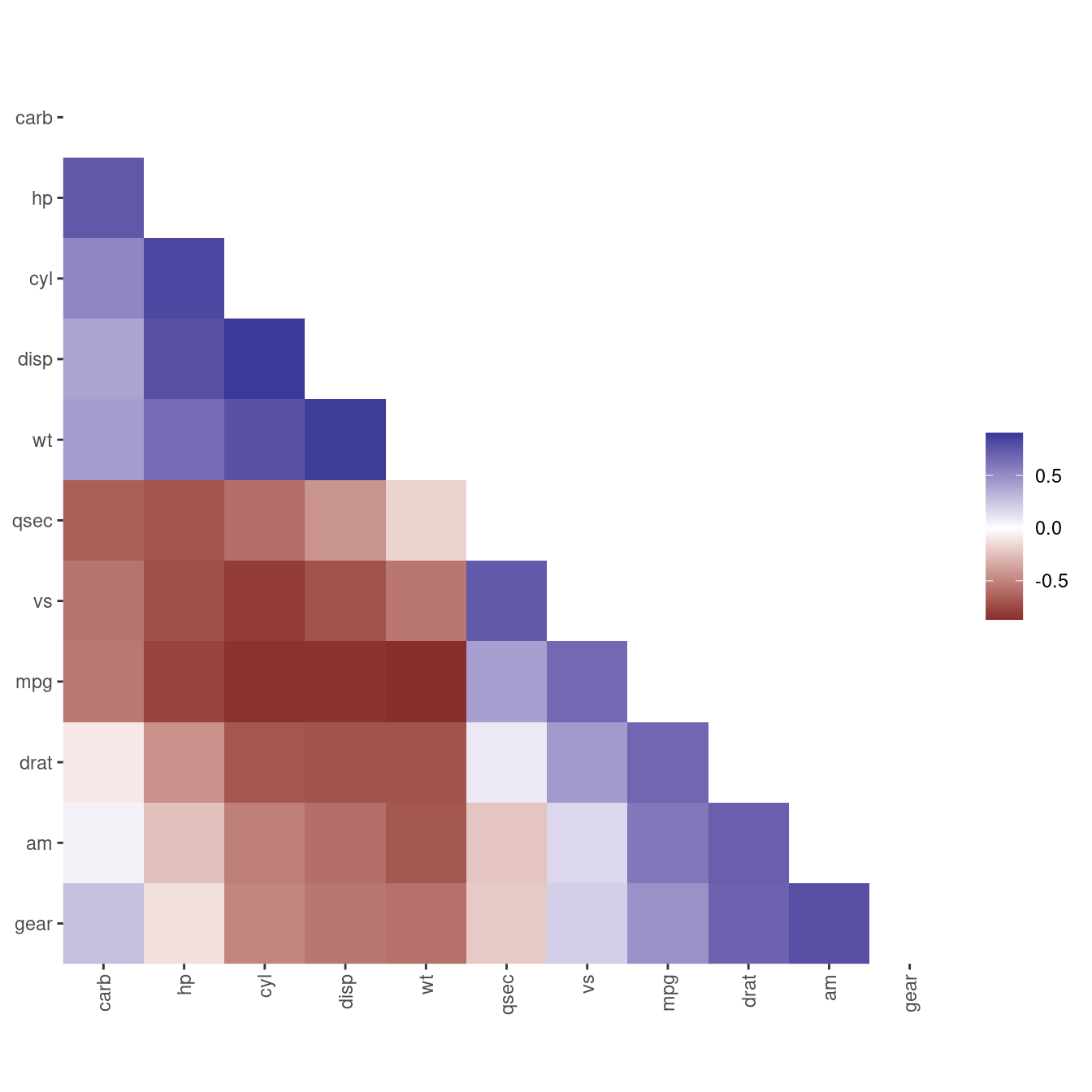

Using other seriation methods

We can apply any seriation method for distances to create an order. First, we convert the correlation matrix into a distance matrix using \(d_{ij} = \sqrt{1 - m_{ij}}\). Then we can use the distances for seriation and use the resulting order to rearrange the rows and columns of the correlation matrix.

d <- as.dist(sqrt(1 - m))

o <- seriate(d, "MDS")
pimage(m , order = c(o, o), main = "MDS", col = rev(bluered()))

o <- seriate(d, "ARSA")
pimage(m , order = c(o, o), main = "ARSA", col = rev(bluered()))

o <- seriate(d, "OLO")
pimage(m , order = c(o, o), main = "OLO", col = rev(bluered()))

o <- seriate(d, "R2E")
pimage(m , order = c(o, o), main = "R2E", col = rev(bluered()))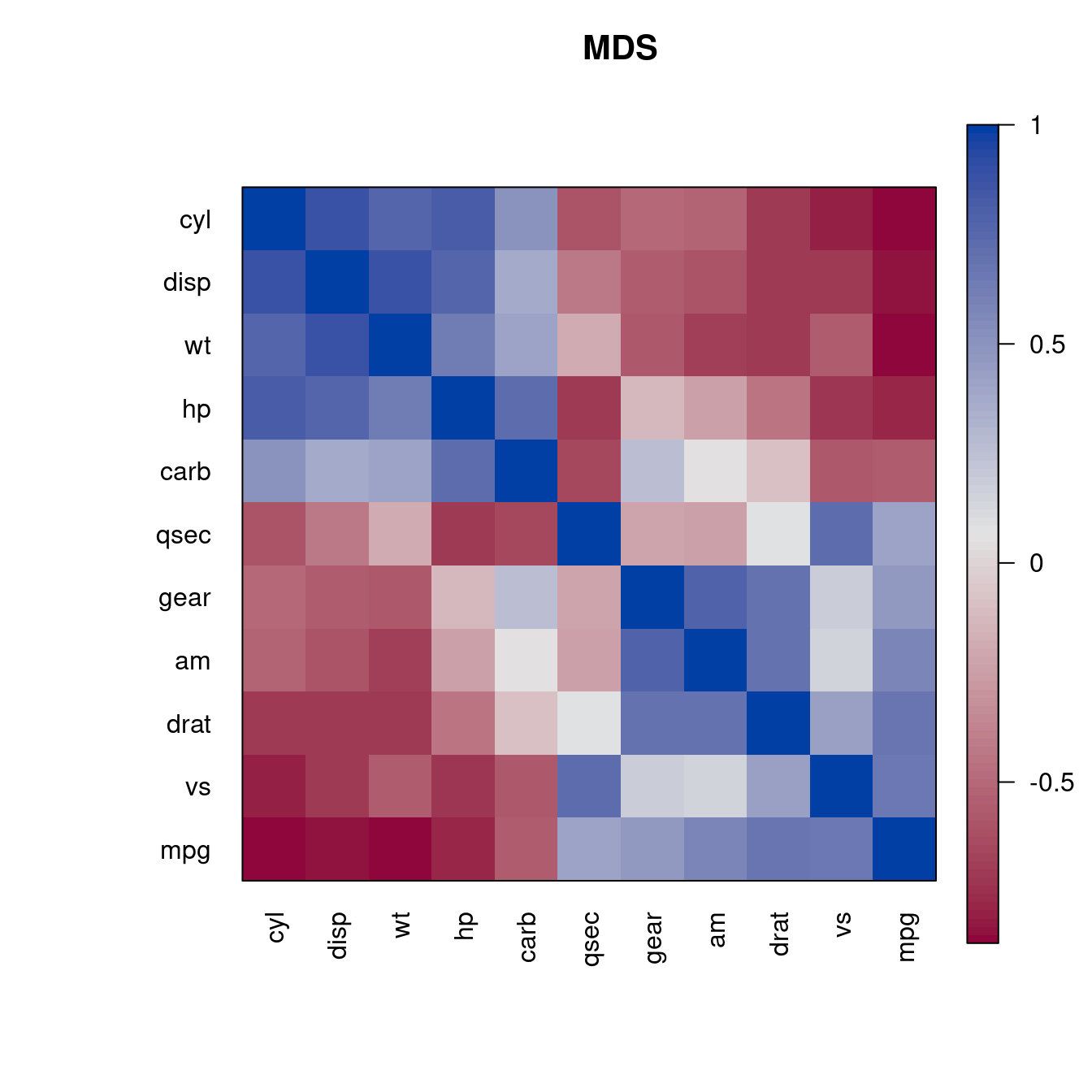

Other packages

Several other packages can be used to visualize and explore correlation structure. Some of these packages support reordering with the seriation package.

Package corrgram

The order argument in corrgram accepts methods from package seriation.

if (!require("corrgram")) install.packages("corrgram")
Loading required package: corrgram
library("corrgram")

corrgram(m, order = "OLO")
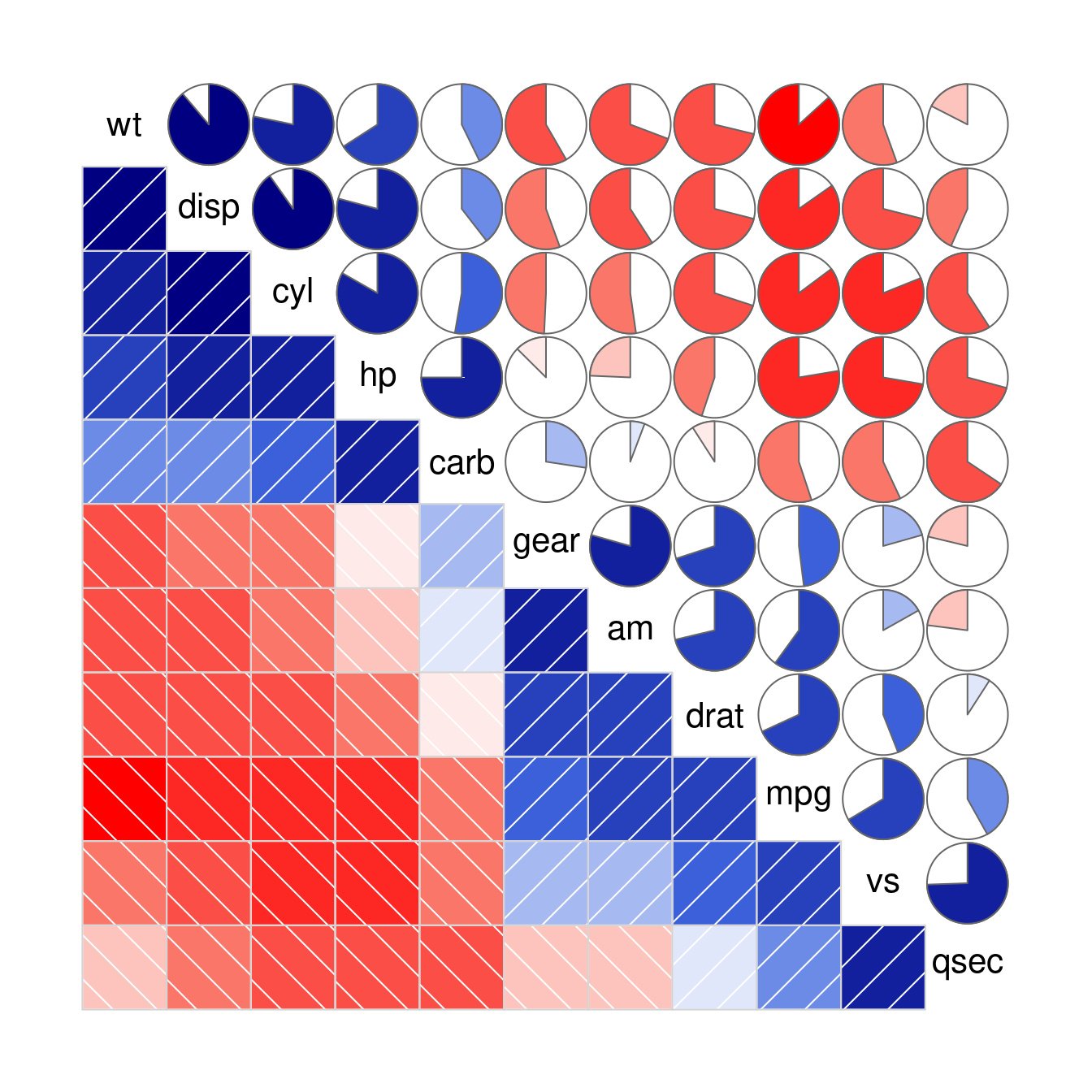
corrgram(m, order = "OLO", lower.panel=panel.shade, upper.panel=panel.pie)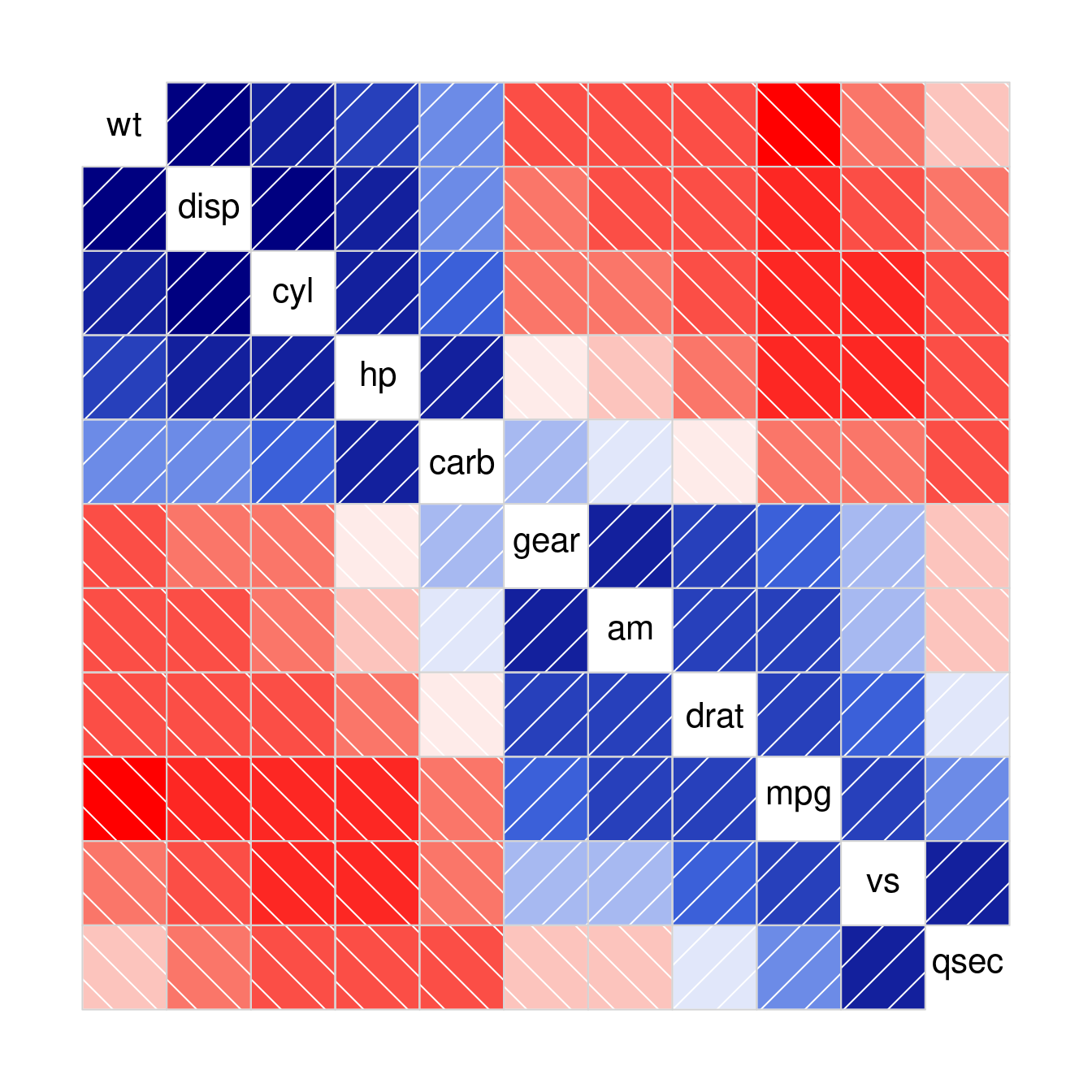

Package corrr

The function rearrange() in package corrr accepts some methods from seriation. Here is a complete example that uses method "R2E".

if (!require("corrr")) install.packages("corrr")
Loading required package: corrr
library("corrr")

x <- datasets::mtcars |>
       correlate() |>   
       focus(-cyl, -vs, mirror = TRUE) |>  # remove 'cyl' and 'vs'
       rearrange(method = "R2E") |>  
       shave()
Correlation computed with
• Method: 'pearson'
• Missing treated using: 'pairwise.complete.obs'
rplot(x)

Package corrplot

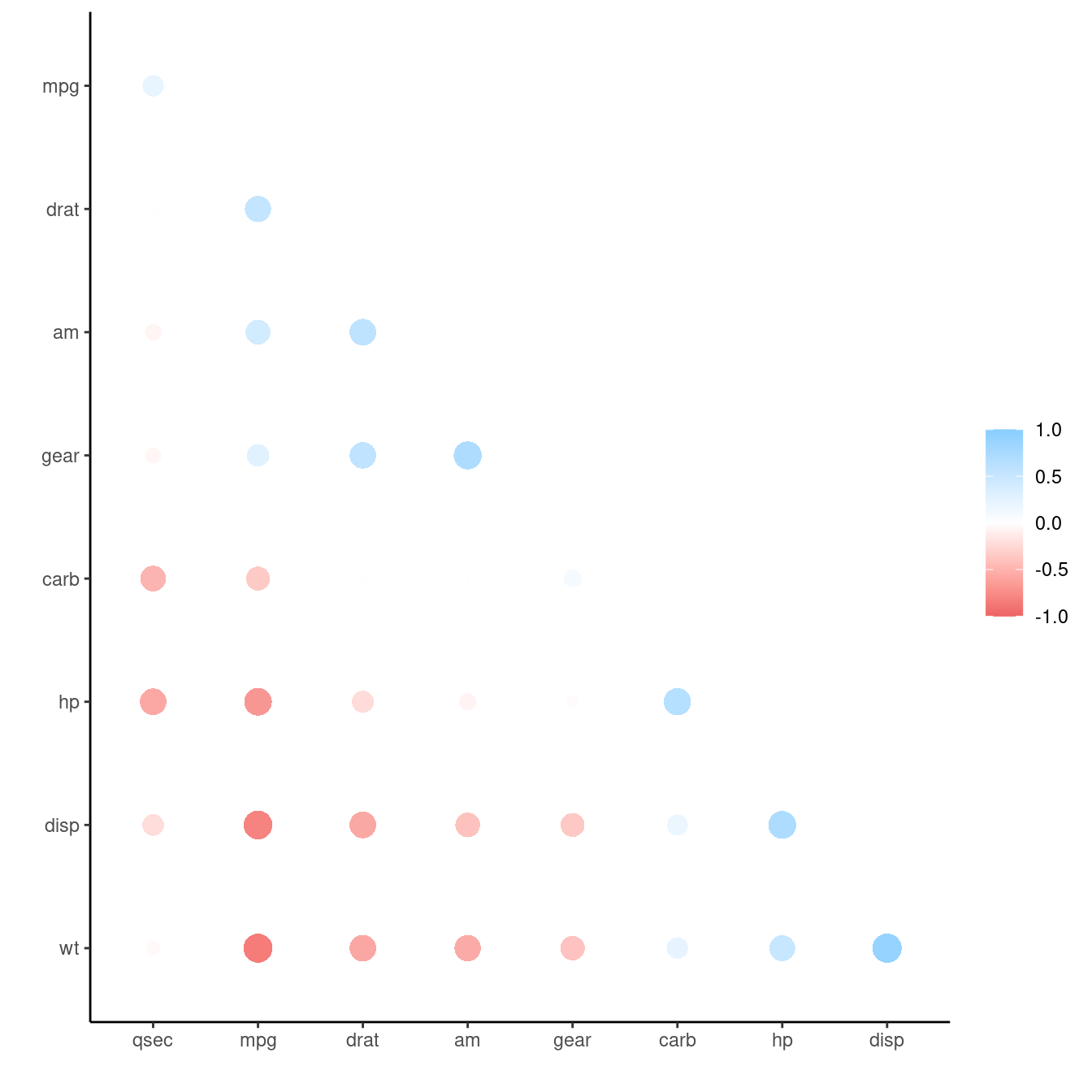
Package corrplot offers many visualization methods. Orders from package seriation can be used by permuting the correlation matrix before it is passed to corrplot().

if (!require("corrplot")) install.packages("corrplot")
Loading required package: corrplot
corrplot 0.92 loaded
library("corrplot")

d <- as.dist(sqrt(1 - m))
o <- seriate(d, "R2E")
m_R2E <- permute(m, c(o,o))

corrplot(m_R2E , order = "original")

References