7 Clustering Analysis

pkgs <- sort(c('tidyverse', 'factoextra', 'dbscan', 'cluster', 'mclust', 
  'kernlab', 'e1071', 'scatterpie', 'fpc', 'seriation', 'mlbench', 'GGally'
))
  
pkgs_install <- pkgs[!(pkgs %in% installed.packages()[,"Package"])]
if(length(pkgs_install)) install.packages(pkgs_install)

The packages used for this chapter are: cluster (Maechler et al. 2022), dbscan (Hahsler and Piekenbrock 2023), e1071 (Meyer et al. 2023), factoextra (Kassambara and Mundt 2020), fpc (Hennig 2023), GGally (Schloerke et al. 2021), kernlab (Karatzoglou, Smola, and Hornik 2023), mclust (Fraley, Raftery, and Scrucca 2022), mlbench (Leisch and Dimitriadou. 2023), scatterpie (Yu 2023), seriation (Hahsler, Buchta, and Hornik 2023), tidyverse (Wickham 2023 b)

7.1 Introduction

Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters).

Clustering is also called unsupervised learning, because it tries to directly learns the structure of the data and does not rely on the availability of a correct answer or class label as supervised learning does. Clustering is often used for exploratory analysis or to preprocess data by grouping.

You can read the free sample chapter from the textbook (Tan, Steinbach, and Kumar 2005): Chapter 7. Cluster Analysis: Basic Concepts and Algorithms

7.2 Data Preparation

library(tidyverse)

We will use here a small and very clean toy dataset called Ruspini which is included in the R package cluster.

data(ruspini, package = "cluster")

The Ruspini data set, consisting of 75 points in four groups that is popular for illustrating clustering techniques. It is a very simple data set with well separated clusters. The original dataset has the points ordered by group. We can shuffle the data (rows) using sample_frac which samples by default 100%.

ruspini <- as_tibble(ruspini) |> 
  sample_frac()
ruspini

## # A tibble: 75 × 2
##        x     y
##    <int> <int>
##  1   115   117
##  2   111   126
##  3    85    96
##  4    12    88
##  5    36    72
##  6    28   147
##  7    24    58
##  8    99   128
##  9    46   142
## 10    38   151
## # ℹ 65 more rows

7.2.1 Data cleaning

ggplot(ruspini, aes(x = x, y = y)) + geom_point()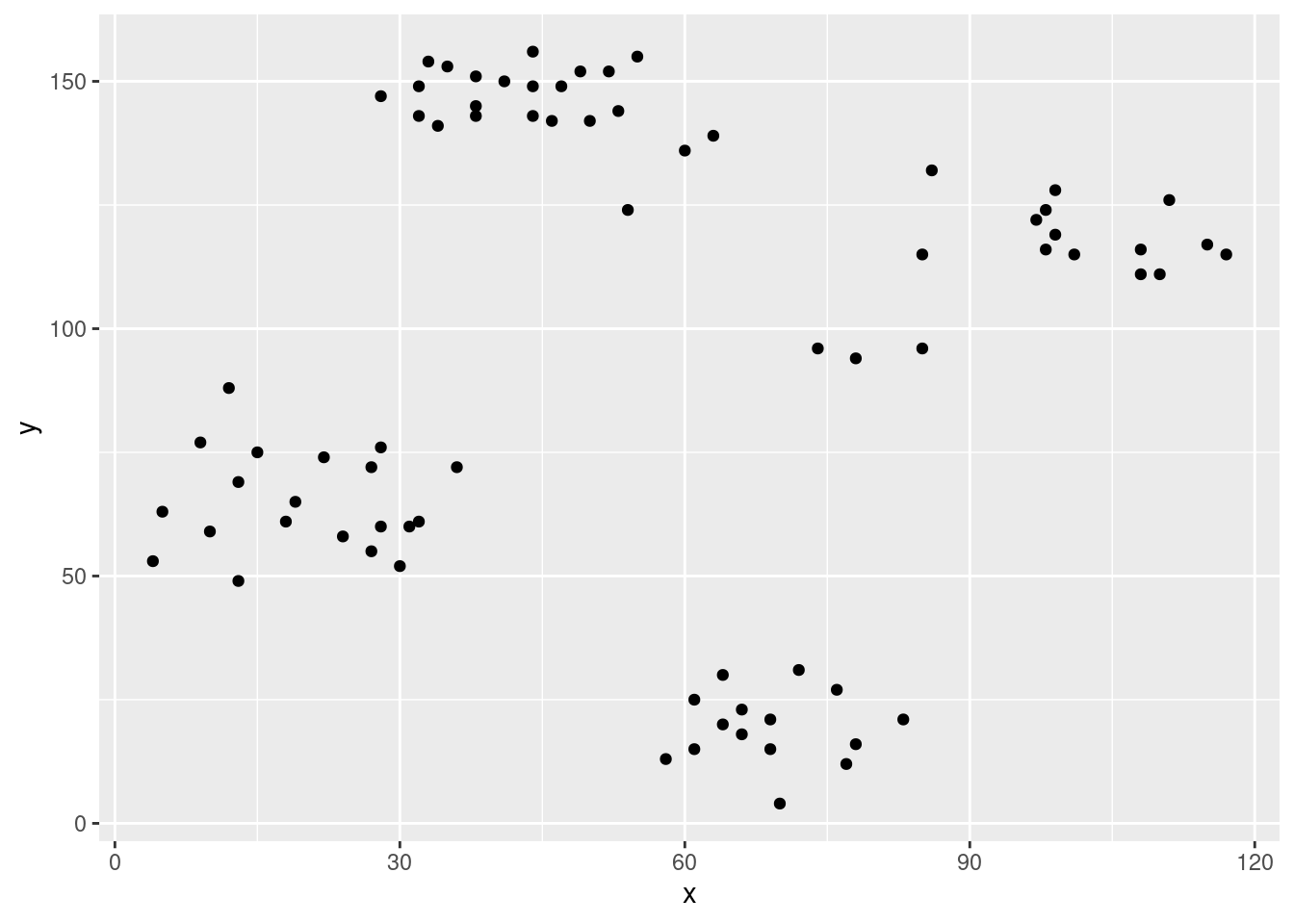

summary(ruspini)

##        x               y        
##  Min.   :  4.0   Min.   :  4.0  
##  1st Qu.: 31.5   1st Qu.: 56.5  
##  Median : 52.0   Median : 96.0  
##  Mean   : 54.9   Mean   : 92.0  
##  3rd Qu.: 76.5   3rd Qu.:141.5  
##  Max.   :117.0   Max.   :156.0

For most clustering algorithms it is necessary to handle missing values and outliers (e.g., remove the observations). For details see Section “Outlier removal” below. This data set has not missing values or strong outlier and looks like it has some very clear groups.

7.2.2 Scale data

Clustering algorithms use distances and the variables with the largest number range will dominate distance calculation. The summary above shows that this is not an issue for the Ruspini dataset with both, x and y, being roughly between 0 and 150. Most data analysts will still scale each column in the data to zero mean and unit standard deviation (z-scores). Note: The standard scale() function scales a whole data matrix so we implement a function for a single vector and apply it to all numeric columns.

## I use this till tidyverse implements a scale function
scale_numeric <- function(x) mutate_if(x, is.numeric, function(y) as.vector(scale(y)))

ruspini_scaled <- ruspini |> 
  scale_numeric()
summary(ruspini_scaled)

##        x                y         
##  Min.   :-1.668   Min.   :-1.807  
##  1st Qu.:-0.766   1st Qu.:-0.729  
##  Median :-0.094   Median : 0.082  
##  Mean   : 0.000   Mean   : 0.000  
##  3rd Qu.: 0.709   3rd Qu.: 1.016  
##  Max.   : 2.037   Max.   : 1.314

After scaling, most z-scores will fall in the range $[-3,3]$ (z-scores are measured in standard deviations from the mean), where $0$ means average.

7.3 Clustering methods

7.3.1 k-means Clustering

k-means implicitly assumes Euclidean distances. We use $k = 4$ clusters and run the algorithm 10 times with random initialized centroids. The best result is returned.

km <- kmeans(ruspini_scaled, centers = 4, nstart = 10)
km

## K-means clustering with 4 clusters of sizes 23, 17, 15, 20
## 
## Cluster means:
##        x      y
## 1 -0.360  1.109
## 2  1.419  0.469
## 3  0.461 -1.491
## 4 -1.139 -0.556
## 
## Clustering vector:
##  [1] 2 2 2 4 4 1 4 2 1 1 1 1 4 3 3 2 4 3 2 1 1 1 2 2 3
## [26] 2 1 3 3 2 1 3 3 4 2 1 3 4 4 3 1 4 1 3 2 4 3 1 2 1
## [51] 1 2 2 4 4 2 1 4 3 4 1 1 2 4 4 4 1 1 3 3 4 1 1 4 4
## 
## Within cluster sum of squares by cluster:
## [1] 2.66 3.64 1.08 2.71
##  (between_SS / total_SS =  93.2 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"       
## [4] "withinss"     "tot.withinss" "betweenss"   
## [7] "size"         "iter"         "ifault"

km is an R object implemented as a list. The clustering vector contains the cluster assignment for each data row and can be accessed using km$cluster. I add the cluster assignment as a column to the scaled dataset (I make it a factor since it represents a nominal label).

ruspini_clustered <- ruspini_scaled |> add_column(cluster = factor(km$cluster))
ruspini_clustered

## # A tibble: 75 × 3
##         x       y cluster
##     <dbl>   <dbl> <fct>  
##  1  1.97   0.513  2      
##  2  1.84   0.698  2      
##  3  0.987  0.0816 2      
##  4 -1.41  -0.0827 4      
##  5 -0.619 -0.411  4      
##  6 -0.881  1.13   1      
##  7 -1.01  -0.699  4      
##  8  1.45   0.739  2      
##  9 -0.291  1.03   1      
## 10 -0.553  1.21   1      
## # ℹ 65 more rows

ggplot(ruspini_clustered, aes(x = x, y = y, color = cluster)) + geom_point()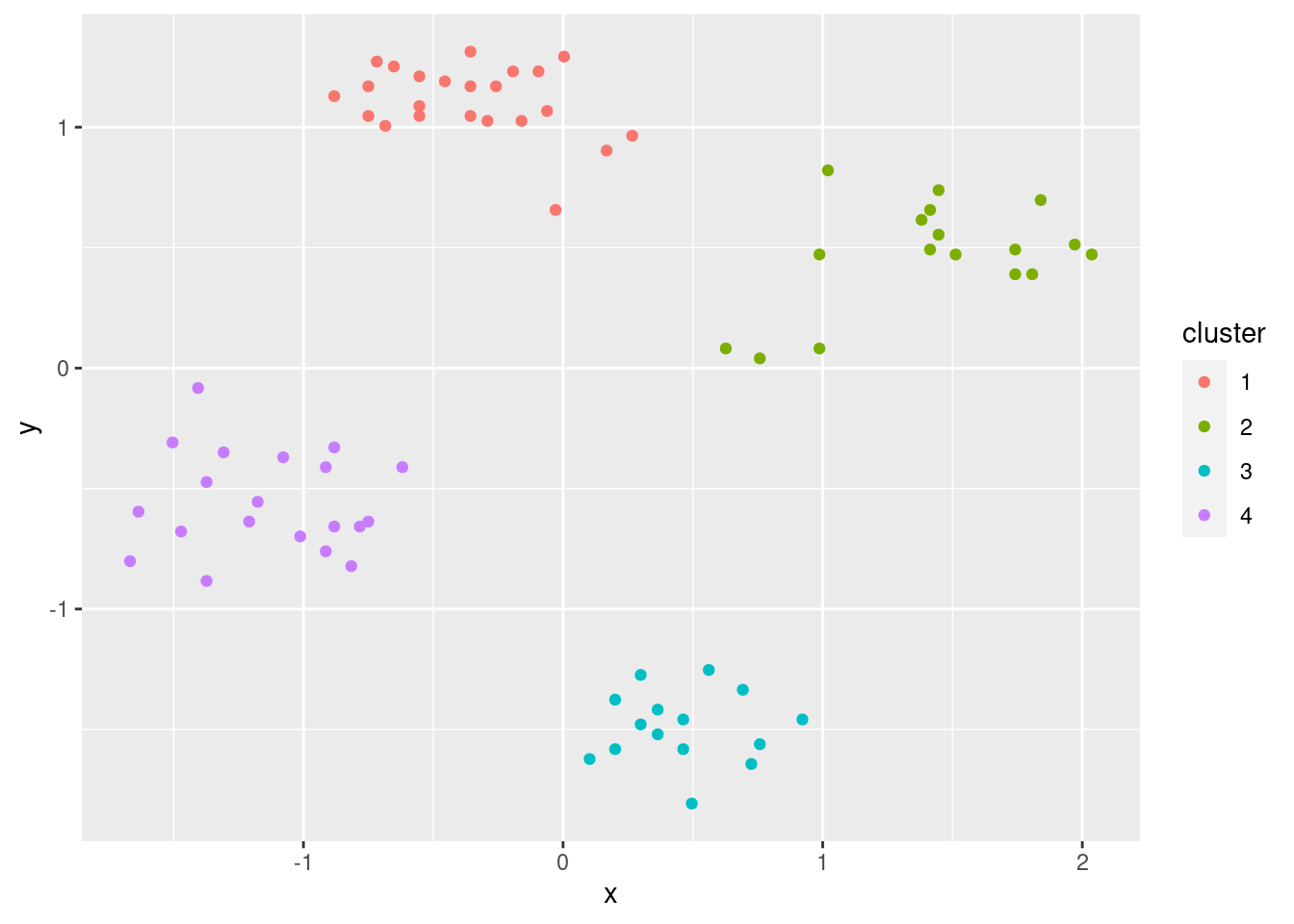

Add the centroids to the plot.

centroids <- as_tibble(km$centers, rownames = "cluster")
centroids

## # A tibble: 4 × 3
##   cluster      x      y
##   <chr>    <dbl>  <dbl>
## 1 1       -0.360  1.11 
## 2 2        1.42   0.469
## 3 3        0.461 -1.49 
## 4 4       -1.14  -0.556

ggplot(ruspini_clustered, aes(x = x, y = y, color = cluster)) + geom_point() +
  geom_point(data = centroids, aes(x = x, y = y, color = cluster), shape = 3, size = 10)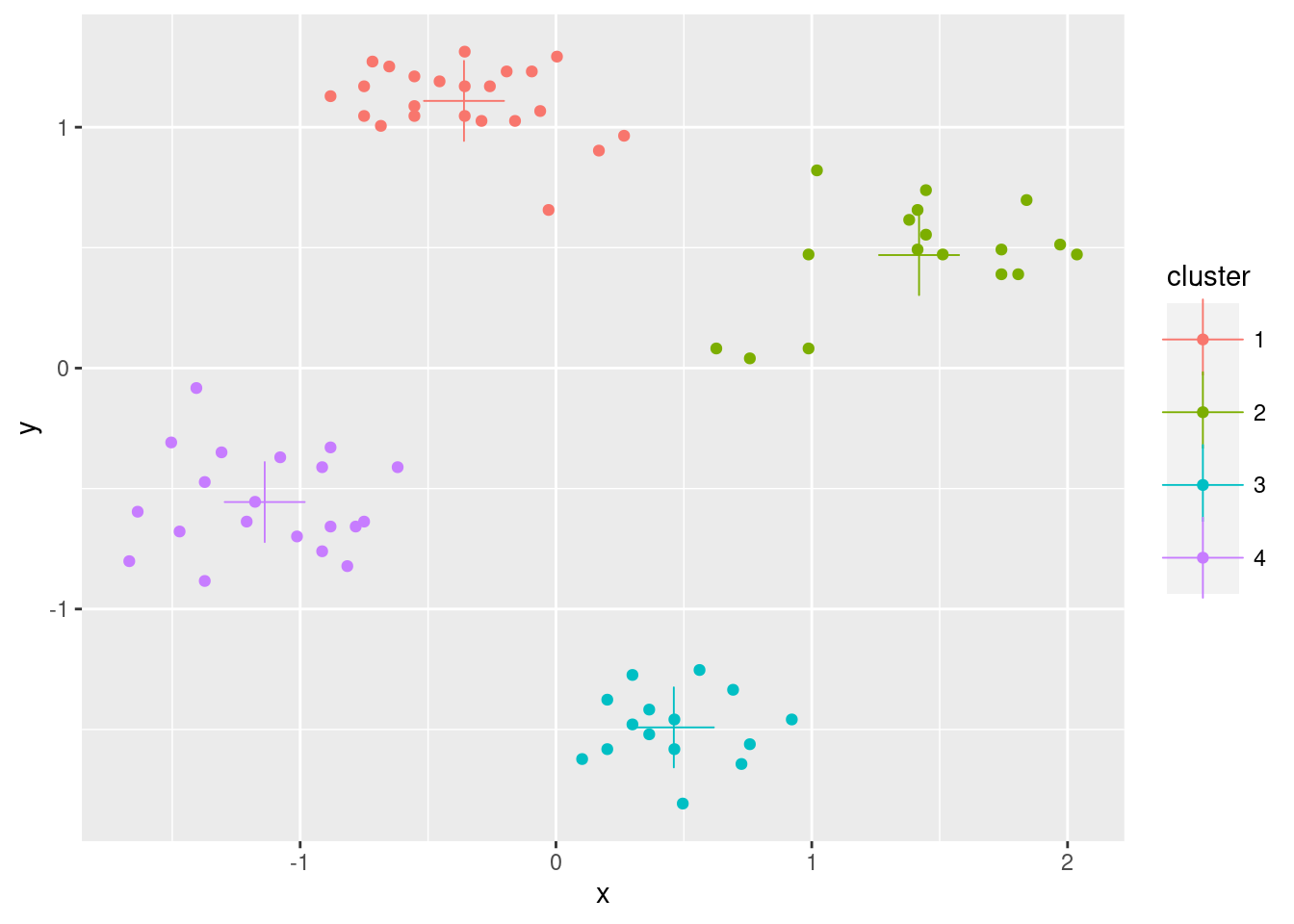

Use the factoextra package for visualization

library(factoextra)
fviz_cluster(km, data = ruspini_scaled, centroids = TRUE, repel = TRUE, ellipse.type = "norm")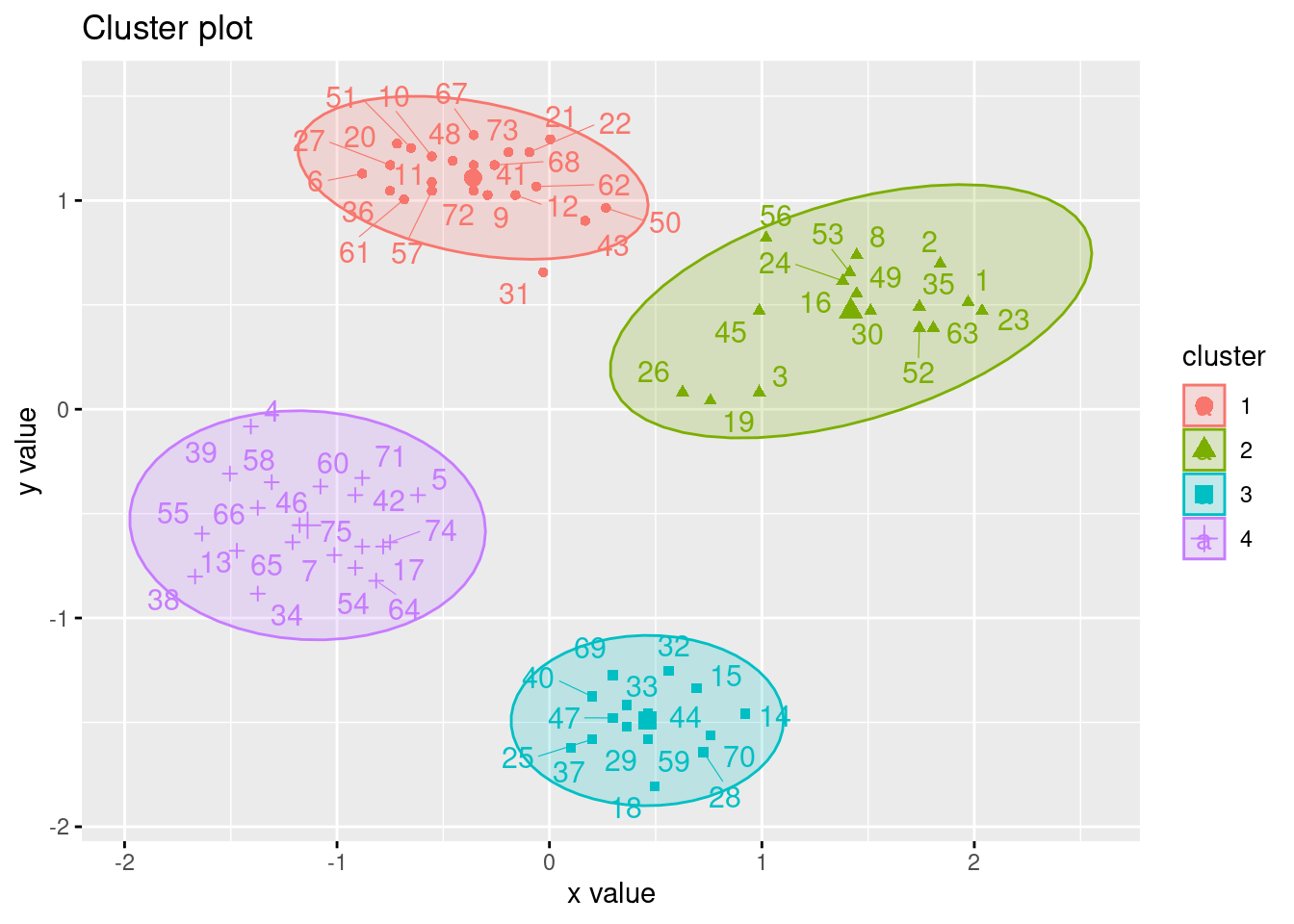

7.3.1.1 Inspect clusters

We inspect the clusters created by the 4-cluster k-means solution. The following code can be adapted to be used for other clustering methods.

7.3.1.1.1 Cluster Profiles

Inspect the centroids with horizontal bar charts organized by cluster. To group the plots by cluster, we have to change the data format to the “long”-format using a pivot operation. I use colors to match the clusters in the scatter plots.

ggplot(pivot_longer(centroids, cols = c(x, y), names_to = "feature"),
  aes(x = value, y = feature, fill = cluster)) +
  geom_bar(stat = "identity") +
  facet_grid(rows = vars(cluster))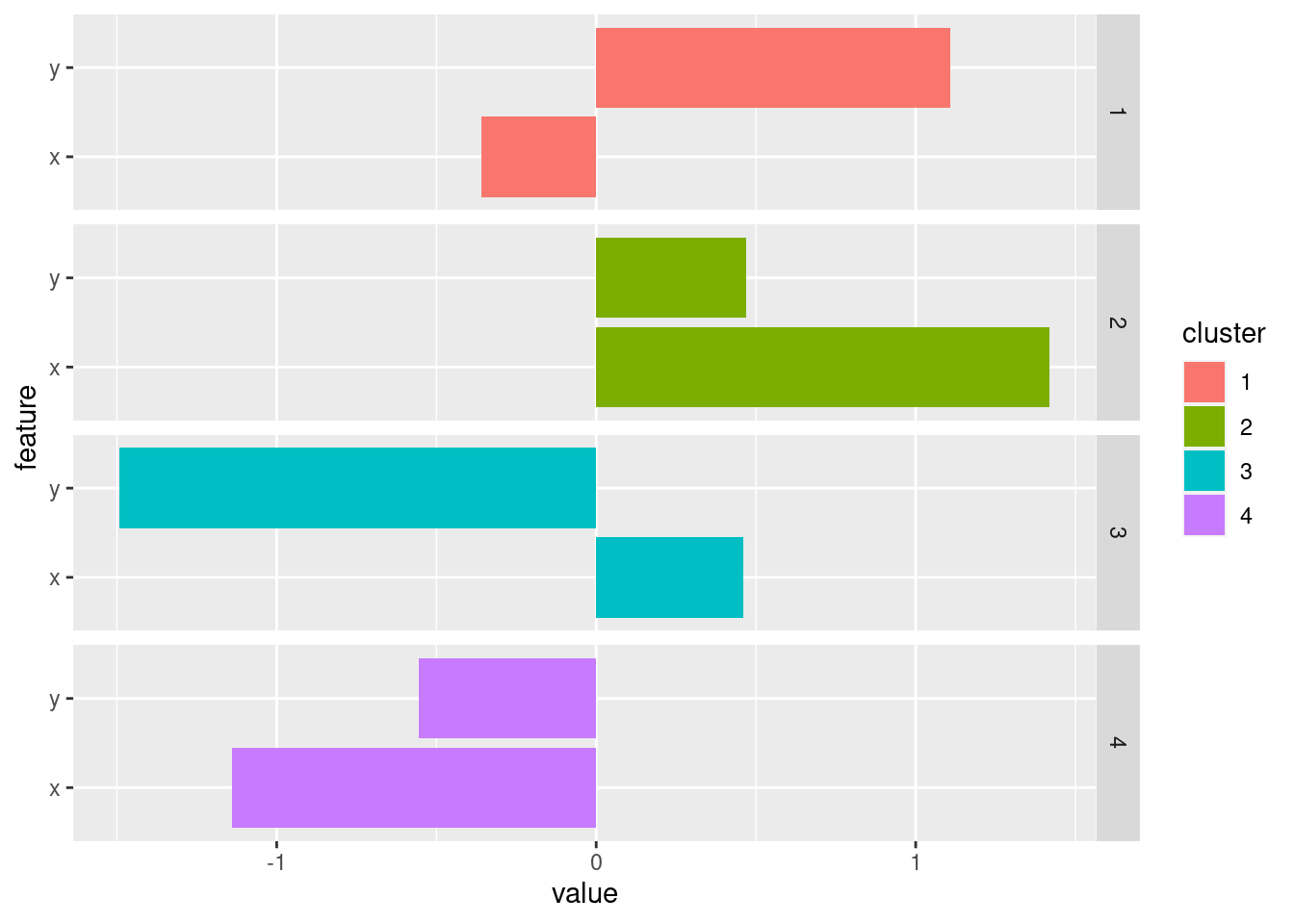

7.3.1.1.2 Extract a single cluster

You need is to filter the rows corresponding to the cluster index. The next example calculates summary statistics and then plots all data points of cluster 1.

cluster1 <- ruspini_clustered |> 
  filter(cluster == 1)
cluster1

## # A tibble: 23 × 3
##           x     y cluster
##       <dbl> <dbl> <fct>  
##  1 -0.881   1.13  1      
##  2 -0.291   1.03  1      
##  3 -0.553   1.21  1      
##  4 -0.553   1.09  1      
##  5 -0.160   1.03  1      
##  6 -0.717   1.27  1      
##  7  0.00393 1.29  1      
##  8 -0.0944  1.23  1      
##  9 -0.750   1.17  1      
## 10 -0.0289  0.657 1      
## # ℹ 13 more rows

summary(cluster1)

##        x                y         cluster
##  Min.   :-0.881   Min.   :0.657   1:23   
##  1st Qu.:-0.603   1st Qu.:1.036   2: 0   
##  Median :-0.357   Median :1.129   3: 0   
##  Mean   :-0.360   Mean   :1.109   4: 0   
##  3rd Qu.:-0.127   3rd Qu.:1.221          
##  Max.   : 0.266   Max.   :1.314

ggplot(cluster1, aes(x = x, y = y)) + geom_point() +
  coord_cartesian(xlim = c(-2, 2), ylim = c(-2, 2))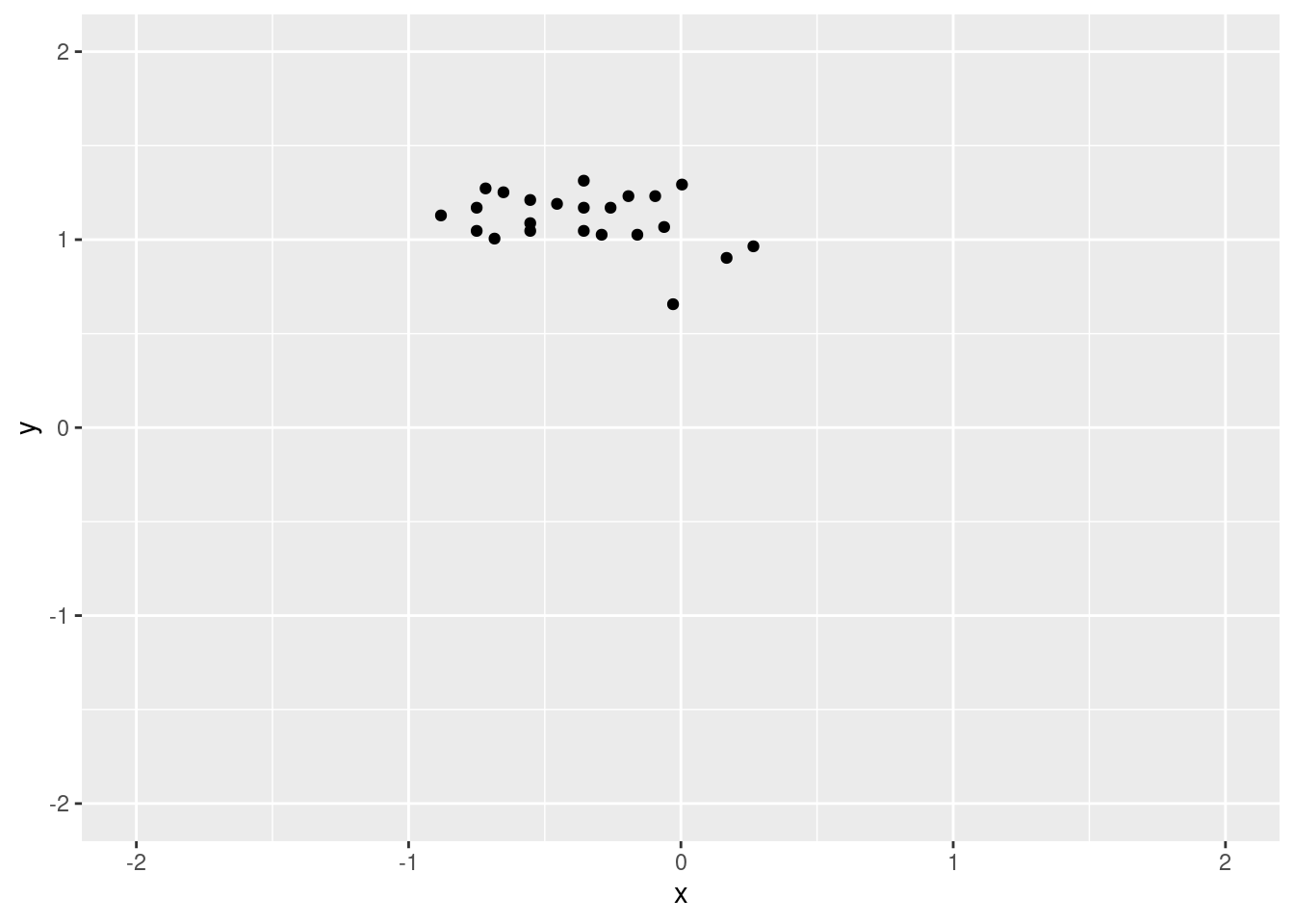

What happens if we try to cluster with 8 centers?

fviz_cluster(kmeans(ruspini_scaled, centers = 8), data = ruspini_scaled,
  centroids = TRUE,  geom = "point", ellipse.type = "norm")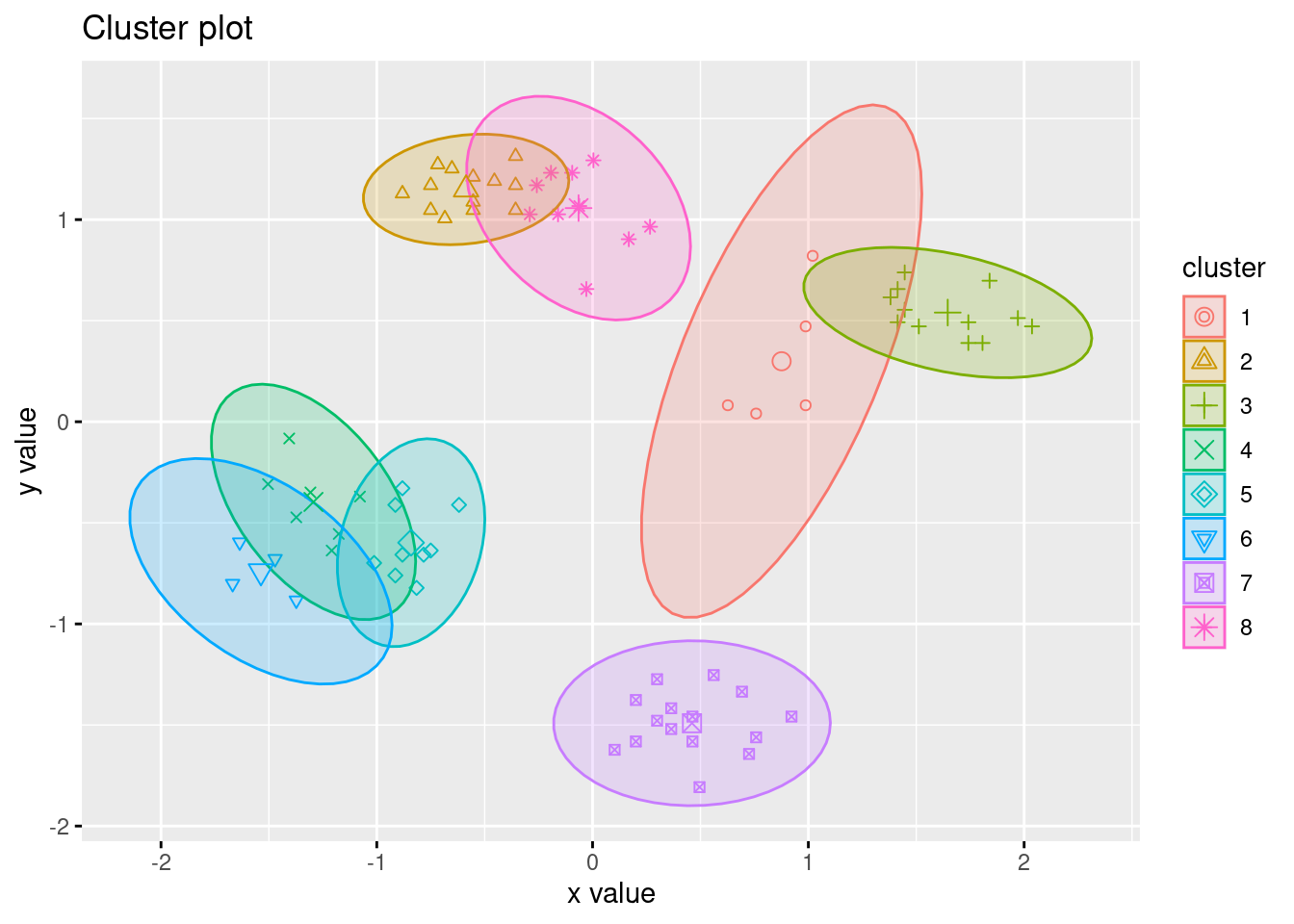

7.3.2 Hierarchical Clustering

Hierarchical clustering starts with a distance matrix. dist() defaults to method=“Euclidean”. Note: Distance matrices become very large quickly (size and time complexity is $O(n^2)$ where $n$ is the number if data points). It is only possible to calculate and store the matrix for small data sets (maybe a few hundred thousand data points) in main memory. If your data is too large then you can use sampling.

d <- dist(ruspini_scaled)

hclust() implements agglomerative hierarchical clustering. We cluster using complete link.

hc <- hclust(d, method = "complete")

Hierarchical clustering does not return cluster assignments but a dendrogram. The standard plot function plots the dendrogram.

plot(hc)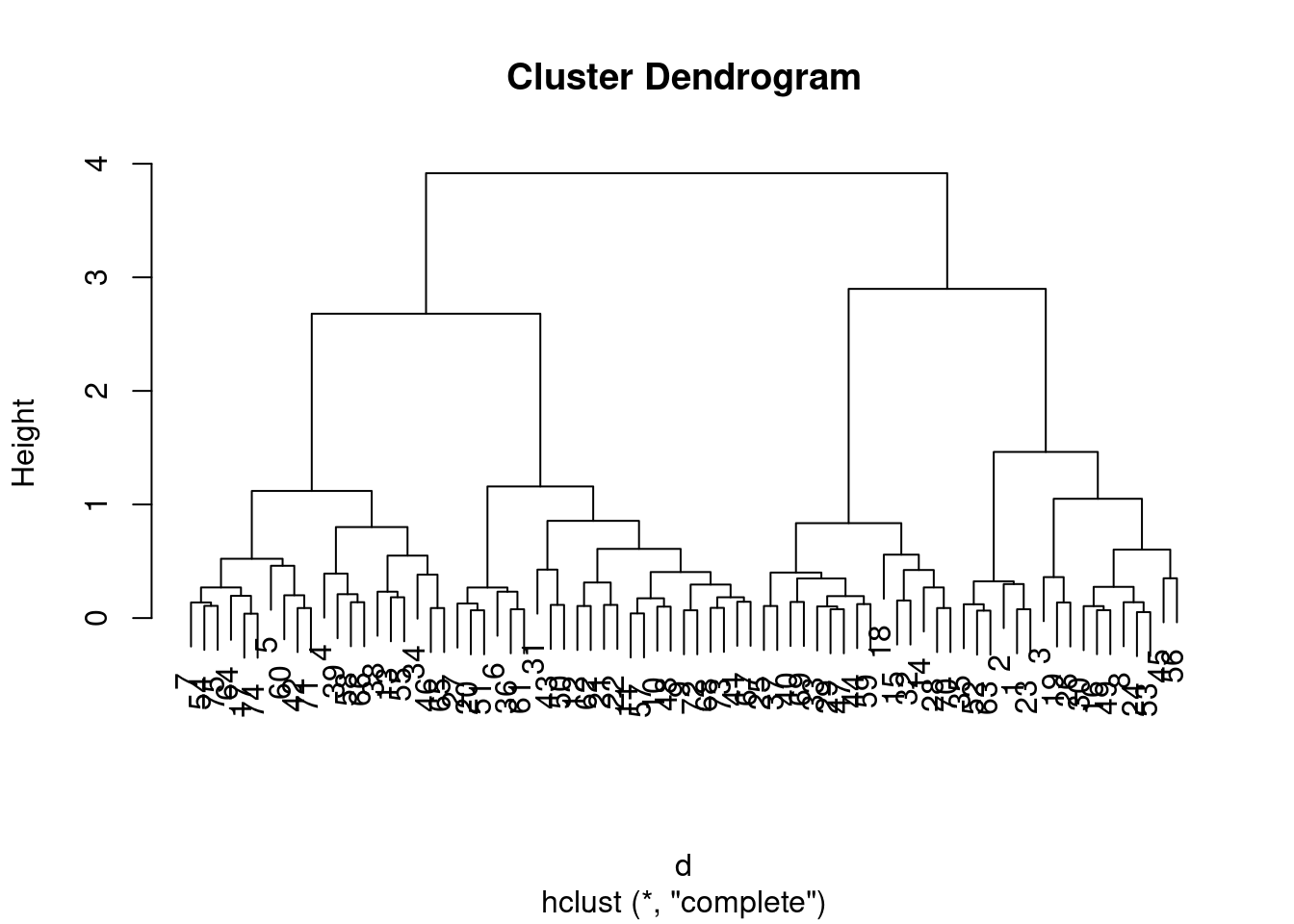

Use factoextra (ggplot version). We can specify the number of clusters to visualize how the dendrogram will be cut into clusters.

fviz_dend(hc, k = 4)

## Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as of ggplot2
## 3.3.4.
## ℹ The deprecated feature was likely used in the factoextra package.
##   Please report the issue at <https://github.com/kassambara/factoextra/issues>.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.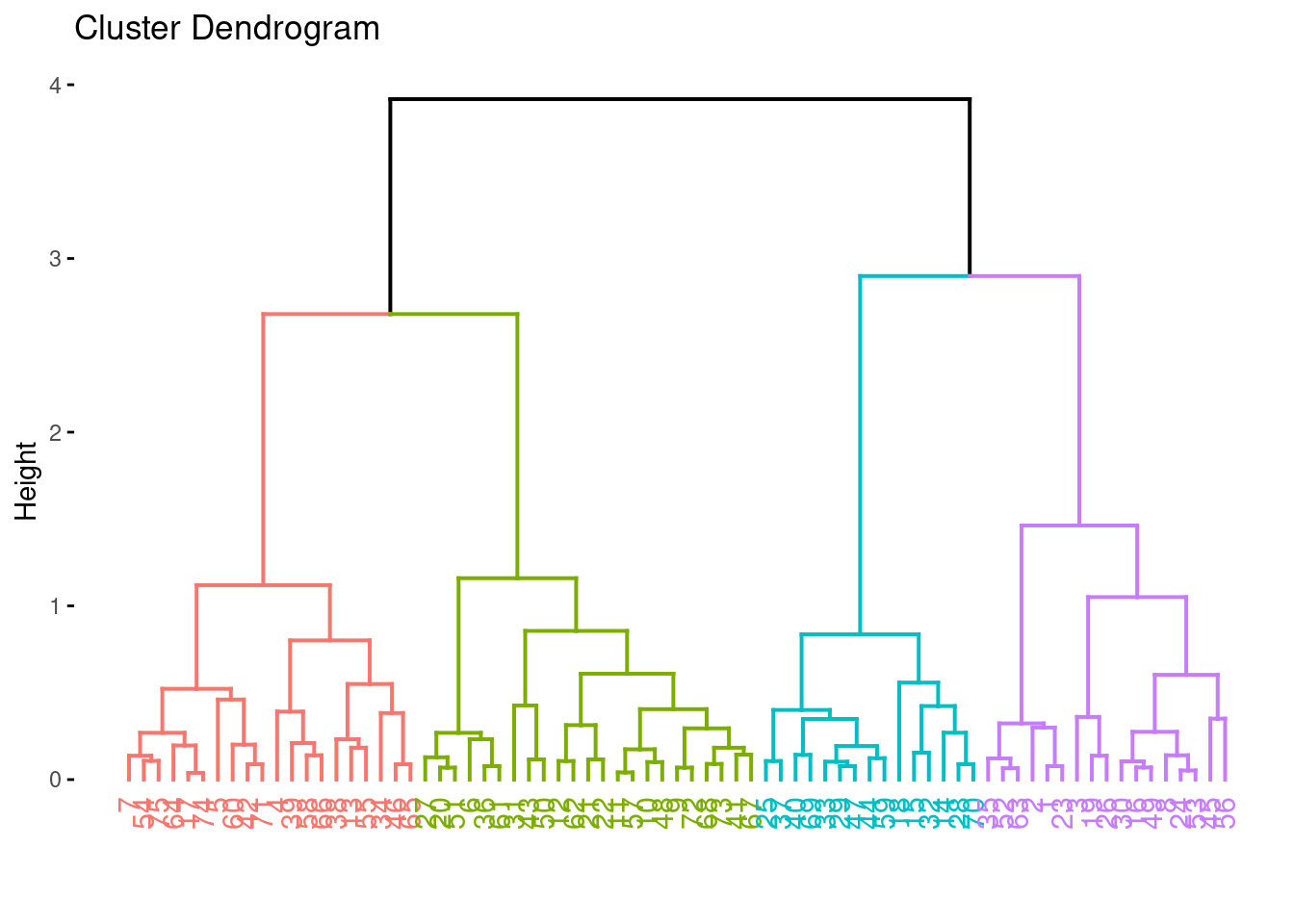

More plotting options for dendrograms, including plotting parts of large dendrograms can be found here.

Extract cluster assignments by cutting the dendrogram into four parts and add the cluster id to the data.

clusters <- cutree(hc, k = 4)
cluster_complete <- ruspini_scaled |>
  add_column(cluster = factor(clusters))
cluster_complete

## # A tibble: 75 × 3
##         x       y cluster
##     <dbl>   <dbl> <fct>  
##  1  1.97   0.513  1      
##  2  1.84   0.698  1      
##  3  0.987  0.0816 1      
##  4 -1.41  -0.0827 2      
##  5 -0.619 -0.411  2      
##  6 -0.881  1.13   3      
##  7 -1.01  -0.699  2      
##  8  1.45   0.739  1      
##  9 -0.291  1.03   3      
## 10 -0.553  1.21   3      
## # ℹ 65 more rows

ggplot(cluster_complete, aes(x, y, color = cluster)) +
  geom_point()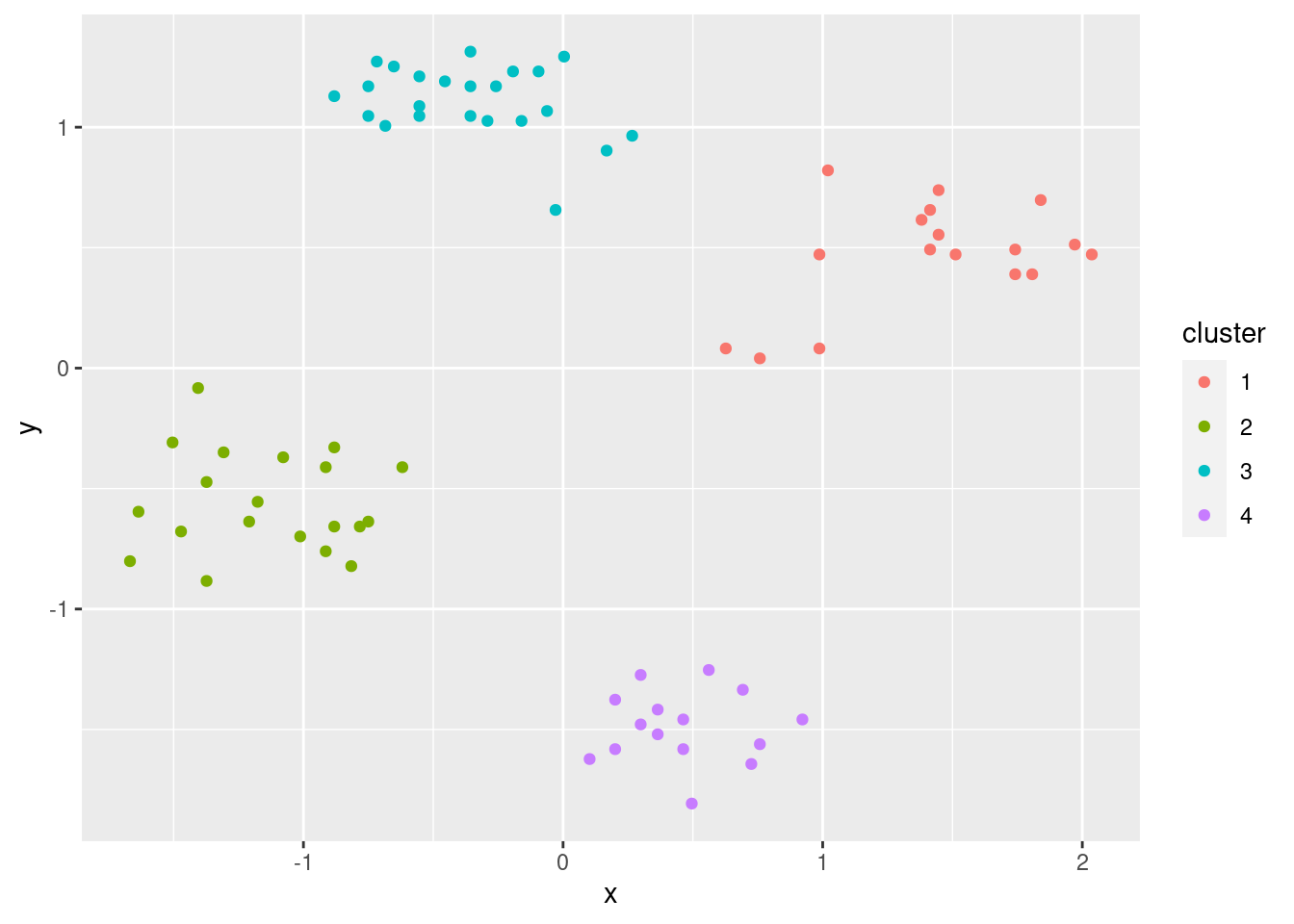

Try 8 clusters (Note: fviz_cluster needs a list with data and the cluster labels for hclust)

fviz_cluster(list(data = ruspini_scaled, cluster = cutree(hc, k = 8)), geom = "point")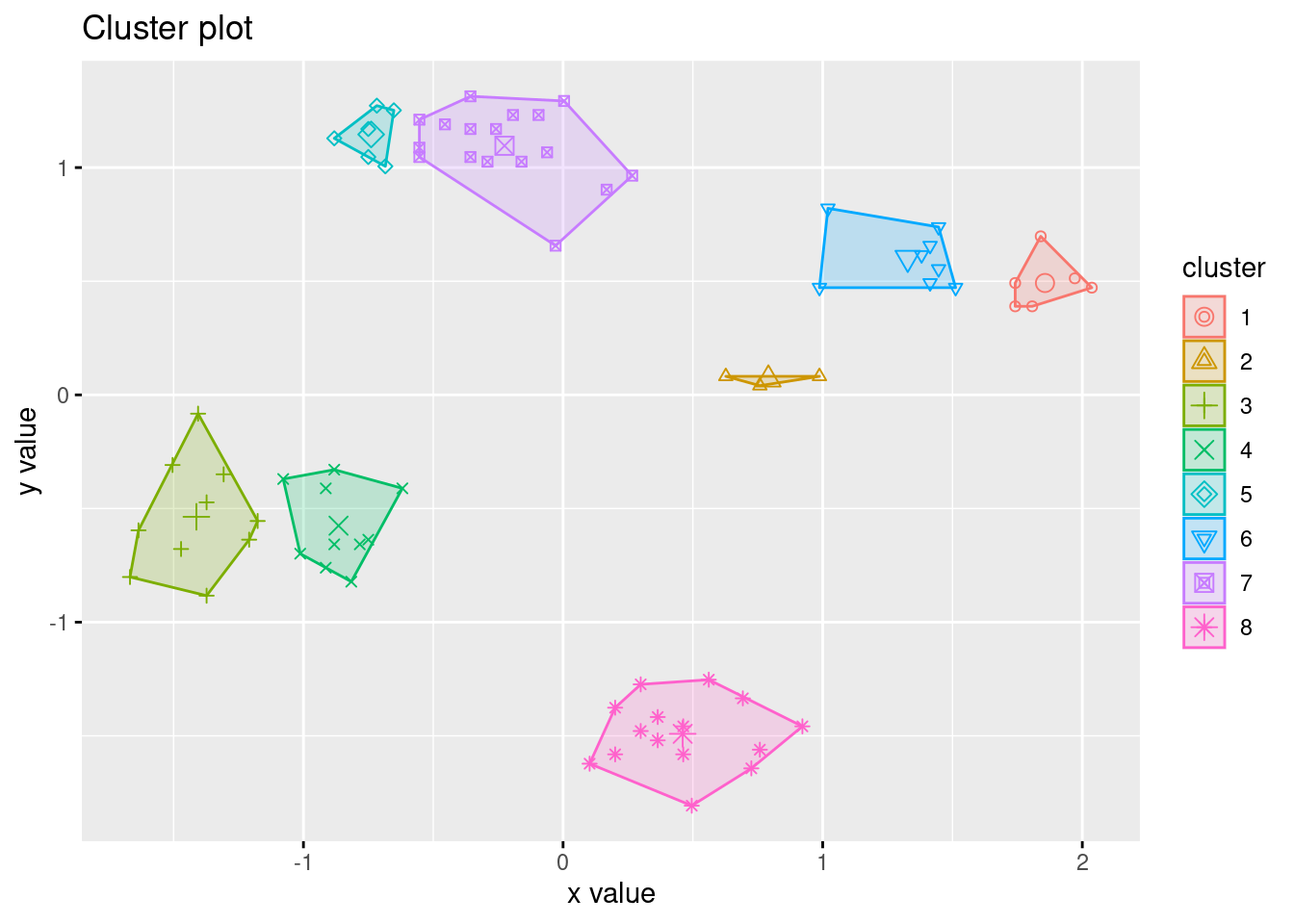

Clustering with single link

hc_single <- hclust(d, method = "single")
fviz_dend(hc_single, k = 4)

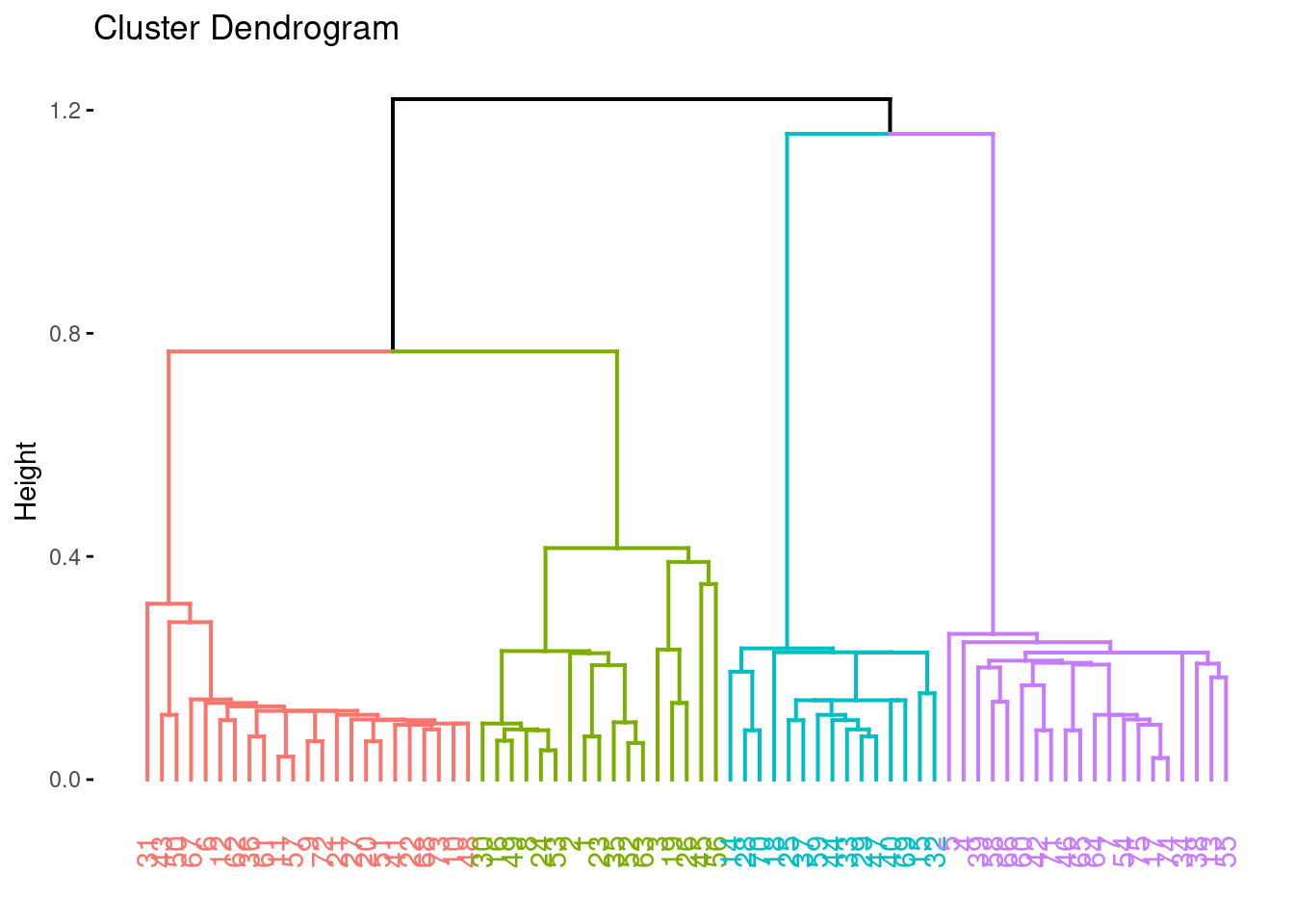
fviz_cluster(list(data = ruspini_scaled, cluster = cutree(hc_single, k = 4)), geom = "point")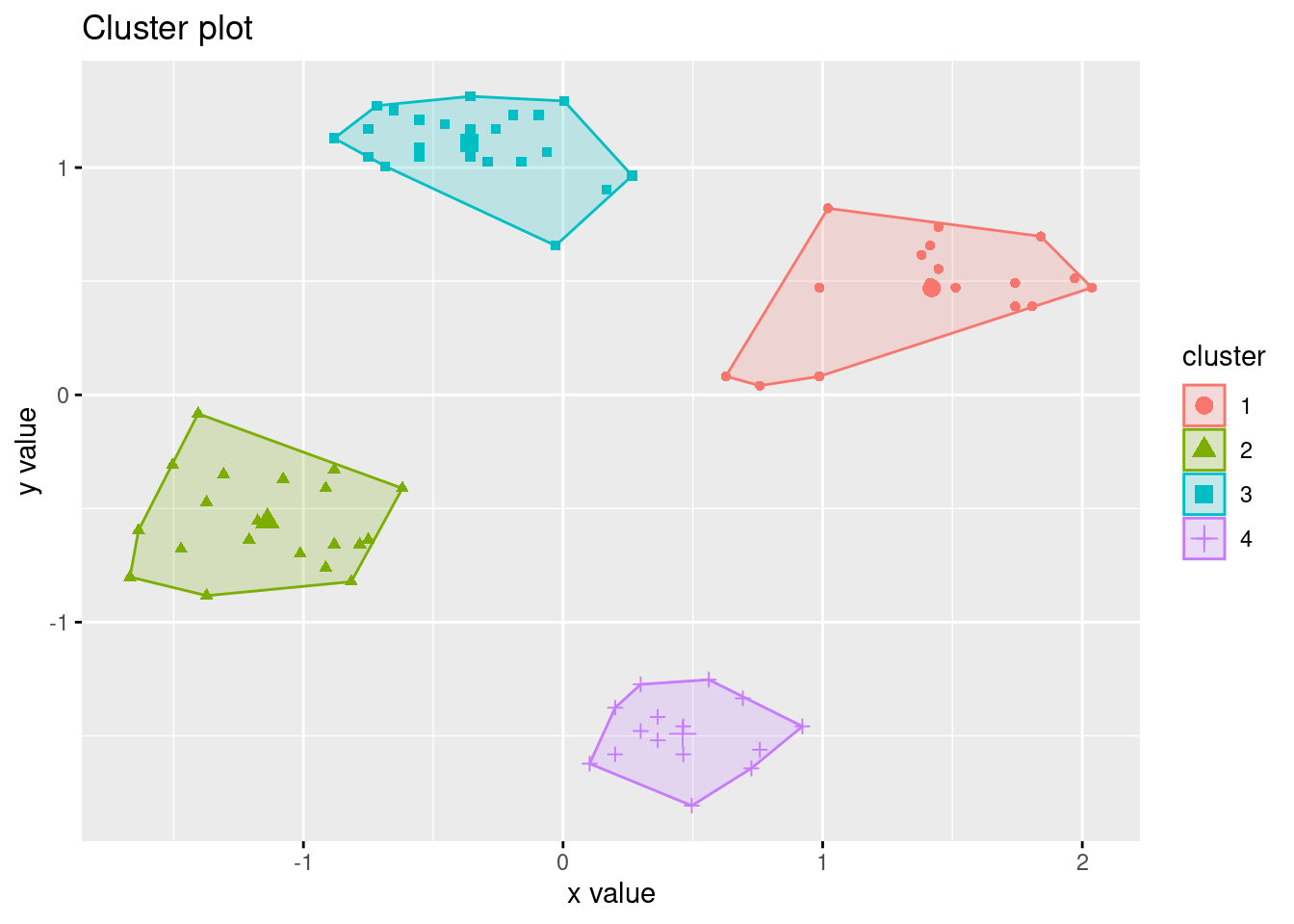

7.3.3 Density-based clustering with DBSCAN

library(dbscan)

## 
## Attaching package: 'dbscan'

## The following object is masked from 'package:stats':
## 
##     as.dendrogram

DBSCAN stands for “Density-Based Spatial Clustering of Applications with Noise.” It groups together points that are closely packed together and treats points in low-density regions as outliers.

Parameters: minPts defines how many points in the epsilon neighborhood are needed to make a point a core point. It is often chosen as a smoothing parameter. I use here minPts = 4.

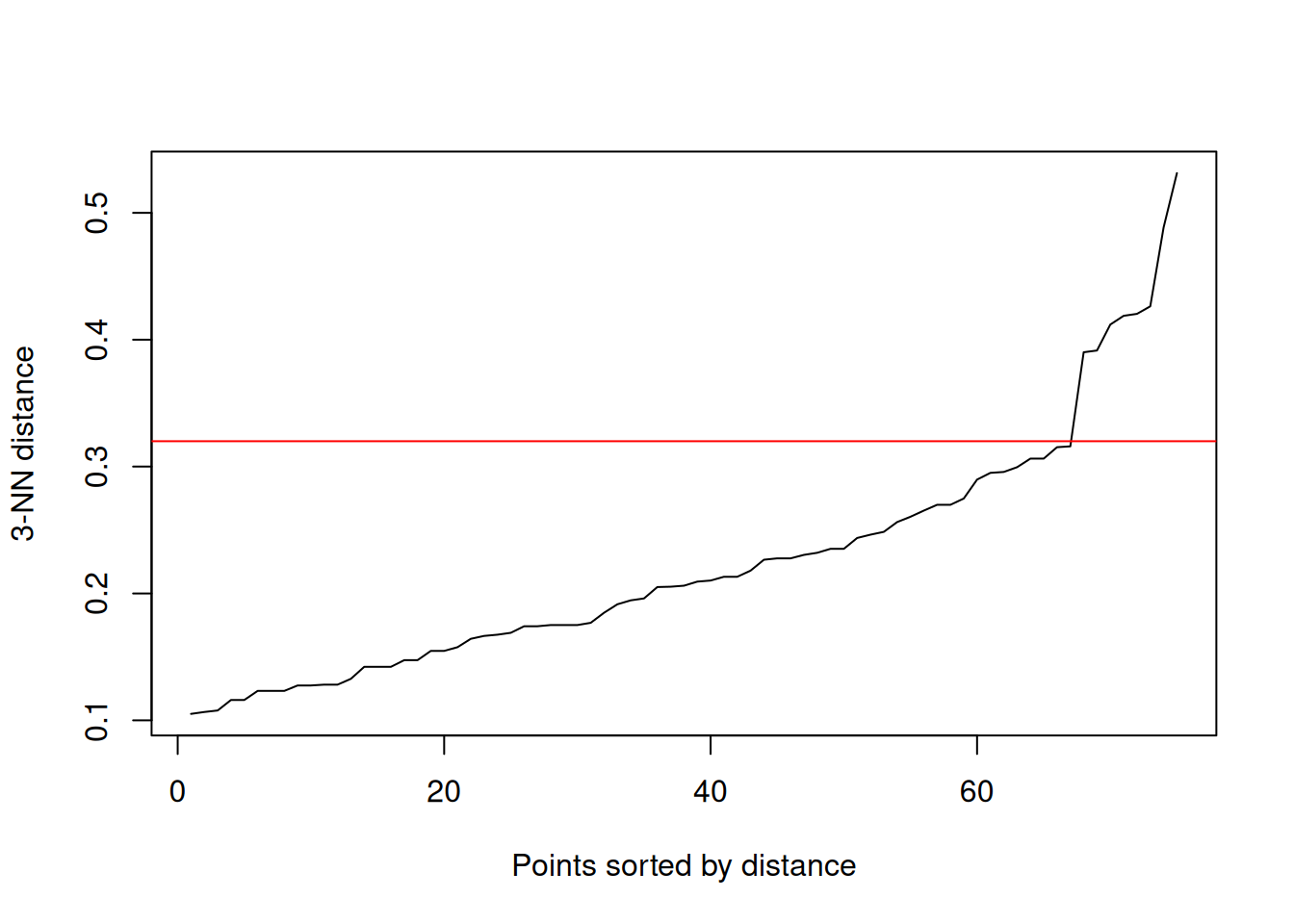
To decide on epsilon, the knee in the kNN distance plot is often used. Note that minPts contains the point itself, while the k-nearest neighbor does not. We therefore have to use k = minPts - 1! The knee is around eps = .32.

kNNdistplot(ruspini_scaled, k = 3)
abline(h = .32, col = "red")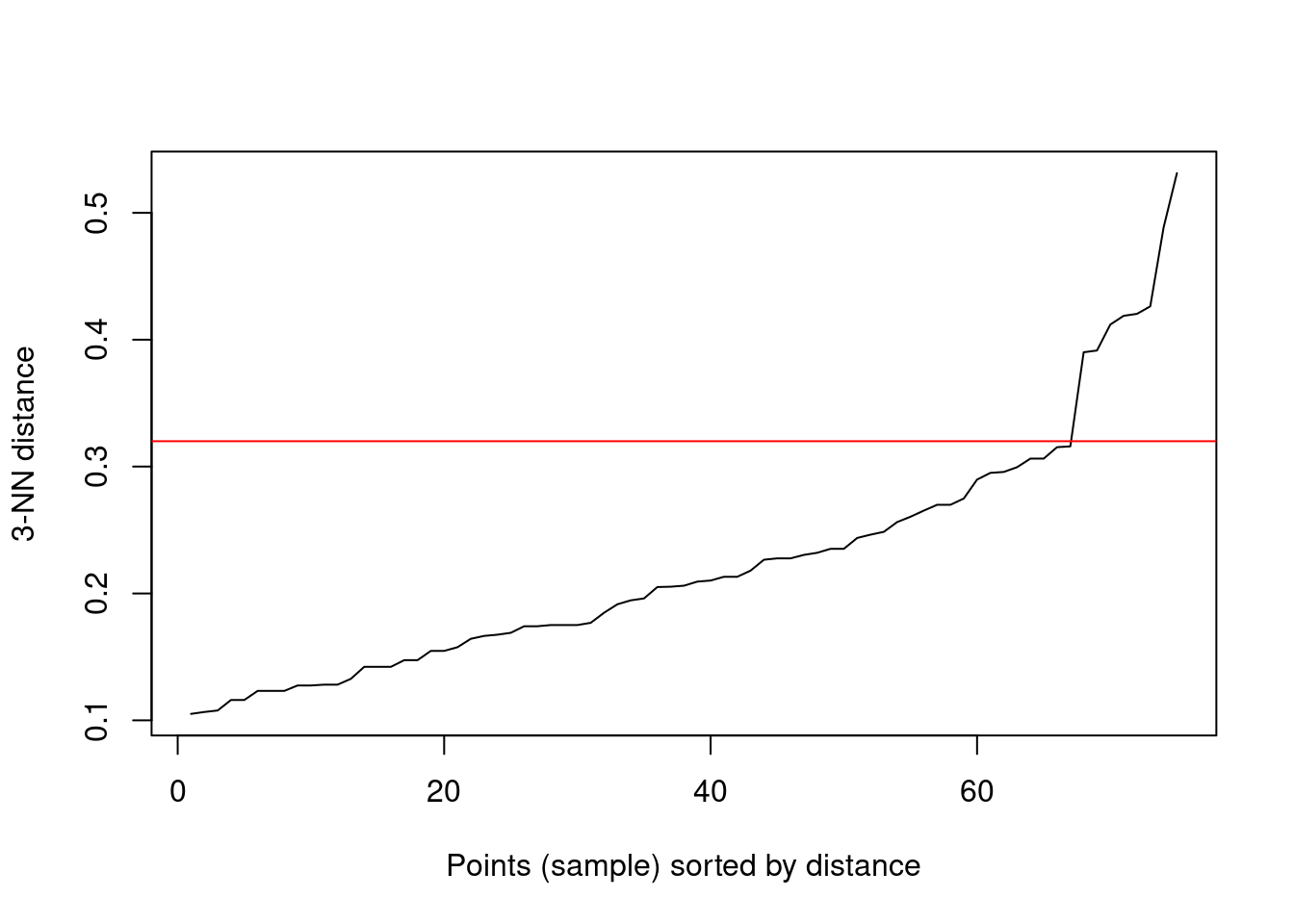

run dbscan

db <- dbscan(ruspini_scaled, eps = .32, minPts = 4)
db

## DBSCAN clustering for 75 objects.
## Parameters: eps = 0.32, minPts = 4
## Using euclidean distances and borderpoints = TRUE
## The clustering contains 4 cluster(s) and 5 noise points.
## 
##  0  1  2  3  4 
##  5 12 20 23 15 
## 
## Available fields: cluster, eps, minPts, dist,
##                   borderPoints

str(db)

## List of 5
##  $ cluster     : int [1:75] 1 1 0 2 2 3 2 1 3 3 ...
##  $ eps         : num 0.32
##  $ minPts      : num 4
##  $ dist        : chr "euclidean"
##  $ borderPoints: logi TRUE
##  - attr(*, "class")= chr [1:2] "dbscan_fast" "dbscan"

ggplot(ruspini_scaled |> add_column(cluster = factor(db$cluster)),
  aes(x, y, color = cluster)) + geom_point()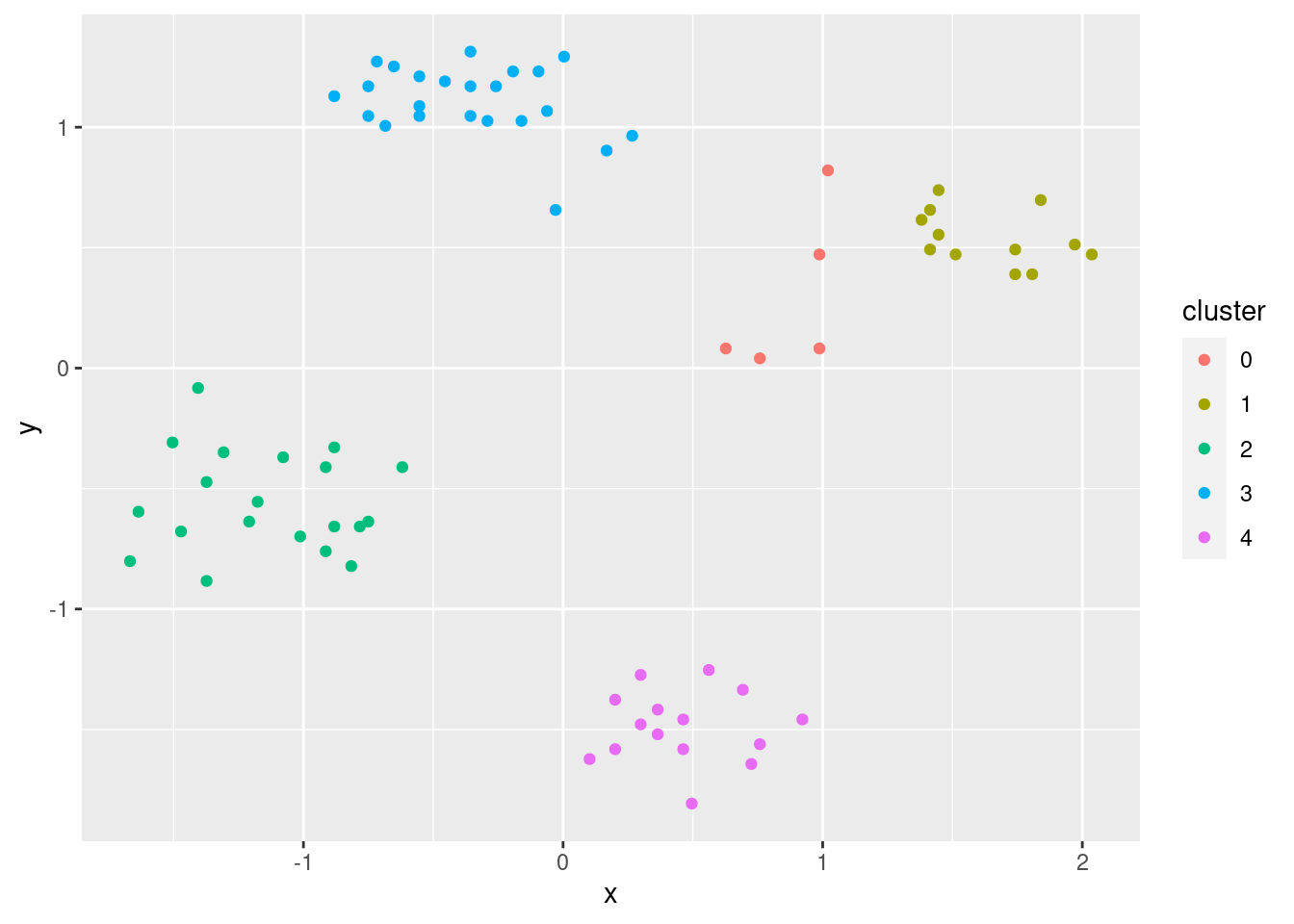

Note: Cluster 0 represents outliers).

fviz_cluster(db, ruspini_scaled, geom = "point")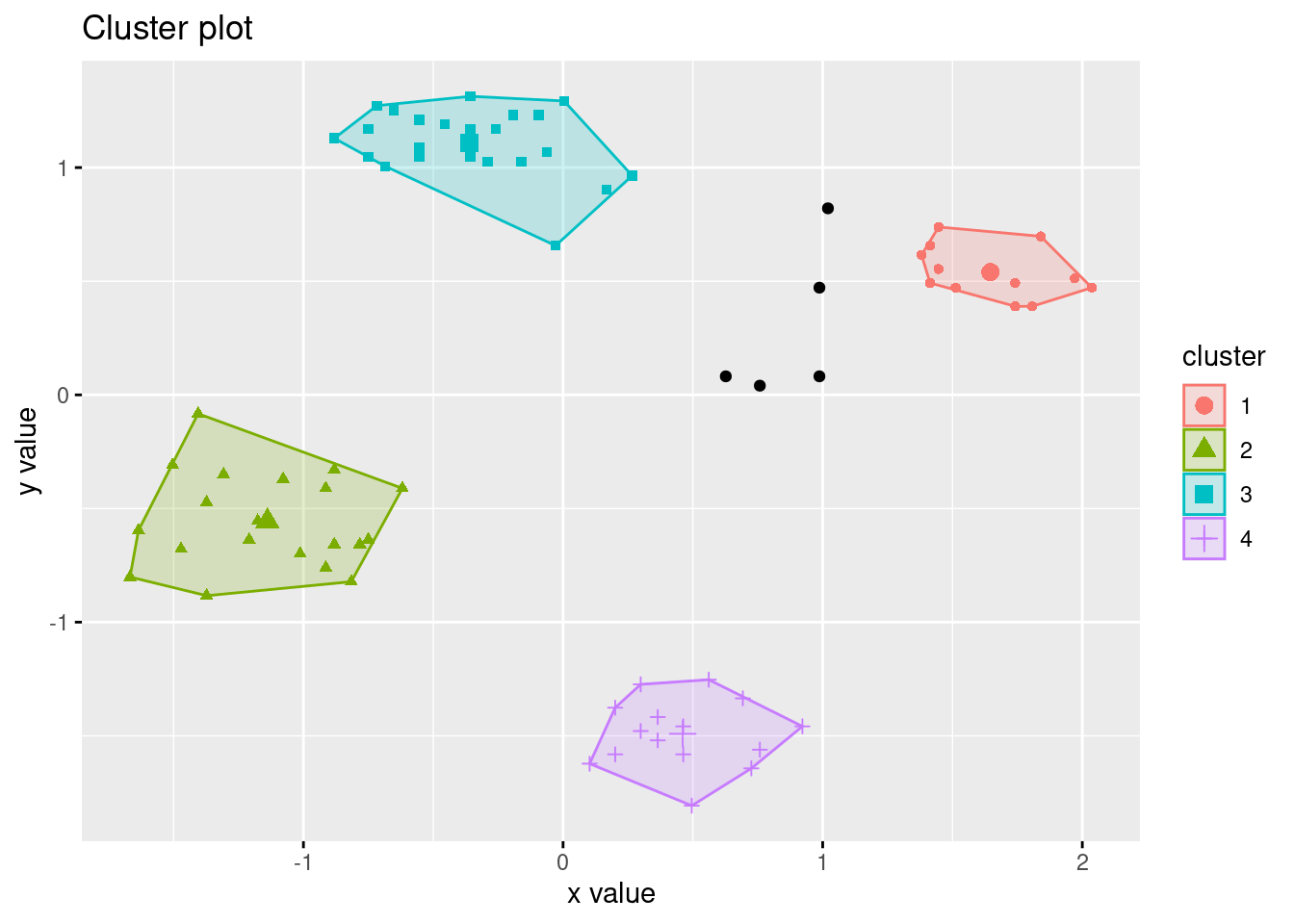

Play with eps (neighborhood size) and MinPts (minimum of points needed for core cluster)

7.3.4 Partitioning Around Medoids (PAM)

PAM tries to solve the $k$-medoids problem. The problem is similar to $k$-means, but uses medoids instead of centroids to represent clusters. Like hierarchical clustering, it typically works with precomputed distance matrix. An advantage is that you can use any distance metric not just Euclidean distances. Note: The medoid is the most central data point in the middle of the cluster.

library(cluster)

## 
## Attaching package: 'cluster'

## The following object is masked _by_ '.GlobalEnv':
## 
##     ruspini

d <- dist(ruspini_scaled)
str(d)

##  'dist' num [1:2775] 0.227 1.074 3.429 2.75 2.918 ...
##  - attr(*, "Size")= int 75
##  - attr(*, "Diag")= logi FALSE
##  - attr(*, "Upper")= logi FALSE
##  - attr(*, "method")= chr "Euclidean"
##  - attr(*, "call")= language dist(x = ruspini_scaled)

p <- pam(d, k = 4)
p

## Medoids:
##      ID   
## [1,] 49 49
## [2,] 46 46
## [3,] 41 41
## [4,] 44 44
## Clustering vector:
##  [1] 1 1 1 2 2 3 2 1 3 3 3 3 2 4 4 1 2 4 1 3 3 3 1 1 4
## [26] 1 3 4 4 1 3 4 4 2 1 3 4 2 2 4 3 2 3 4 1 2 4 3 1 3
## [51] 3 1 1 2 2 1 3 2 4 2 3 3 1 2 2 2 3 3 4 4 2 3 3 2 2
## Objective function:
## build  swap 
## 0.442 0.319 
## 
## Available components:
## [1] "medoids"    "id.med"     "clustering" "objective" 
## [5] "isolation"  "clusinfo"   "silinfo"    "diss"      
## [9] "call"

ruspini_clustered <- ruspini_scaled |> 
  add_column(cluster = factor(p$cluster))

medoids <- as_tibble(ruspini_scaled[p$medoids, ], rownames = "cluster")
medoids

## # A tibble: 4 × 3
##   cluster      x      y
##   <chr>    <dbl>  <dbl>
## 1 1        1.45   0.554
## 2 2       -1.18  -0.555
## 3 3       -0.357  1.17 
## 4 4        0.463 -1.46

ggplot(ruspini_clustered, aes(x = x, y = y, color = cluster)) + 
  geom_point() +
  geom_point(data = medoids, aes(x = x, y = y, color = cluster), shape = 3, size = 10)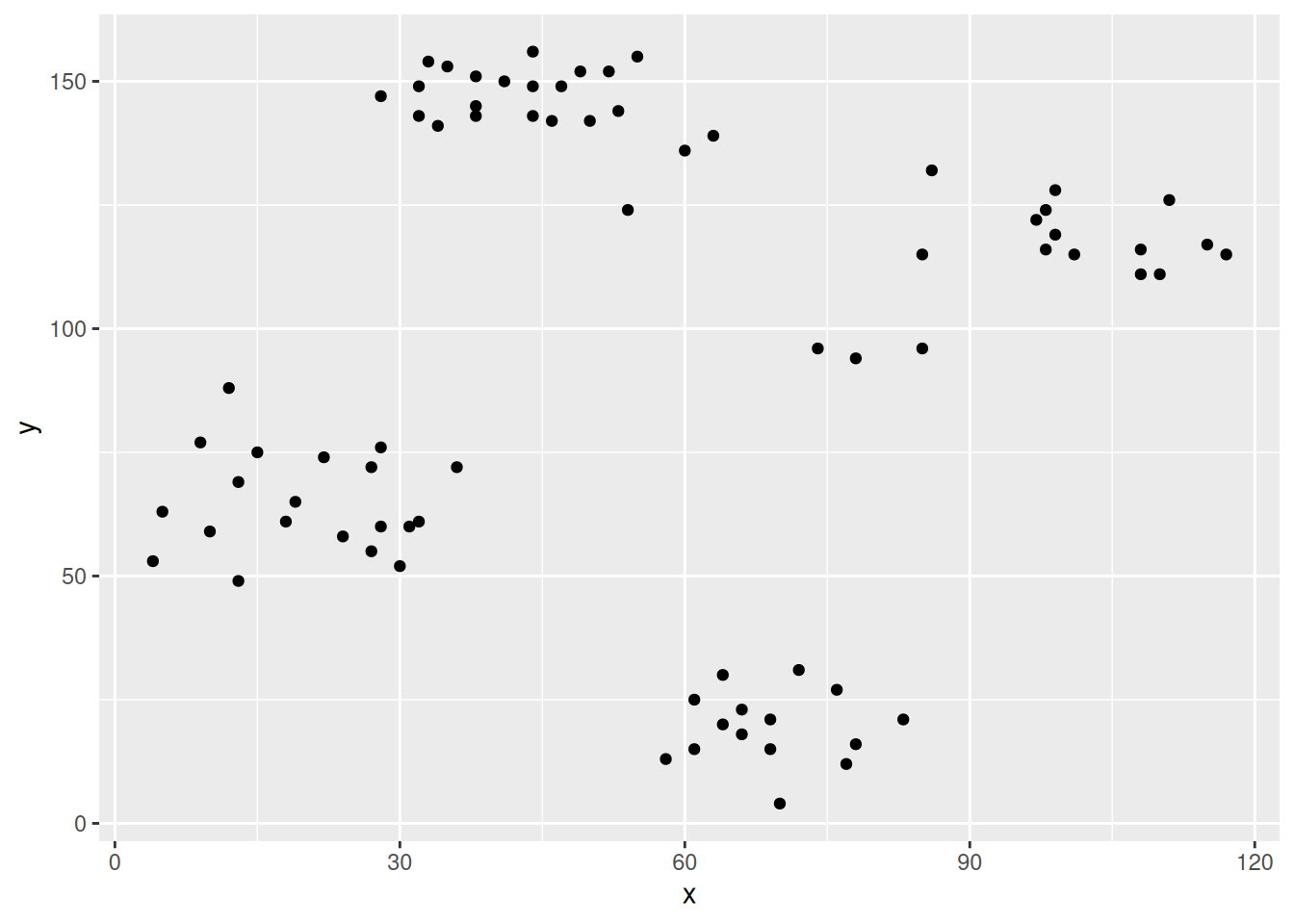

## __Note:__ `fviz_cluster` needs the original data.
fviz_cluster(c(p, list(data = ruspini_scaled)), geom = "point", ellipse.type = "norm")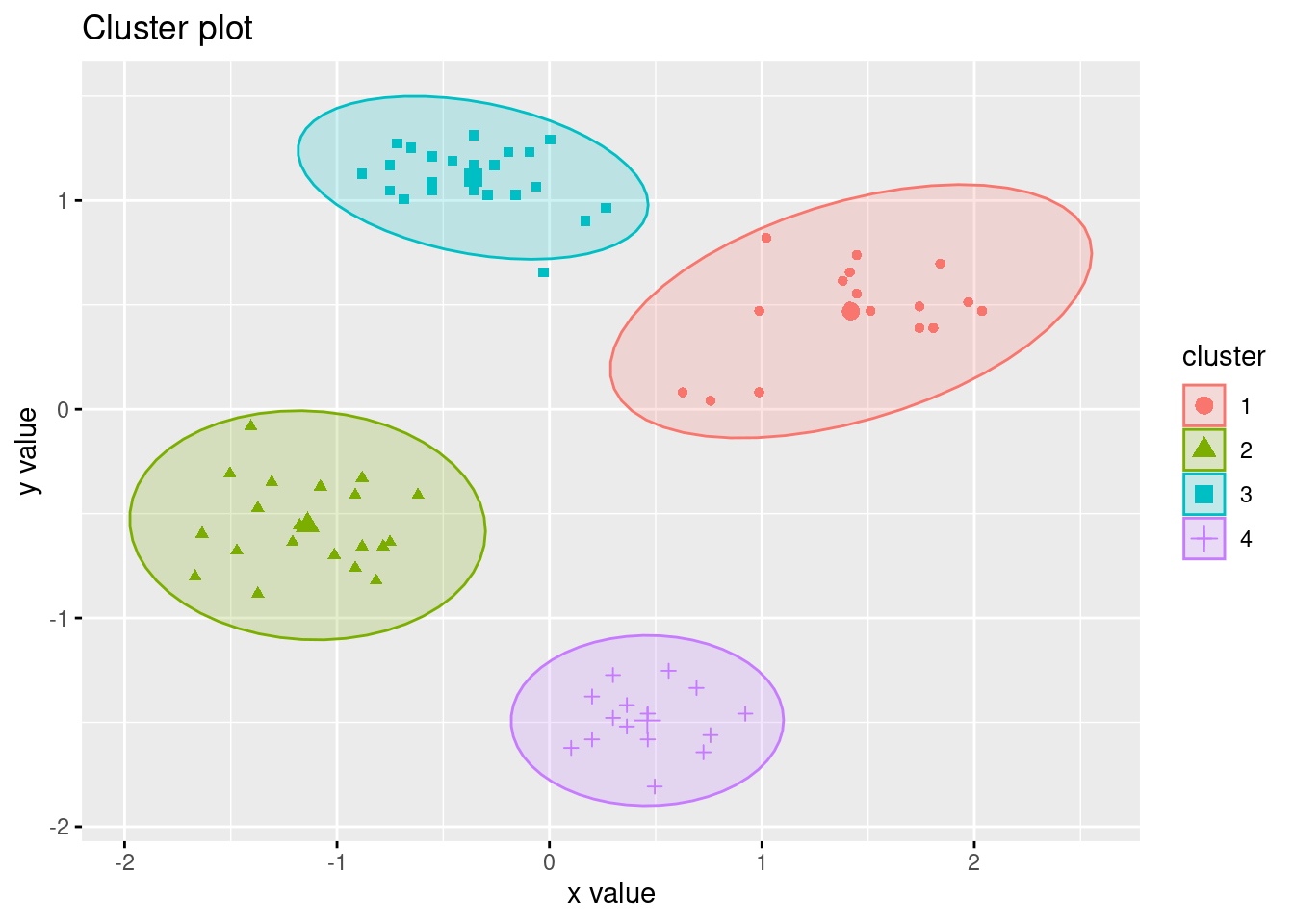

7.3.5 Gaussian Mixture Models

library(mclust)

## Package 'mclust' version 6.0.0
## Type 'citation("mclust")' for citing this R package in publications.

## 
## Attaching package: 'mclust'

## The following object is masked from 'package:purrr':
## 
##     map

Gaussian mixture models assume that the data set is the result of drawing data from a set of Gaussian distributions where each distribution represents a cluster. Estimation algorithms try to identify the location parameters of the distributions and thus can be used to find clusters. Mclust() uses Bayesian Information Criterion (BIC) to find the number of clusters (model selection). BIC uses the likelihood and a penalty term to guard against overfitting.

m <- Mclust(ruspini_scaled)
summary(m)

## ---------------------------------------------------- 
## Gaussian finite mixture model fitted by EM algorithm 
## ---------------------------------------------------- 
## 
## Mclust EEI (diagonal, equal volume and shape) model
## with 5 components: 
## 
##  log-likelihood  n df  BIC  ICL
##           -91.3 75 16 -252 -252
## 
## Clustering table:
##  1  2  3  4  5 
## 14  3 20 23 15

plot(m, what = "classification")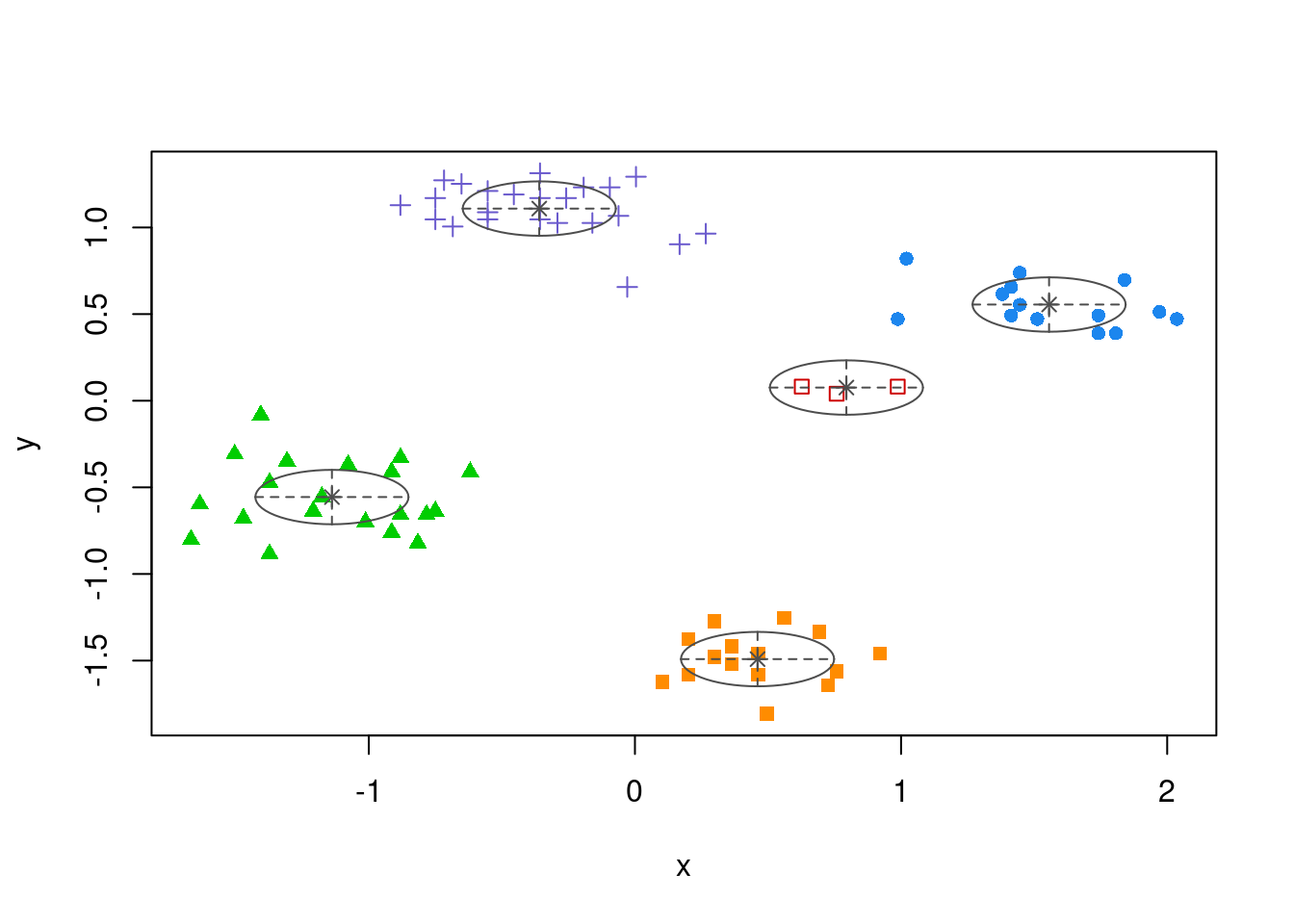

Rerun with a fixed number of 4 clusters

m <- Mclust(ruspini_scaled, G=4)
summary(m)

## ---------------------------------------------------- 
## Gaussian finite mixture model fitted by EM algorithm 
## ---------------------------------------------------- 
## 
## Mclust EEI (diagonal, equal volume and shape) model
## with 4 components: 
## 
##  log-likelihood  n df  BIC  ICL
##            -102 75 13 -259 -259
## 
## Clustering table:
##  1  2  3  4 
## 17 20 23 15

plot(m, what = "classification")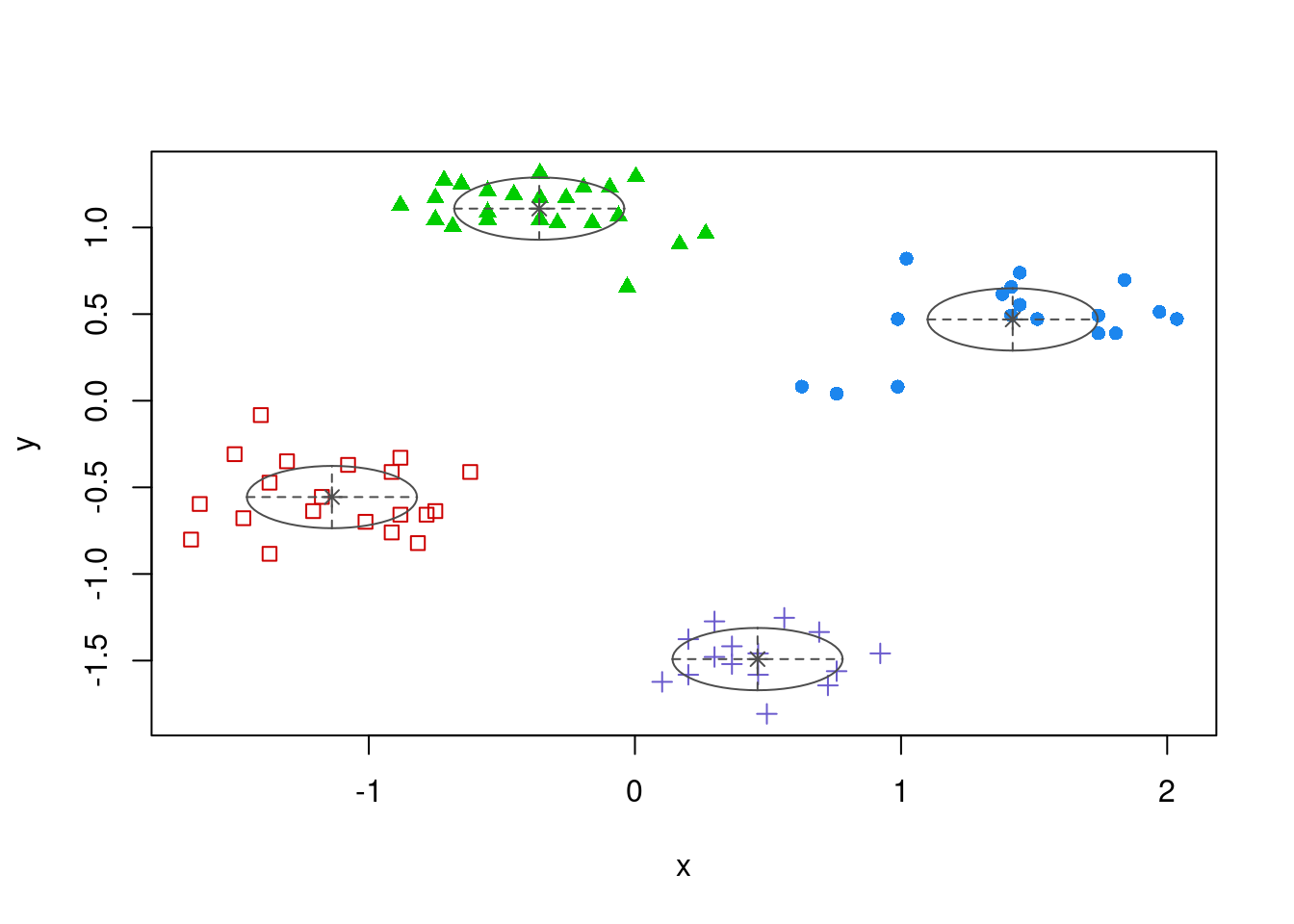

7.3.6 Spectral clustering

Spectral clustering works by embedding the data points of the partitioning problem into the subspace of the k largest eigenvectors of a normalized affinity/kernel matrix. Then uses a simple clustering method like k-means.

library("kernlab")

## 
## Attaching package: 'kernlab'

## The following object is masked from 'package:scales':
## 
##     alpha

## The following object is masked from 'package:arules':
## 
##     size

## The following object is masked from 'package:purrr':
## 
##     cross

## The following object is masked from 'package:ggplot2':
## 
##     alpha

cluster_spec <- specc(as.matrix(ruspini_scaled), centers = 4)
cluster_spec

## Spectral Clustering object of class "specc" 
## 
##  Cluster memberships: 
##  
## 1 1 1 1 1 2 1 1 2 2 2 2 1 3 4 1 1 4 1 2 2 2 1 1 4 1 2 3 4 1 2 3 4 1 1 2 4 1 1 4 2 1 2 4 1 1 4 2 1 2 2 1 1 1 1 1 2 1 4 1 2 2 1 1 1 1 2 2 4 3 1 2 2 1 1 
##  
## Gaussian Radial Basis kernel function. 
##  Hyperparameter : sigma =  41.7670067458421 
## 
## Centers:  
##         [,1]    [,2]
## [1,]  0.0367 -0.0849
## [2,] -0.3595  1.1091
## [3,]  0.7416 -1.4789
## [4,]  0.3586 -1.4957
## 
## Cluster size:  
## [1] 37 23  4 11
## 
## Within-cluster sum of squares:  
## [1] 75.6 52.0 18.8 37.1

ggplot(ruspini_scaled |> 
         add_column(cluster = factor(cluster_spec)),
  aes(x, y, color = cluster)) + 
  geom_point()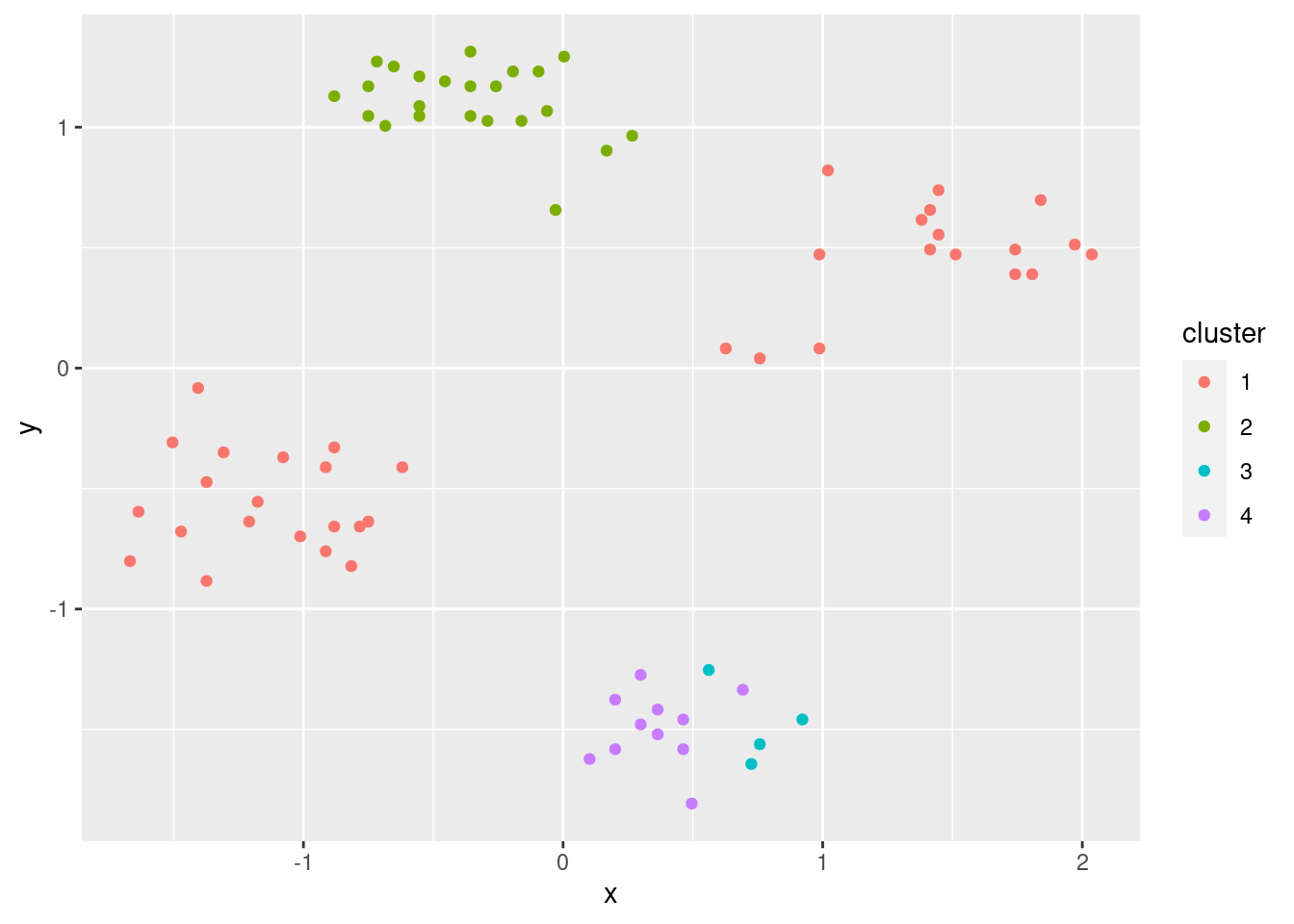

7.3.7 Fuzzy C-Means Clustering

The fuzzy clustering version of the k-means clustering problem. Each data point has a degree of membership to for each cluster.

library("e1071")

cluster_cmeans <- cmeans(as.matrix(ruspini_scaled), centers = 4)
cluster_cmeans

## Fuzzy c-means clustering with 4 clusters
## 
## Cluster centers:
##        x      y
## 1 -0.376  1.114
## 2  0.455 -1.476
## 3 -1.137 -0.555
## 4  1.505  0.516
## 
## Memberships:
##              1        2        3        4
##  [1,] 3.39e-02 0.031838 0.018432 9.16e-01
##  [2,] 2.68e-02 0.020544 0.013080 9.40e-01
##  [3,] 1.10e-01 0.118859 0.065467 7.06e-01
##  [4,] 9.82e-02 0.045277 0.828834 2.77e-02
##  [5,] 9.31e-02 0.097120 0.768391 4.14e-02
##  [6,] 8.62e-01 0.025668 0.075850 3.63e-02
##  [7,] 9.54e-03 0.012774 0.973170 4.51e-03
##  [8,] 1.48e-02 0.008725 0.006153 9.70e-01
##  [9,] 9.89e-01 0.002182 0.004627 4.27e-03
## [10,] 9.75e-01 0.004817 0.011470 8.41e-03
## [11,] 9.79e-01 0.004135 0.010326 6.88e-03
## [12,] 9.60e-01 0.007890 0.015164 1.73e-02
## [13,] 2.69e-02 0.027262 0.934341 1.15e-02
## [14,] 2.34e-02 0.892180 0.038484 4.59e-02
## [15,] 1.02e-02 0.953744 0.018343 1.78e-02
## [16,] 2.46e-03 0.001840 0.001160 9.95e-01
## [17,] 3.66e-02 0.054960 0.890097 1.83e-02
## [18,] 1.14e-02 0.947252 0.024935 1.65e-02
## [19,] 1.74e-01 0.177389 0.107509 5.41e-01
## [20,] 9.25e-01 0.014629 0.037153 2.37e-02
## [21,] 8.92e-01 0.019994 0.033363 5.51e-02
## [22,] 9.40e-01 0.011470 0.020462 2.85e-02
## [23,] 4.09e-02 0.040522 0.022924 8.96e-01
## [24,] 7.44e-03 0.004748 0.003221 9.85e-01
## [25,] 9.53e-03 0.953143 0.025463 1.19e-02
## [26,] 2.18e-01 0.183757 0.128308 4.70e-01
## [27,] 9.19e-01 0.015519 0.041982 2.38e-02
## [28,] 1.09e-02 0.950362 0.020593 1.82e-02
## [29,] 1.35e-03 0.993633 0.003167 1.85e-03
## [30,] 5.07e-04 0.000411 0.000250 9.99e-01
## [31,] 7.51e-01 0.051906 0.092068 1.05e-01
## [32,] 9.02e-03 0.959100 0.017339 1.45e-02
## [33,] 1.66e-03 0.992177 0.003861 2.30e-03
## [34,] 3.00e-02 0.040506 0.914867 1.46e-02
## [35,] 1.13e-02 0.009962 0.005870 9.73e-01
## [36,] 9.10e-01 0.016805 0.048384 2.45e-02
## [37,] 1.73e-02 0.912542 0.049812 2.04e-02
## [38,] 5.52e-02 0.059385 0.860423 2.50e-02
## [39,] 5.31e-02 0.033635 0.895310 1.80e-02
## [40,] 1.08e-02 0.947018 0.028739 1.34e-02
## [41,] 9.98e-01 0.000451 0.000964 8.88e-04
## [42,] 2.54e-02 0.022071 0.942653 9.90e-03
## [43,] 7.55e-01 0.044822 0.067224 1.33e-01
## [44,] 5.05e-05 0.999766 0.000110 7.42e-05
## [45,] 9.62e-02 0.053620 0.039261 8.11e-01
## [46,] 4.47e-04 0.000437 0.998932 1.84e-04
## [47,] 3.35e-03 0.983990 0.008241 4.42e-03
## [48,] 9.92e-01 0.001497 0.003385 2.77e-03
## [49,] 1.32e-03 0.000943 0.000609 9.97e-01
## [50,] 7.02e-01 0.050971 0.071389 1.76e-01
## [51,] 9.47e-01 0.010355 0.025638 1.73e-02
## [52,] 1.39e-02 0.013539 0.007574 9.65e-01
## [53,] 8.07e-03 0.005042 0.003456 9.83e-01
## [54,] 2.25e-02 0.035817 0.930269 1.14e-02
## [55,] 4.92e-02 0.043110 0.887727 2.00e-02
## [56,] 1.27e-01 0.046128 0.039417 7.88e-01
## [57,] 9.75e-01 0.004750 0.012064 7.76e-03
## [58,] 2.26e-02 0.015521 0.954072 7.84e-03
## [59,] 1.40e-03 0.993497 0.003079 2.03e-03
## [60,] 1.36e-02 0.010238 0.971283 4.91e-03
## [61,] 9.29e-01 0.013313 0.037605 1.97e-02
## [62,] 9.27e-01 0.013940 0.024785 3.40e-02
## [63,] 1.93e-02 0.019236 0.010680 9.51e-01
## [64,] 3.84e-02 0.074030 0.866516 2.11e-02
## [65,] 3.14e-03 0.003403 0.992094 1.36e-03
## [66,] 1.71e-02 0.013810 0.962604 6.49e-03
## [67,] 9.76e-01 0.004635 0.009541 9.54e-03
## [68,] 9.89e-01 0.002238 0.004484 4.75e-03
## [69,] 1.01e-02 0.952362 0.024151 1.34e-02
## [70,] 1.11e-02 0.949234 0.020387 1.93e-02
## [71,] 4.51e-02 0.033977 0.904508 1.64e-02
## [72,] 9.96e-01 0.000705 0.001560 1.32e-03
## [73,] 9.69e-01 0.005928 0.011252 1.35e-02
## [74,] 4.26e-02 0.063341 0.872767 2.13e-02
## [75,] 2.10e-02 0.029083 0.939773 1.01e-02
## 
## Closest hard clustering:
##  [1] 4 4 4 3 3 1 3 4 1 1 1 1 3 2 2 4 3 2 4 1 1 1 4 4 2
## [26] 4 1 2 2 4 1 2 2 3 4 1 2 3 3 2 1 3 1 2 4 3 2 1 4 1
## [51] 1 4 4 3 3 4 1 3 2 3 1 1 4 3 3 3 1 1 2 2 3 1 1 3 3
## 
## Available components:
## [1] "centers"     "size"        "cluster"    
## [4] "membership"  "iter"        "withinerror"
## [7] "call"

Plot membership (shown as small pie charts)

library("scatterpie")
ggplot()  +
  geom_scatterpie(data = cbind(ruspini_scaled, cluster_cmeans$membership),
    aes(x = x, y = y), cols = colnames(cluster_cmeans$membership), legend_name = "Membership") + coord_equal()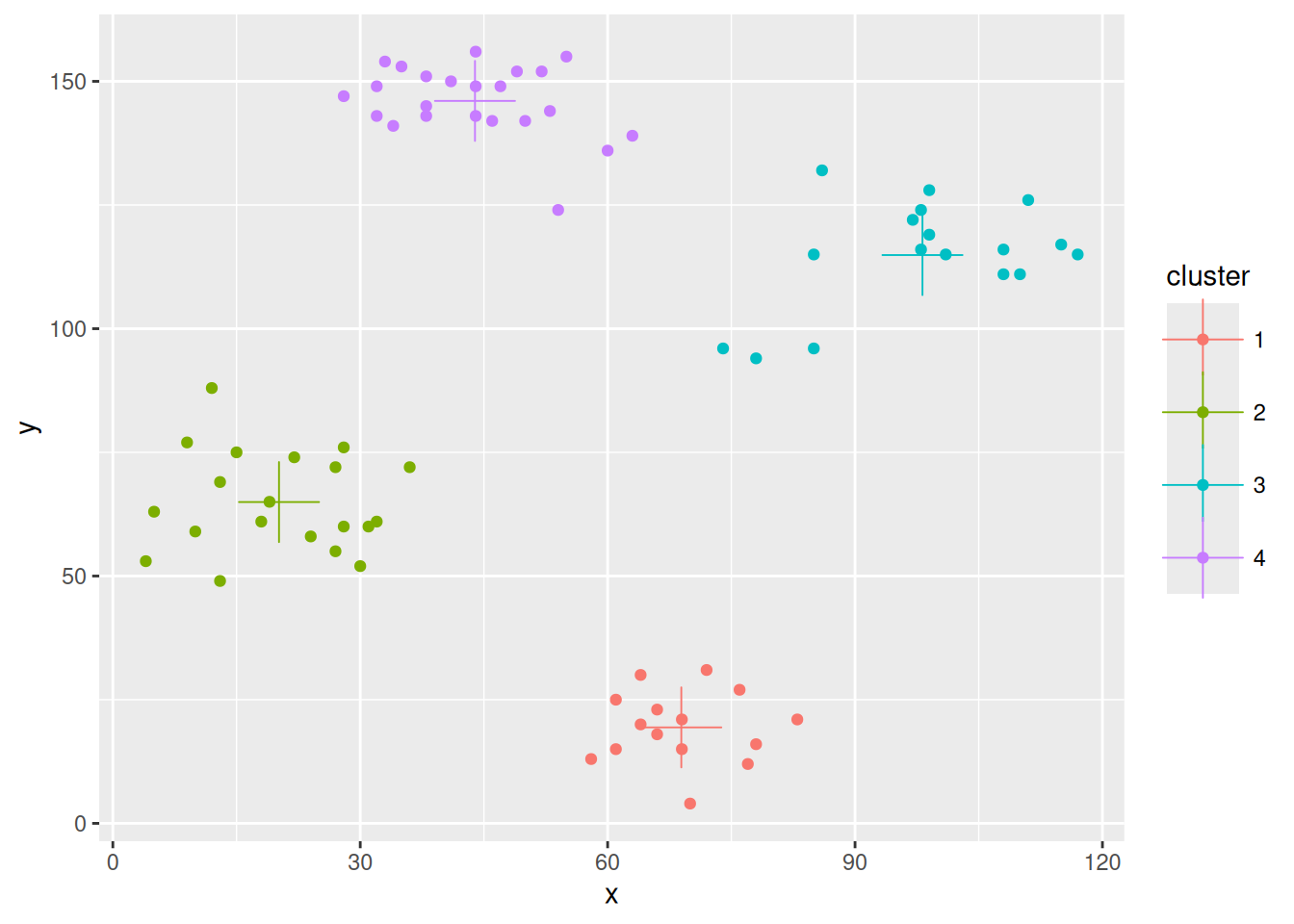

7.4 Internal Cluster Validation

7.4.1 Compare the Clustering Quality

The two most popular quality metrics are the within-cluster sum of squares (WCSS) used by $k$-means and the average silhouette width. Look at within.cluster.ss and avg.silwidth below.

##library(fpc)

Notes: * I do not load fpc since the NAMESPACE overwrites dbscan. * The clustering (second argument below) has to be supplied as a vector with numbers (cluster IDs) and cannot be a factor (use as.integer() to convert the factor to an ID).

fpc::cluster.stats(d, km$cluster)

## $n
## [1] 75
## 
## $cluster.number
## [1] 4
## 
## $cluster.size
## [1] 23 17 15 20
## 
## $min.cluster.size
## [1] 15
## 
## $noisen
## [1] 0
## 
## $diameter
## [1] 1.159 1.463 0.836 1.119
## 
## $average.distance
## [1] 0.429 0.581 0.356 0.482
## 
## $median.distance
## [1] 0.393 0.502 0.338 0.449
## 
## $separation
## [1] 0.768 0.768 1.158 1.158
## 
## $average.toother
## [1] 2.15 2.29 2.31 2.16
## 
## $separation.matrix
##       [,1]  [,2] [,3] [,4]
## [1,] 0.000 0.768 1.96 1.22
## [2,] 0.768 0.000 1.31 1.34
## [3,] 1.958 1.308 0.00 1.16
## [4,] 1.220 1.340 1.16 0.00
## 
## $ave.between.matrix
##      [,1] [,2] [,3] [,4]
## [1,] 0.00 1.92 2.75 1.89
## [2,] 1.92 0.00 2.22 2.77
## [3,] 2.75 2.22 0.00 1.87
## [4,] 1.89 2.77 1.87 0.00
## 
## $average.between
## [1] 2.22
## 
## $average.within
## [1] 0.463
## 
## $n.between
## [1] 2091
## 
## $n.within
## [1] 684
## 
## $max.diameter
## [1] 1.46
## 
## $min.separation
## [1] 0.768
## 
## $within.cluster.ss
## [1] 10.1
## 
## $clus.avg.silwidths
##     1     2     3     4 
## 0.745 0.681 0.807 0.721 
## 
## $avg.silwidth
## [1] 0.737
## 
## $g2
## NULL
## 
## $g3
## NULL
## 
## $pearsongamma
## [1] 0.842
## 
## $dunn
## [1] 0.525
## 
## $dunn2
## [1] 3.23
## 
## $entropy
## [1] 1.37
## 
## $wb.ratio
## [1] 0.209
## 
## $ch
## [1] 324
## 
## $cwidegap
## [1] 0.315 0.415 0.235 0.261
## 
## $widestgap
## [1] 0.415
## 
## $sindex
## [1] 0.858
## 
## $corrected.rand
## NULL
## 
## $vi
## NULL

Read ? cluster.stats for an explanation of all the available indices.

sapply(
  list(
    km = km$cluster,
    hc_compl = cutree(hc, k = 4),
    hc_single = cutree(hc_single, k = 4)
  ),
  FUN = function(x)
    fpc::cluster.stats(d, x))[c("within.cluster.ss", "avg.silwidth"), ]

##                   km    hc_compl hc_single
## within.cluster.ss 10.1  10.1     10.1     
## avg.silwidth      0.737 0.737    0.737

7.4.2 Silhouette plot

library(cluster)
plot(silhouette(km$cluster, d))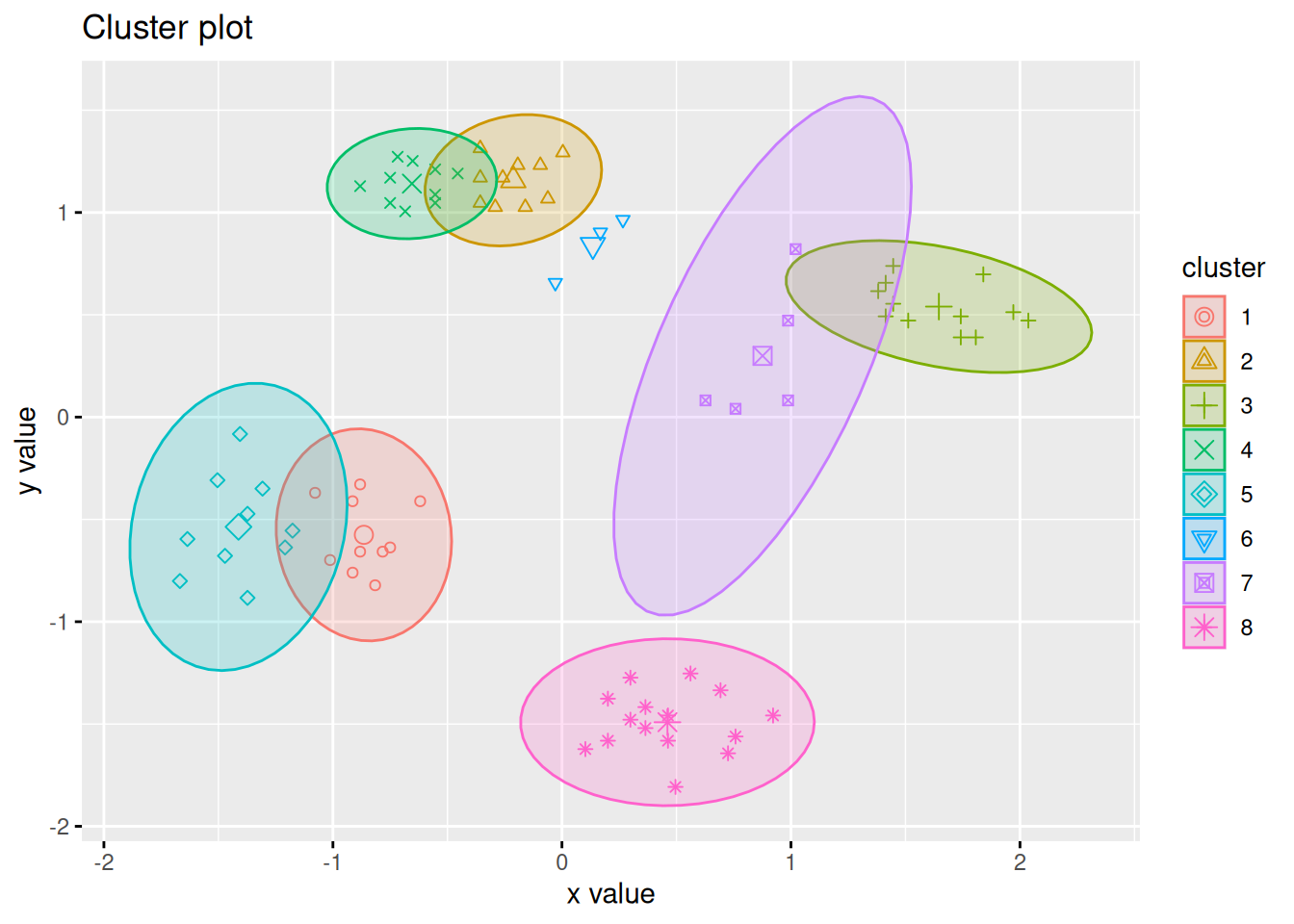

Note: The silhouette plot does not show correctly in R Studio if you have too many objects (bars are missing). I will work when you open a new plotting device with windows(), x11() or quartz().

ggplot visualization using factoextra

fviz_silhouette(silhouette(km$cluster, d))

##   cluster size ave.sil.width
## 1       1   23          0.75
## 2       2   17          0.68
## 3       3   15          0.81
## 4       4   20          0.72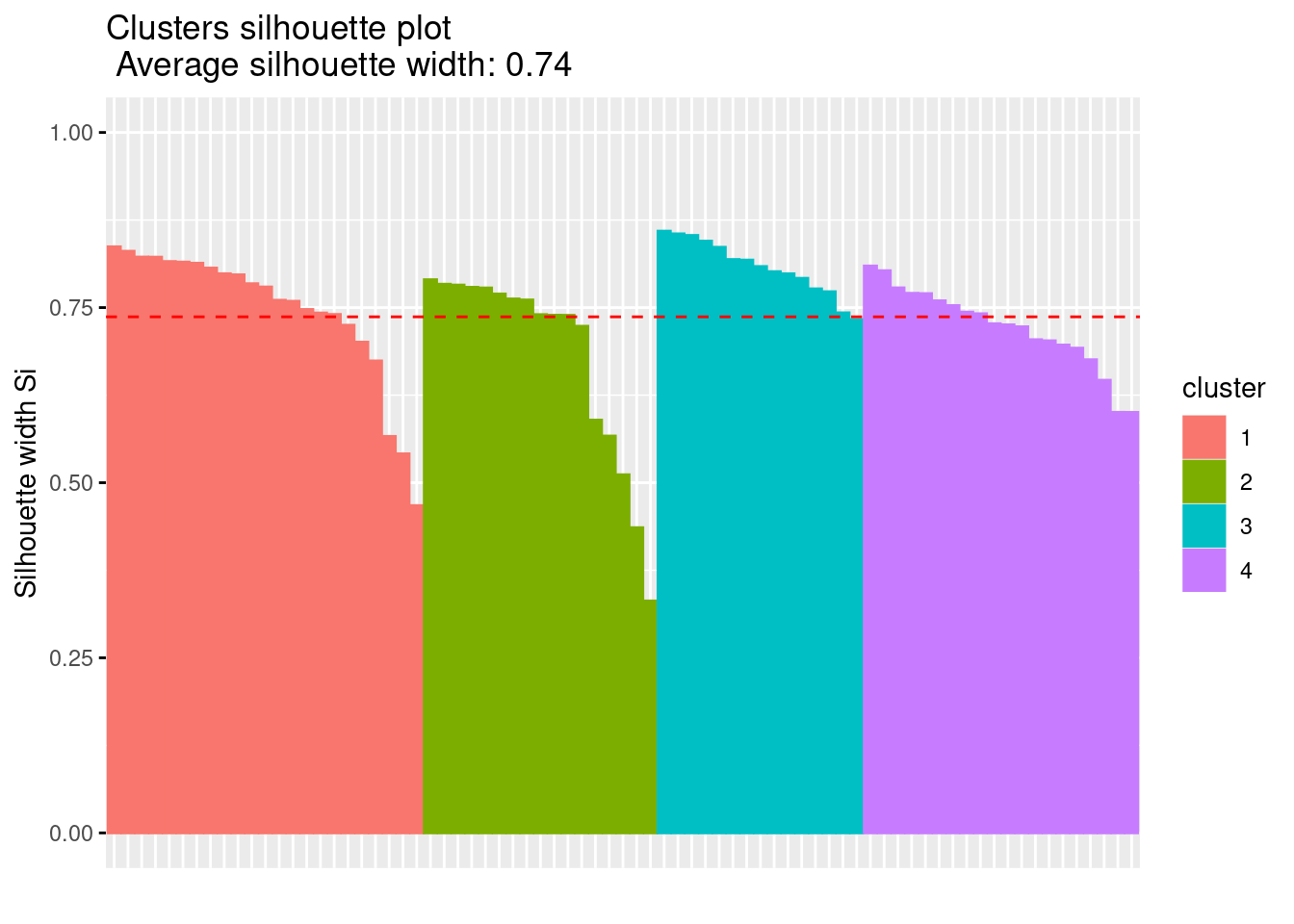

7.4.3 Find Optimal Number of Clusters for k-means

ggplot(ruspini_scaled, aes(x, y)) + geom_point()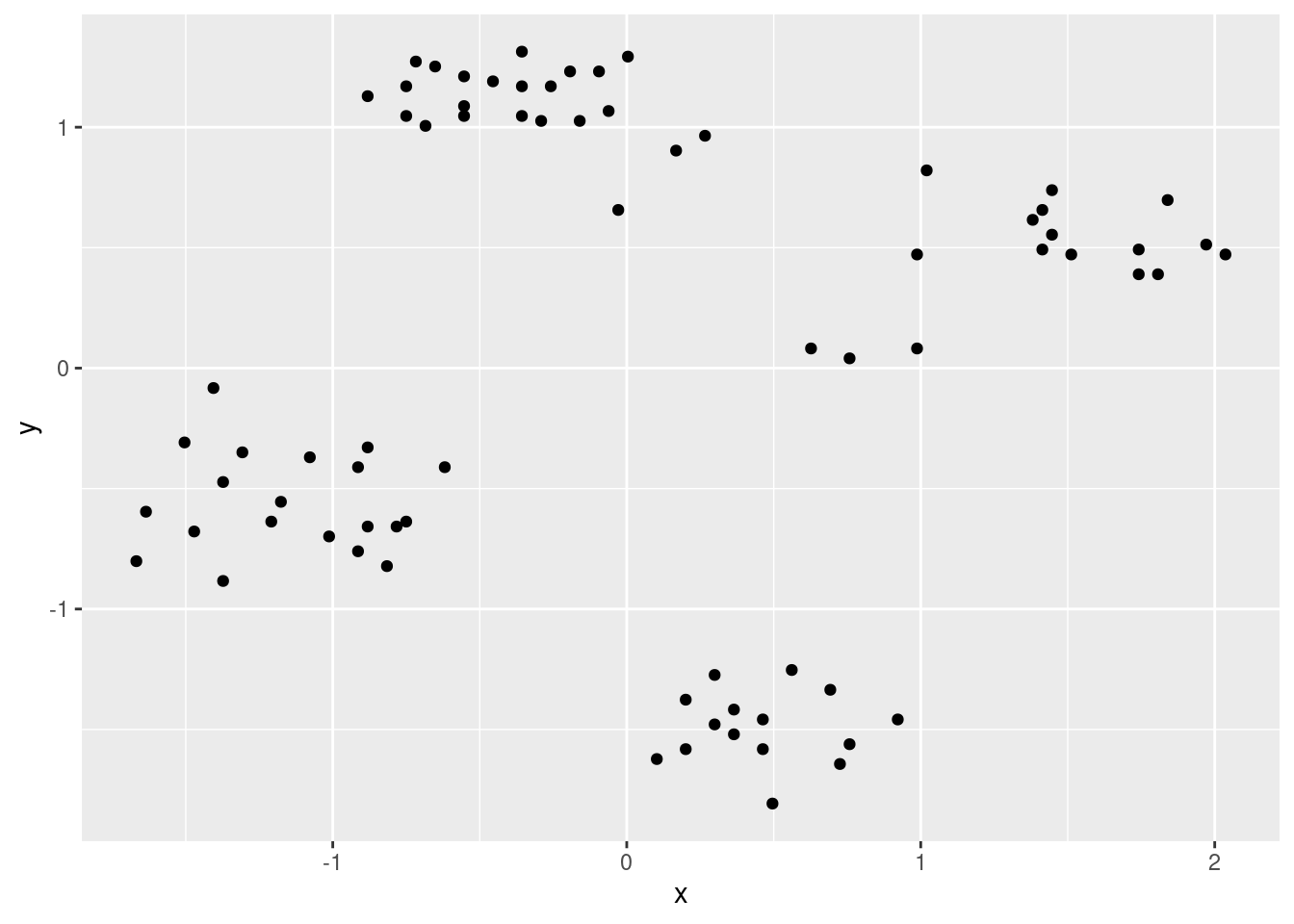

## We will use different methods and try 1-10 clusters.
set.seed(1234)
ks <- 2:10

7.4.3.1 Elbow Method: Within-Cluster Sum of Squares

Calculate the within-cluster sum of squares for different numbers of clusters and look for the knee or elbow in the plot. (nstart = 5 just repeats k-means 5 times and returns the best solution)

WCSS <- sapply(ks, FUN = function(k) {
  kmeans(ruspini_scaled, centers = k, nstart = 5)$tot.withinss
  })

ggplot(tibble(ks, WCSS), aes(ks, WCSS)) + geom_line() +
  geom_vline(xintercept = 4, color = "red", linetype = 2)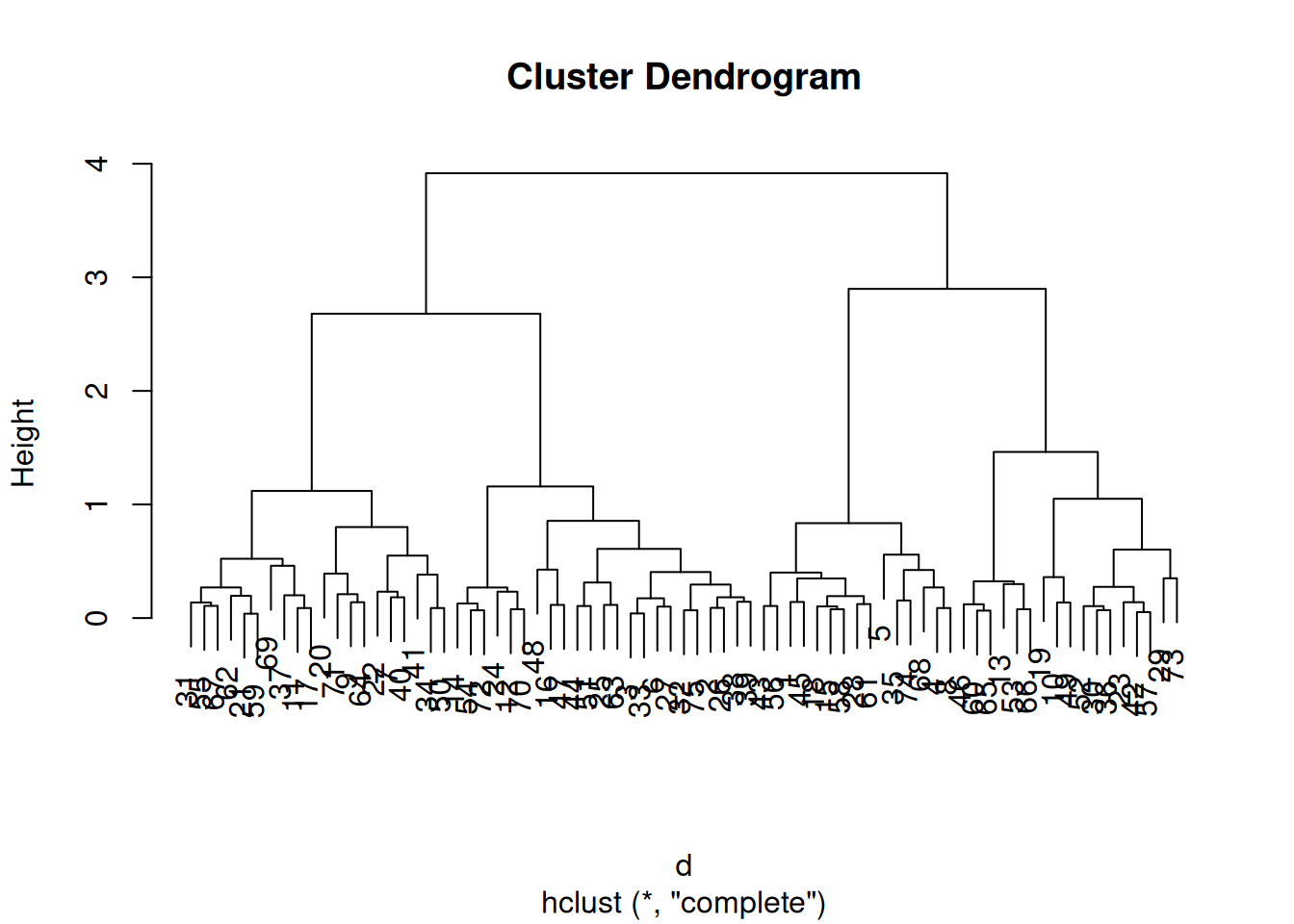

7.4.3.2 Average Silhouette Width

Plot the average silhouette width for different number of clusters and look for the maximum in the plot.

ASW <- sapply(ks, FUN=function(k) {
  fpc::cluster.stats(d, kmeans(ruspini_scaled, centers=k, nstart = 5)$cluster)$avg.silwidth
  })

best_k <- ks[which.max(ASW)]
best_k

## [1] 4

ggplot(tibble(ks, ASW), aes(ks, ASW)) + geom_line() +
  geom_vline(xintercept = best_k, color = "red", linetype = 2)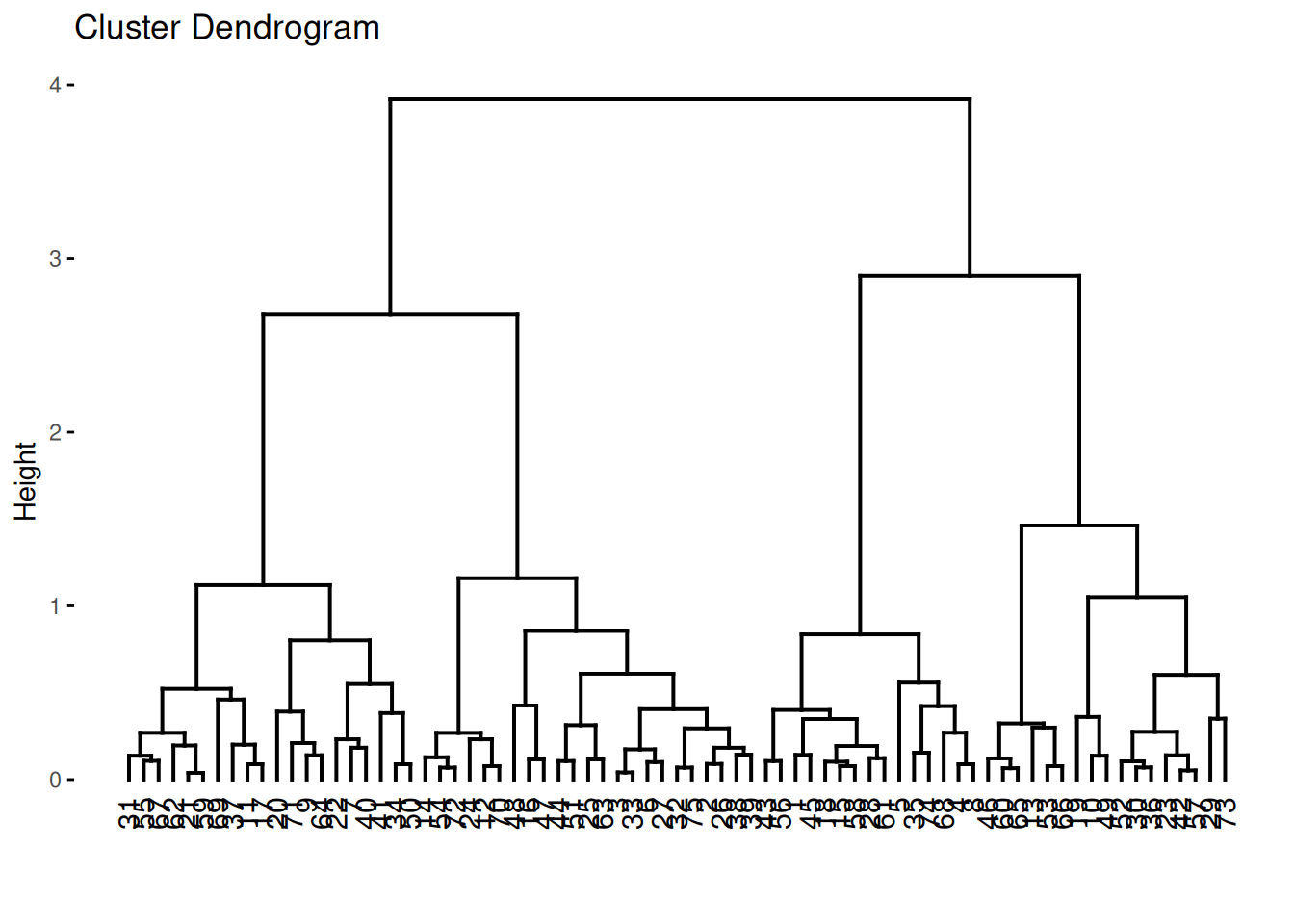

7.4.3.3 Dunn Index

Use Dunn index (another internal measure given by min. separation/ max. diameter)

DI <- sapply(ks, FUN=function(k) {
  fpc::cluster.stats(d, kmeans(ruspini_scaled, centers=k, nstart=5)$cluster)$dunn
})

best_k <- ks[which.max(DI)]
ggplot(tibble(ks, DI), aes(ks, DI)) + geom_line() +
  geom_vline(xintercept = best_k, color = "red", linetype = 2)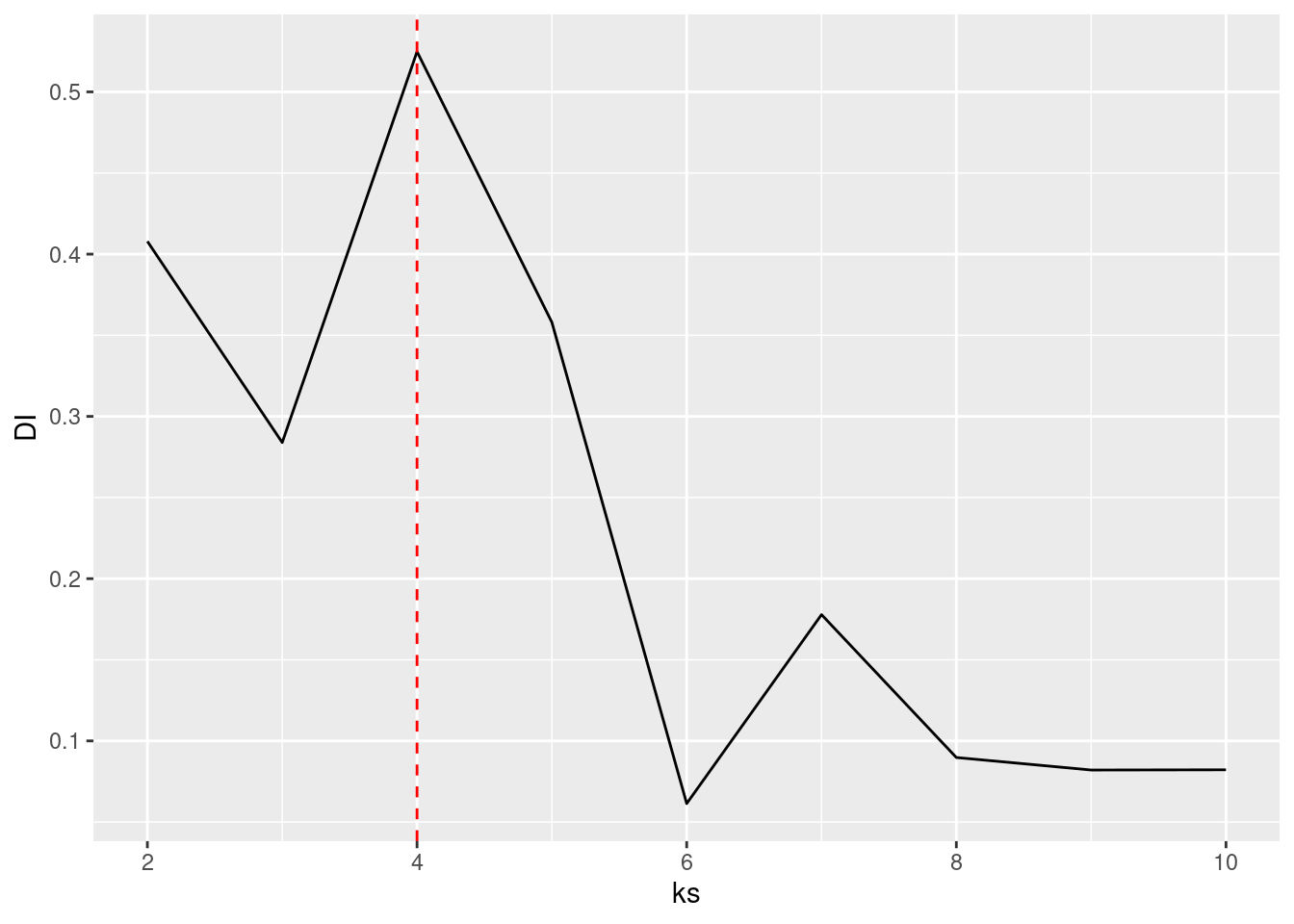

7.4.3.4 Gap Statistic

Compares the change in within-cluster dispersion with that expected from a null model (see ? clusGap). The default method is to choose the smallest k such that its value Gap(k) is not more than 1 standard error away from the first local maximum.

library(cluster)
k <- clusGap(ruspini_scaled, FUN = kmeans,  nstart = 10, K.max = 10)
k

## Clustering Gap statistic ["clusGap"] from call:
## clusGap(x = ruspini_scaled, FUNcluster = kmeans, K.max = 10, nstart = 10)
## B=100 simulated reference sets, k = 1..10; spaceH0="scaledPCA"
##  --> Number of clusters (method 'firstSEmax', SE.factor=1): 4
##       logW E.logW     gap SE.sim
##  [1,] 3.50   3.47 -0.0308 0.0357
##  [2,] 3.07   3.15  0.0762 0.0374
##  [3,] 2.68   2.90  0.2247 0.0380
##  [4,] 2.11   2.70  0.5971 0.0363
##  [5,] 1.99   2.57  0.5827 0.0347
##  [6,] 1.86   2.45  0.5871 0.0365
##  [7,] 1.73   2.35  0.6156 0.0395
##  [8,] 1.64   2.26  0.6157 0.0413
##  [9,] 1.56   2.17  0.6113 0.0409
## [10,] 1.51   2.09  0.5799 0.0393

plot(k)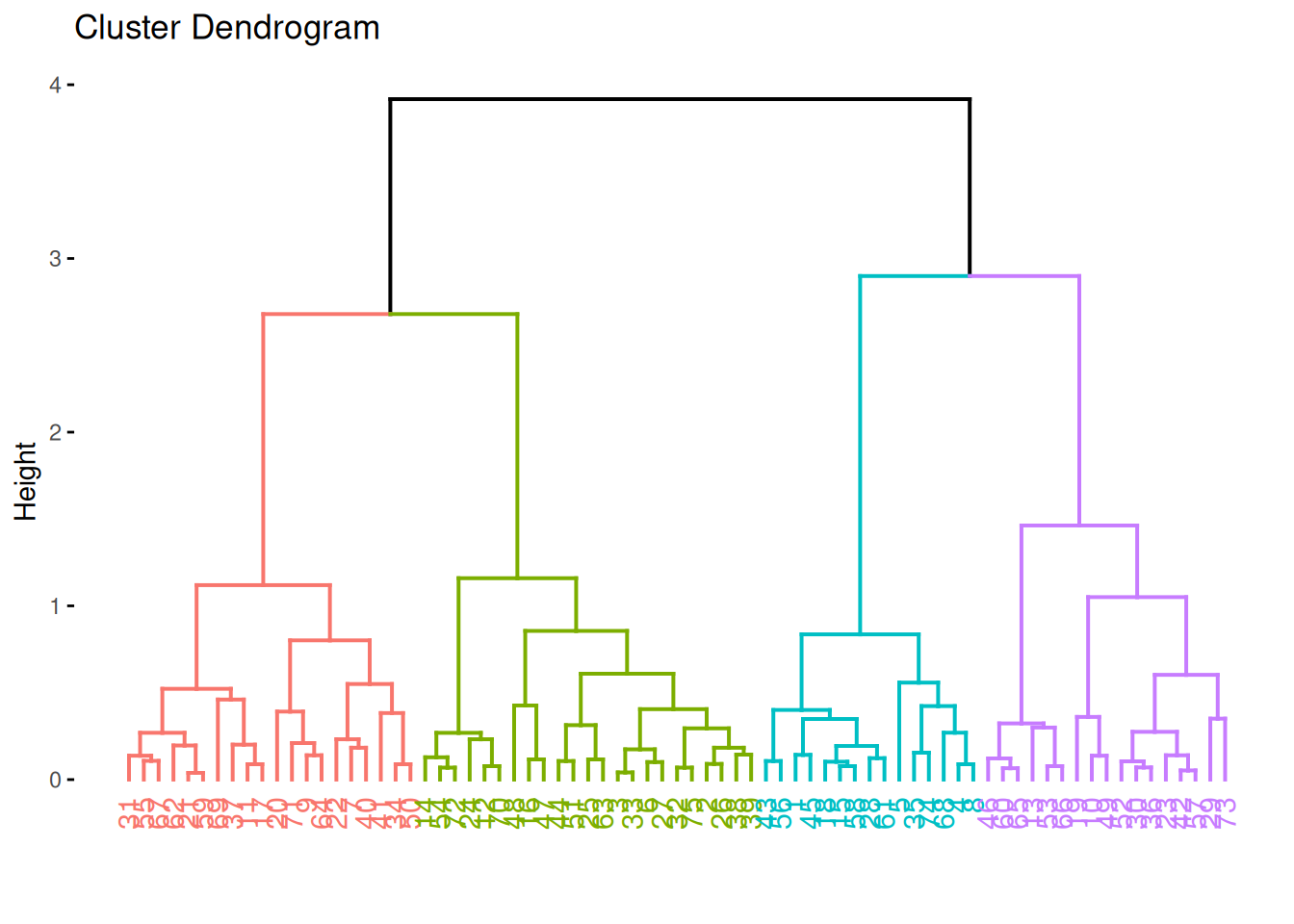

Note: these methods can also be used for hierarchical clustering.

There have been many other methods and indices proposed to determine the number of clusters. See, e.g., package NbClust.

7.4.4 Visualizing the Distance Matrix

ggplot(ruspini_scaled, aes(x, y, color = factor(km$cluster))) + geom_point()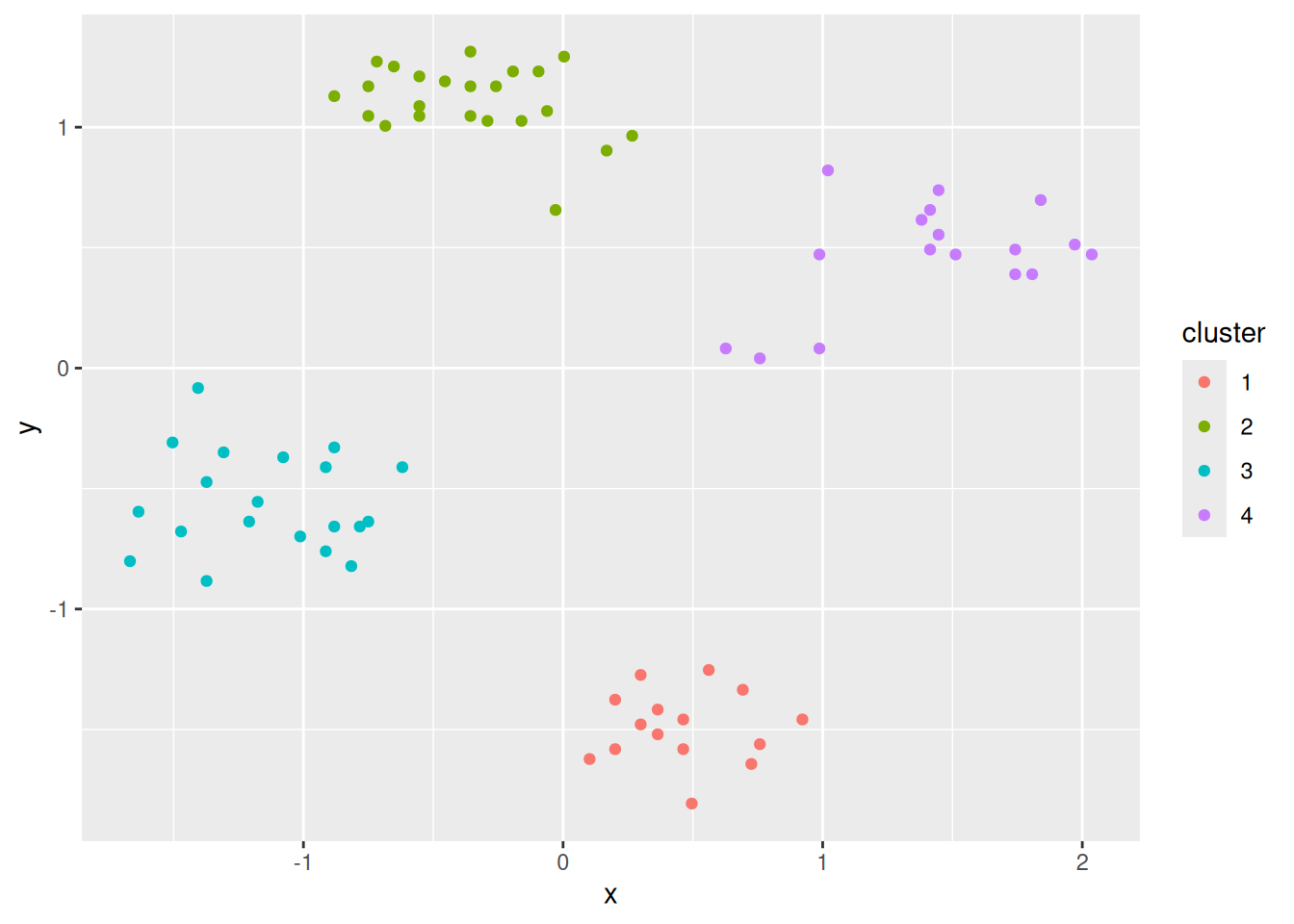

d <- dist(ruspini_scaled)

Inspect the distance matrix between the first 5 objects.

as.matrix(d)[1:5, 1:5]

##       1     2    3     4     5
## 1 0.000 0.227 1.07 3.429 2.750
## 2 0.227 0.000 1.05 3.338 2.697
## 3 1.074 1.052 0.00 2.399 1.680
## 4 3.429 3.338 2.40 0.000 0.853
## 5 2.750 2.697 1.68 0.853 0.000

A false-color image visualizes each value in the matrix as a pixel with the color representing the value.

library(seriation)
pimage(d, col = bluered(100))

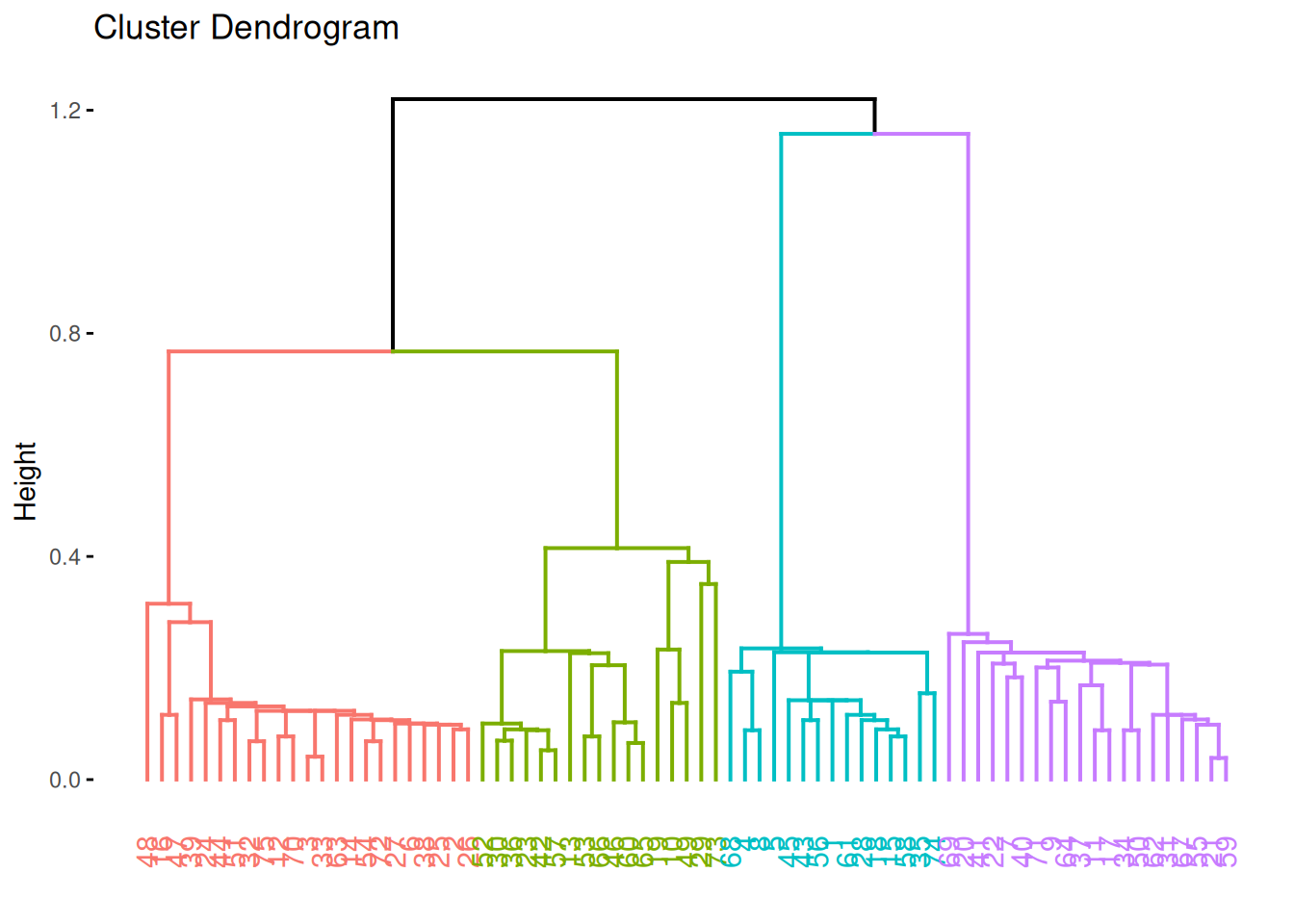
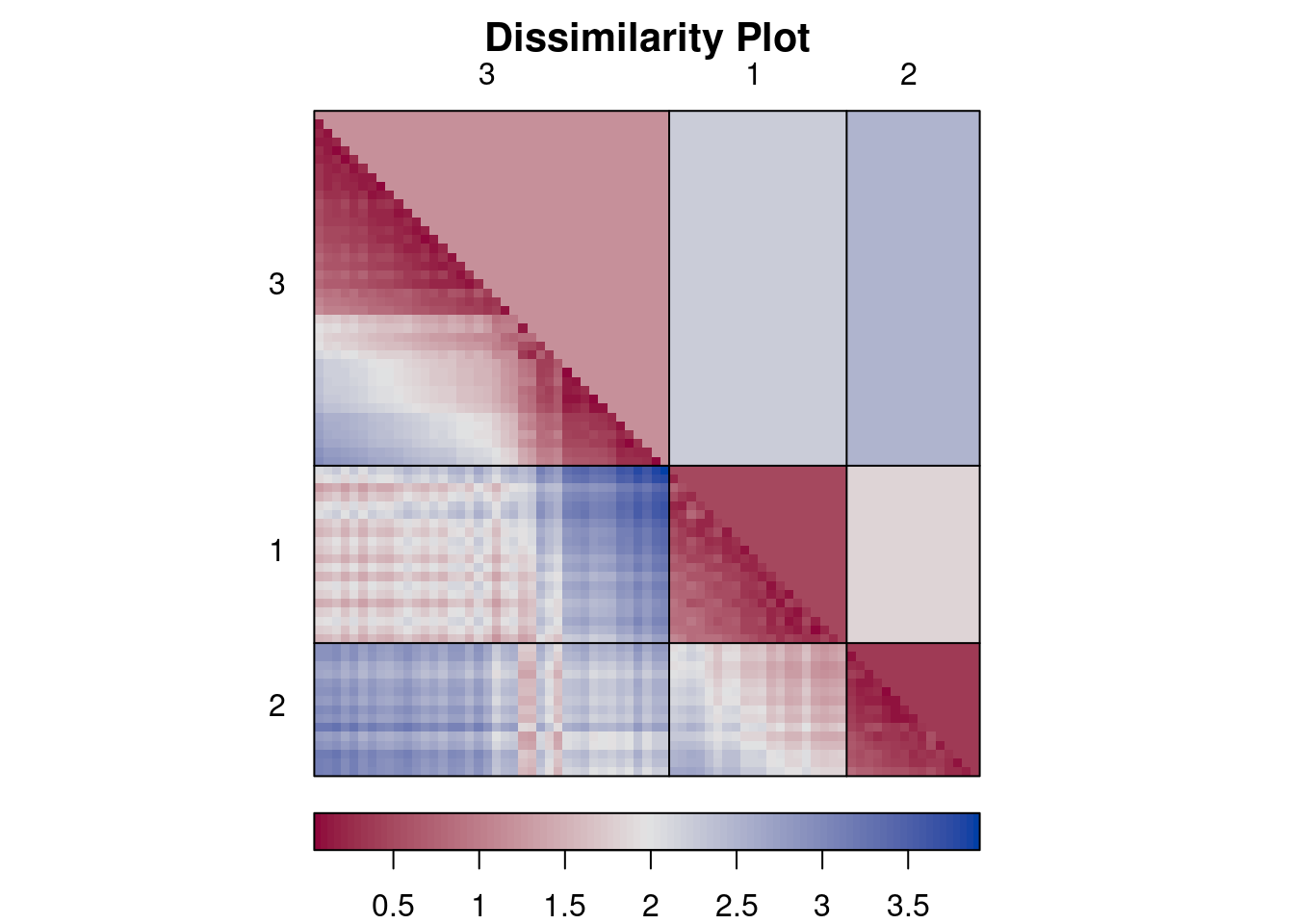
Rows and columns are the objects as they are ordered in the data set. The diagonal represents the distance between an object and itself and has by definition a distance of 0 (dark line). Visualizing the unordered distance matrix does not show much structure, but we can reorder the matrix (rows and columns) using the k-means cluster labels from cluster 1 to 4. A clear block structure representing the clusters becomes visible.

pimage(d, order=order(km$cluster), col = bluered(100))

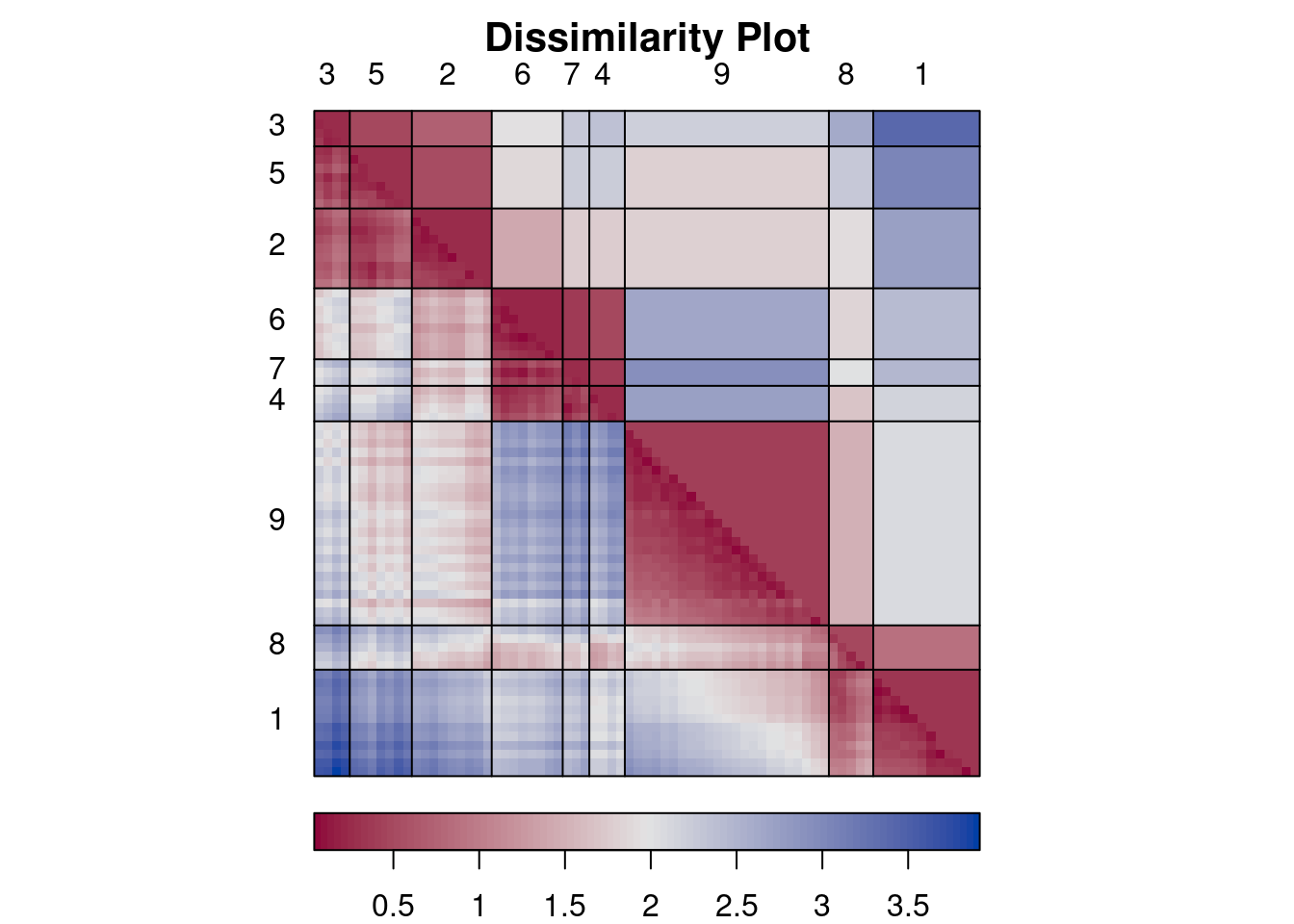
Plot function dissplot in package seriation rearranges the matrix and adds lines and cluster labels. In the lower half of the plot, it shows average dissimilarities between clusters. The function organizes the objects by cluster and then reorders clusters and objects within clusters so that more similar objects are closer together.

dissplot(d, labels = km$cluster, options = list(main = "k-means with k=4"))

The reordering by dissplot makes the misspecification of k visible as blocks.

dissplot(d, labels = kmeans(ruspini_scaled, centers = 3)$cluster, col = bluered(100))

dissplot(d, labels = kmeans(ruspini_scaled, centers = 9)$cluster, col = bluered(100))

Using factoextra

fviz_dist(d)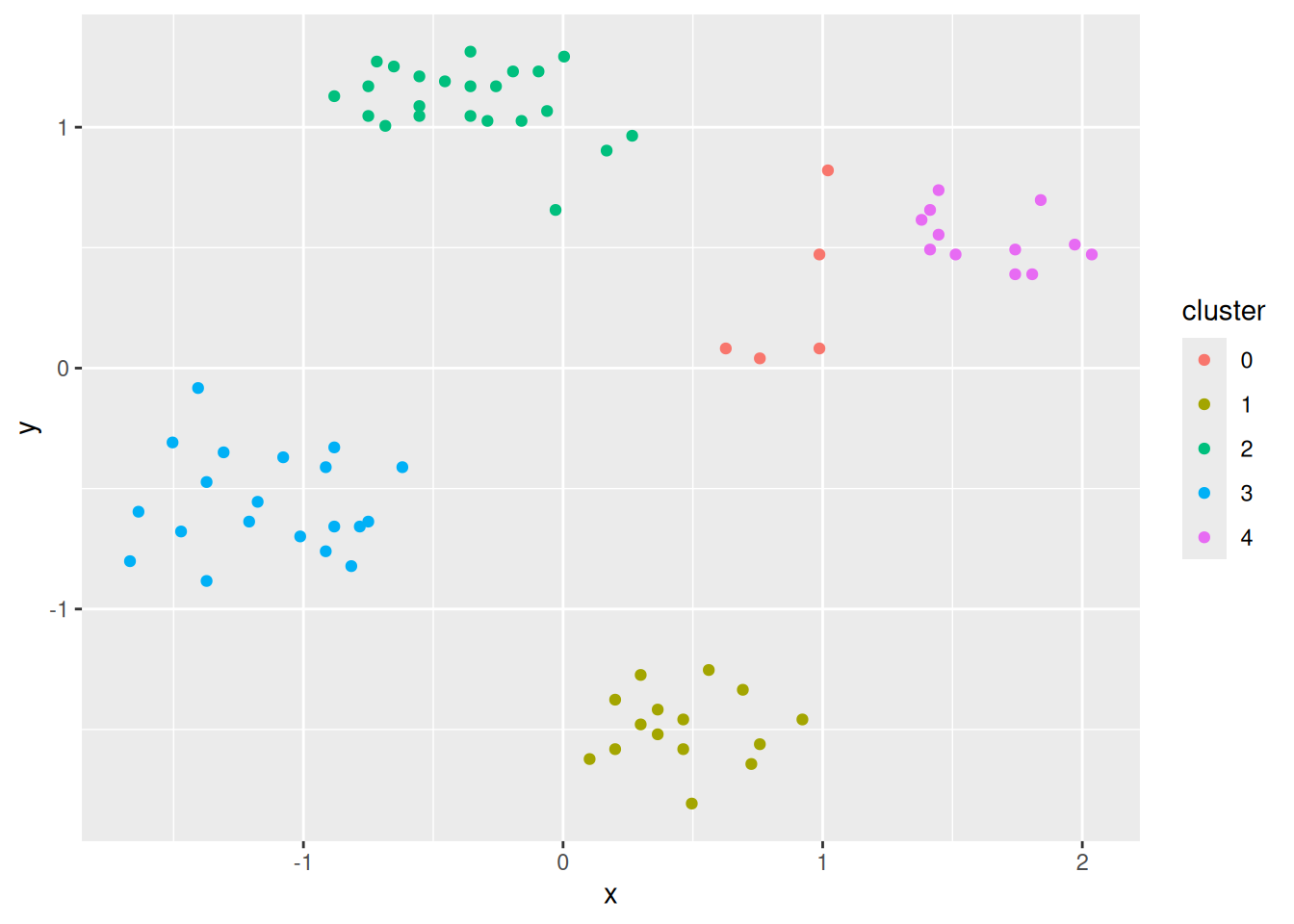

7.5 External Cluster Validation

External cluster validation uses ground truth information. That is, the user has an idea how the data should be grouped. This could be a known class label not provided to the clustering algorithm.

We use an artificial data set with known groups.

library(mlbench)
set.seed(1234)
shapes <- mlbench.smiley(n = 500, sd1 = 0.1, sd2 = 0.05)
plot(shapes)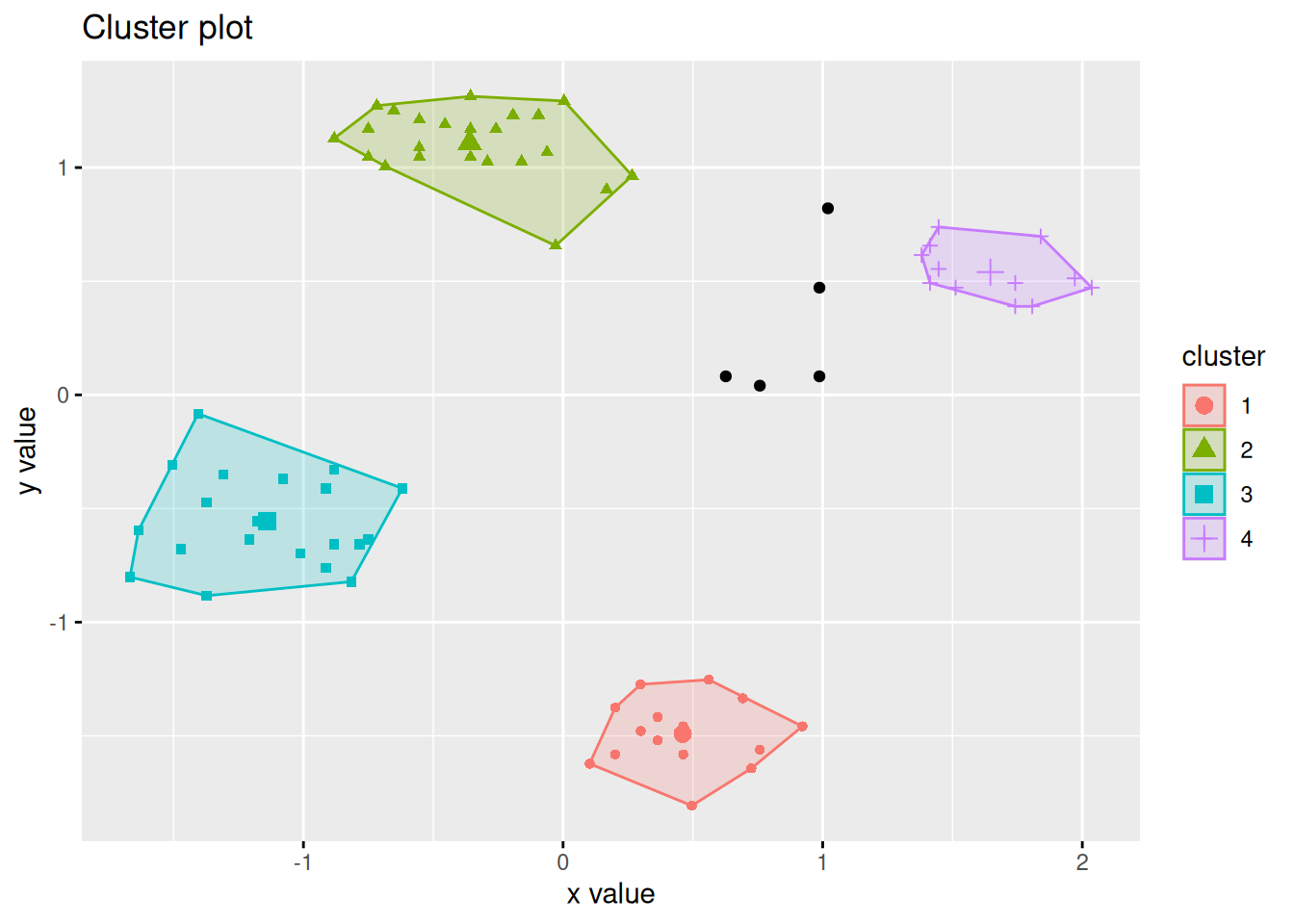

Prepare data

truth <- as.integer(shapes$class)
shapes <- shapes$x
colnames(shapes) <- c("x", "y")

shapes <- shapes |> scale() |> as_tibble()

ggplot(shapes, aes(x, y)) + geom_point()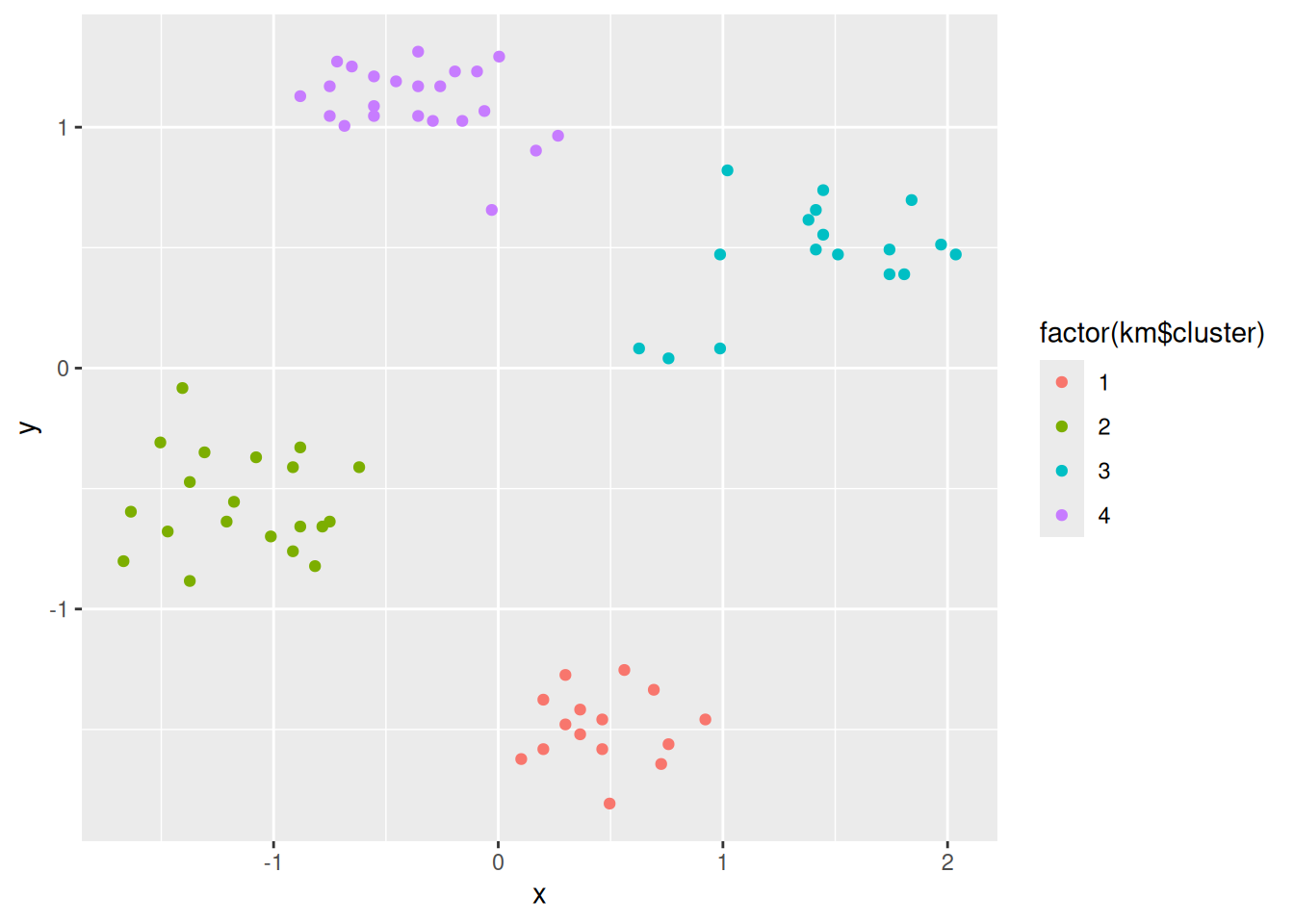

Find optimal number of Clusters for k-means

ks <- 2:20

Use within sum of squares (look for the knee)

WCSS <- sapply(ks, FUN = function(k) {
  kmeans(shapes, centers = k, nstart = 10)$tot.withinss
})

ggplot(tibble(ks, WCSS), aes(ks, WCSS)) + geom_line()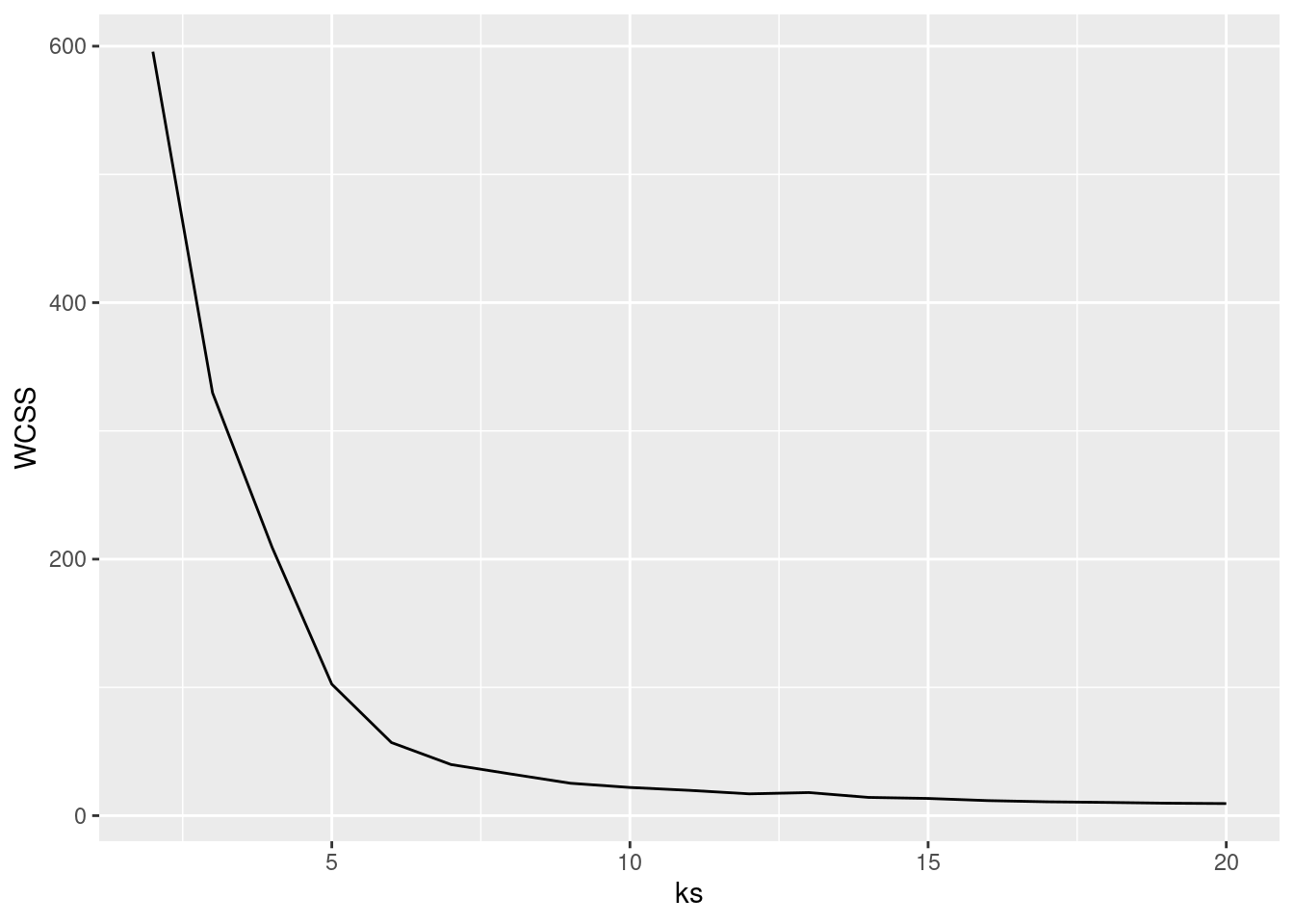

Looks like it could be 7 clusters

km <- kmeans(shapes, centers = 7, nstart = 10)

ggplot(shapes |> add_column(cluster = factor(km$cluster)), aes(x, y, color = cluster)) +
  geom_point()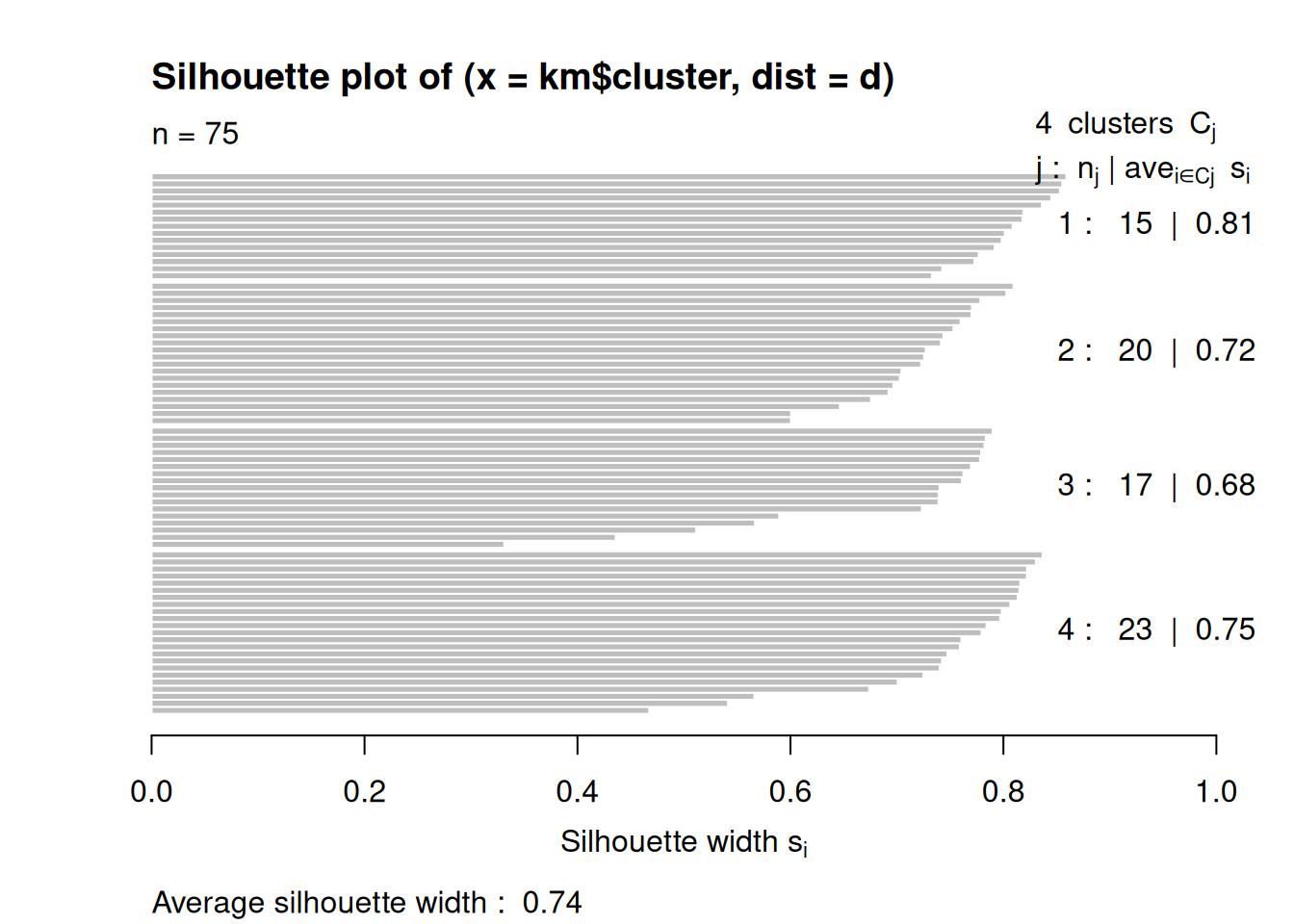

Hierarchical clustering: We use single-link because of the mouth is non-convex and chaining may help.

d <- dist(shapes)
hc <- hclust(d, method = "single")

Find optimal number of clusters

ASW <- sapply(ks, FUN = function(k) {
  fpc::cluster.stats(d, cutree(hc, k))$avg.silwidth
})

ggplot(tibble(ks, ASW), aes(ks, ASW)) + geom_line()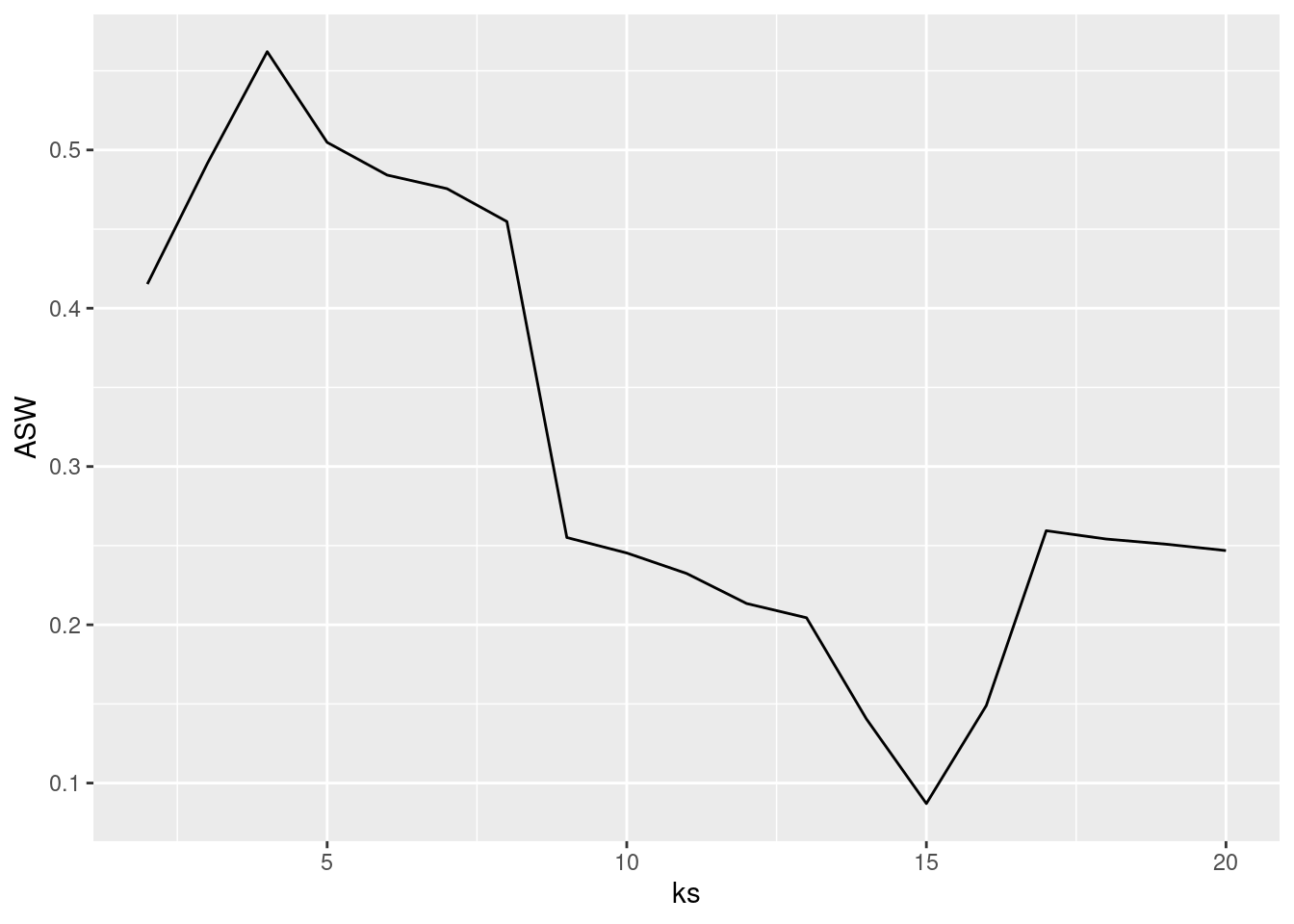

The maximum is clearly at 4 clusters.

hc_4 <- cutree(hc, 4)

ggplot(shapes |> add_column(cluster = factor(hc_4)), aes(x, y, color = cluster)) +
  geom_point()

Compare with ground truth with the corrected (=adjusted) Rand index (ARI), the variation of information (VI) index, entropy and purity.

cluster_stats computes ARI and VI as comparative measures. I define functions for entropy and purity here:

entropy <- function(cluster, truth) {
  k <- max(cluster, truth)
  cluster <- factor(cluster, levels = 1:k)
  truth <- factor(truth, levels = 1:k)
  w <- table(cluster)/length(cluster)

  cnts <- sapply(split(truth, cluster), table)
  p <- sweep(cnts, 1, rowSums(cnts), "/")
  p[is.nan(p)] <- 0
  e <- -p * log(p, 2)

  sum(w * rowSums(e, na.rm = TRUE))
}

purity <- function(cluster, truth) {
  k <- max(cluster, truth)
  cluster <- factor(cluster, levels = 1:k)
  truth <- factor(truth, levels = 1:k)
  w <- table(cluster)/length(cluster)

  cnts <- sapply(split(truth, cluster), table)
  p <- sweep(cnts, 1, rowSums(cnts), "/")
  p[is.nan(p)] <- 0

  sum(w * apply(p, 1, max))
}

calculate measures (for comparison we also use random “clusterings” with 4 and 6 clusters)

random_4 <- sample(1:4, nrow(shapes), replace = TRUE)
random_6 <- sample(1:6, nrow(shapes), replace = TRUE)

r <- rbind(
  kmeans_7 = c(
    unlist(fpc::cluster.stats(d, km$cluster, truth, compareonly = TRUE)),
    entropy = entropy(km$cluster, truth),
    purity = purity(km$cluster, truth)
    ),
  hc_4 = c(
    unlist(fpc::cluster.stats(d, hc_4, truth, compareonly = TRUE)),
    entropy = entropy(hc_4, truth),
    purity = purity(hc_4, truth)
    ),
  random_4 = c(
    unlist(fpc::cluster.stats(d, random_4, truth, compareonly = TRUE)),
    entropy = entropy(random_4, truth),
    purity = purity(random_4, truth)
    ),
  random_6 = c(
    unlist(fpc::cluster.stats(d, random_6, truth, compareonly = TRUE)),
    entropy = entropy(random_6, truth),
    purity = purity(random_6, truth)
    )
  )
r

##          corrected.rand    vi entropy purity
## kmeans_7        0.63823 0.571   0.229  0.464
## hc_4            1.00000 0.000   0.000  1.000
## random_4       -0.00324 2.683   1.988  0.288
## random_6       -0.00213 3.076   1.728  0.144

Notes:

Hierarchical clustering found the perfect clustering.
Entropy and purity are heavily impacted by the number of clusters (more clusters improve the metric).
The corrected rand index shows clearly that the random clusterings have no relationship with the ground truth (very close to 0). This is a very helpful property.

Read ? cluster.stats for an explanation of all the available indices.

7.6 Advanced Data Preparation for Clustering

7.6.1 Outlier Removal

Most clustering algorithms perform complete assignment (i.e., all data points need to be assigned to a cluster). Outliers will affect the clustering. It is useful to identify outliers and remove strong outliers prior to clustering. A density based method to identify outlier is LOF (Local Outlier Factor). It is related to dbscan and compares the density around a point with the densities around its neighbors (you have to specify the neighborhood size $k$). The LOF value for a regular data point is 1. The larger the LOF value gets, the more likely the point is an outlier.

library(dbscan)

Add a clear outlier to the scaled Ruspini dataset that is 10 standard deviations above the average for the x axis.

ruspini_scaled_outlier <- ruspini_scaled |> add_case(x=10,y=0)

7.6.1.1 Visual inspection of the data

Outliers can be identified using summary statistics, histograms, scatterplots (pairs plots), and boxplots, etc. We use here a pairs plot (the diagonal contains smoothed histograms). The outlier is visible as the single separate point in the scatter plot and as the long tail of the smoothed histogram for x (we would expect most observations to fall in the range \[-3,3\] in normalized data).

library("GGally")
ggpairs(ruspini_scaled_outlier, progress = FALSE)

The outlier is a problem for k-means

km <- kmeans(ruspini_scaled_outlier, centers = 4, nstart = 10)
ruspini_scaled_outlier_km <- ruspini_scaled_outlier|>
  add_column(cluster = factor(km$cluster))
centroids <- as_tibble(km$centers, rownames = "cluster")

ggplot(ruspini_scaled_outlier_km, aes(x = x, y = y, color = cluster)) + geom_point() +
  geom_point(data = centroids, aes(x = x, y = y, color = cluster), shape = 3, size = 10)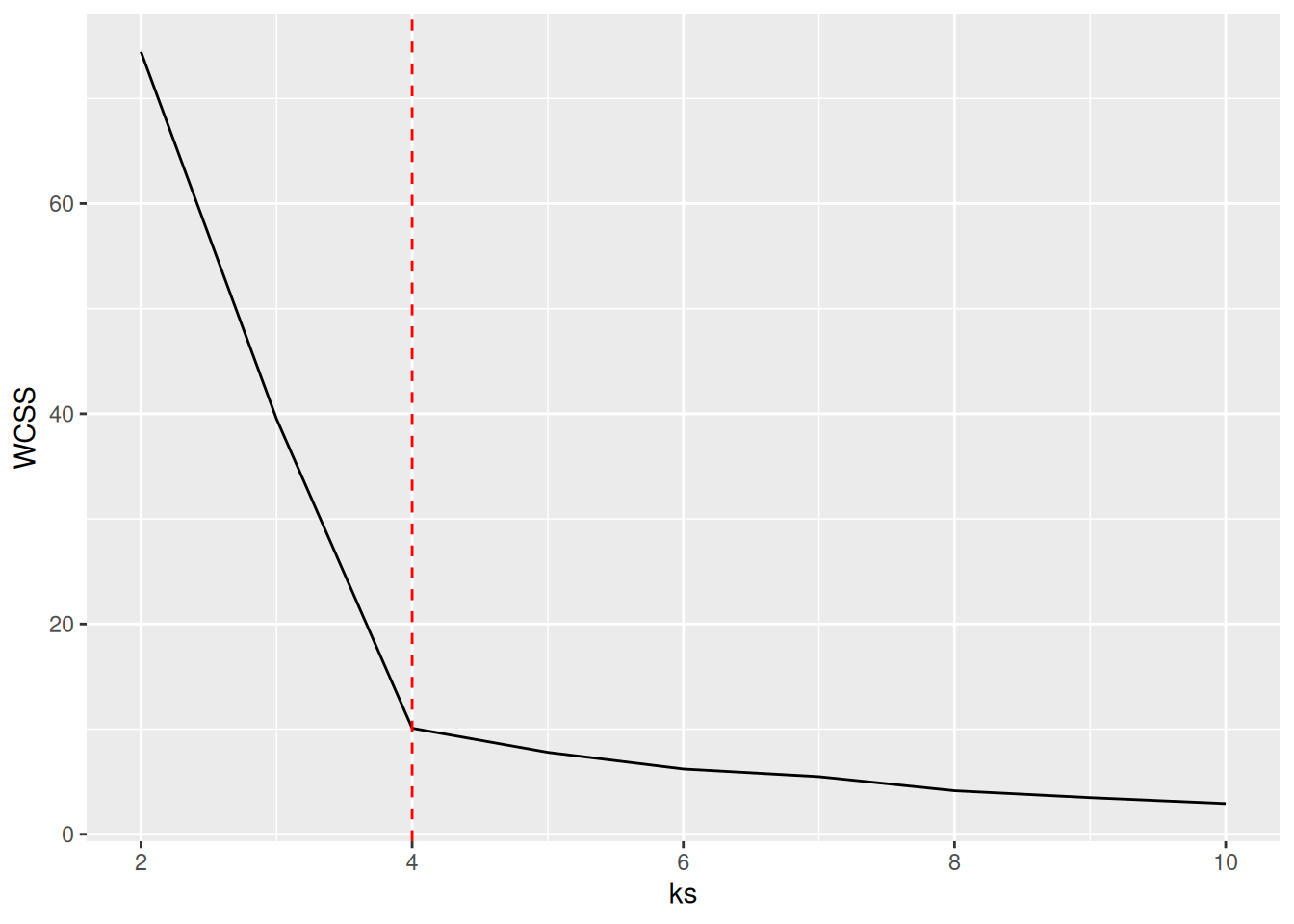

This problem can be fixed by increasing the number of clusters and removing small clusters in a post-processing step or by identifying and removing outliers before clustering.

7.6.1.2 Local Outlier Factor (LOF)

The Local Outlier Factor is related to concepts of DBSCAN can help to identify potential outliers. Calculate the LOF (I choose a local neighborhood size of 10 for density estimation),

lof <- lof(ruspini_scaled_outlier, minPts= 10)
lof

##  [1]  1.084  1.006  1.368  1.212  1.083  1.175  0.978
##  [8]  0.998  0.972  0.965  0.990  1.041  1.051  1.252
## [15]  1.026  0.938  1.020  1.024  1.572  1.068  1.209
## [22]  1.070  1.138  1.002  0.996  1.598  1.034  1.071
## [29]  1.015  0.939  1.626  0.976  0.997  1.083  1.021
## [36]  1.040  1.021  1.209  1.088  0.981  0.932  1.013
## [43]  1.397  0.994  1.160  0.941  0.993  0.943  0.933
## [50]  1.494  1.021  1.006  0.992  0.954  1.085  1.143
## [57]  0.982  1.020  0.986  0.918  1.034  1.104  1.004
## [64]  1.041  0.983  1.039  0.985  1.019  0.963  1.059
## [71]  1.001  0.934  1.051  1.023  0.977 17.899

ggplot(ruspini_scaled_outlier |> add_column(lof = lof), aes(x, y, color = lof)) +
    geom_point() + scale_color_gradient(low = "gray", high = "red")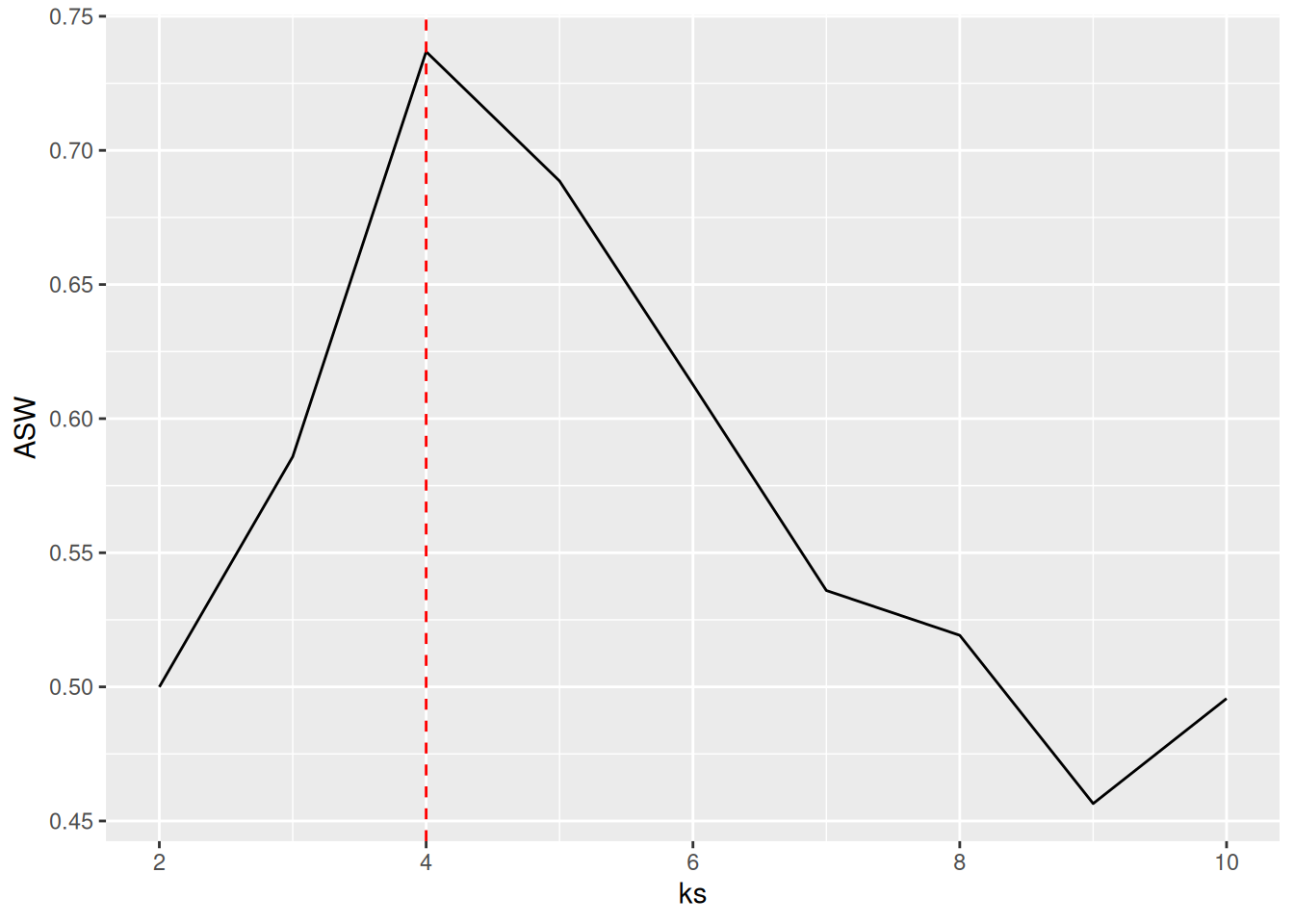

Plot the points sorted by increasing LOF and look for a knee.

ggplot(tibble(index = seq_len(length(lof)), lof = sort(lof)), aes(index, lof)) +
  geom_line() +
  geom_hline(yintercept = 1, color = "red", linetype = 2)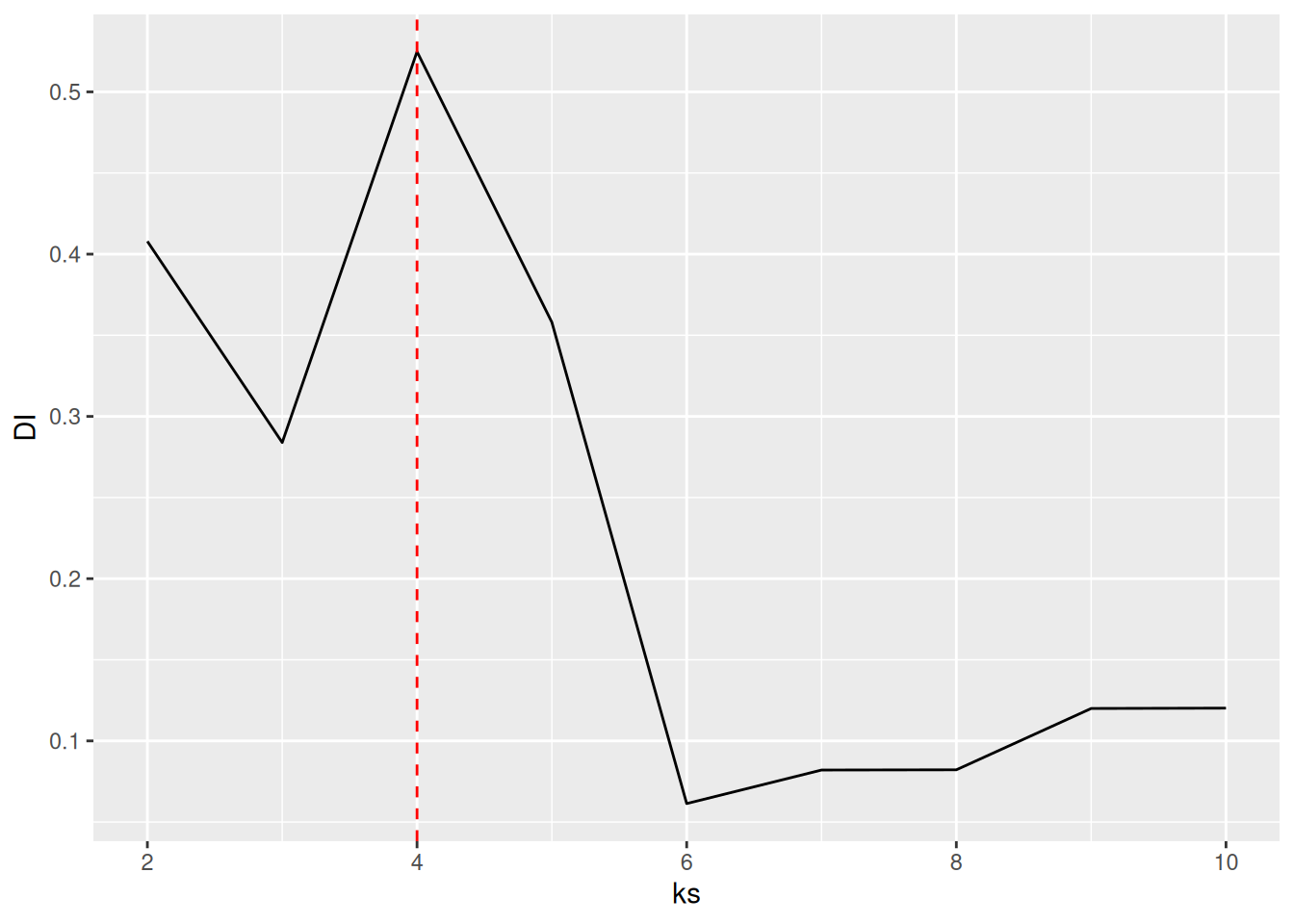

Choose a threshold above 1.

ggplot(ruspini_scaled_outlier |> add_column(outlier = lof >= 2), aes(x, y, color = outlier)) +
  geom_point()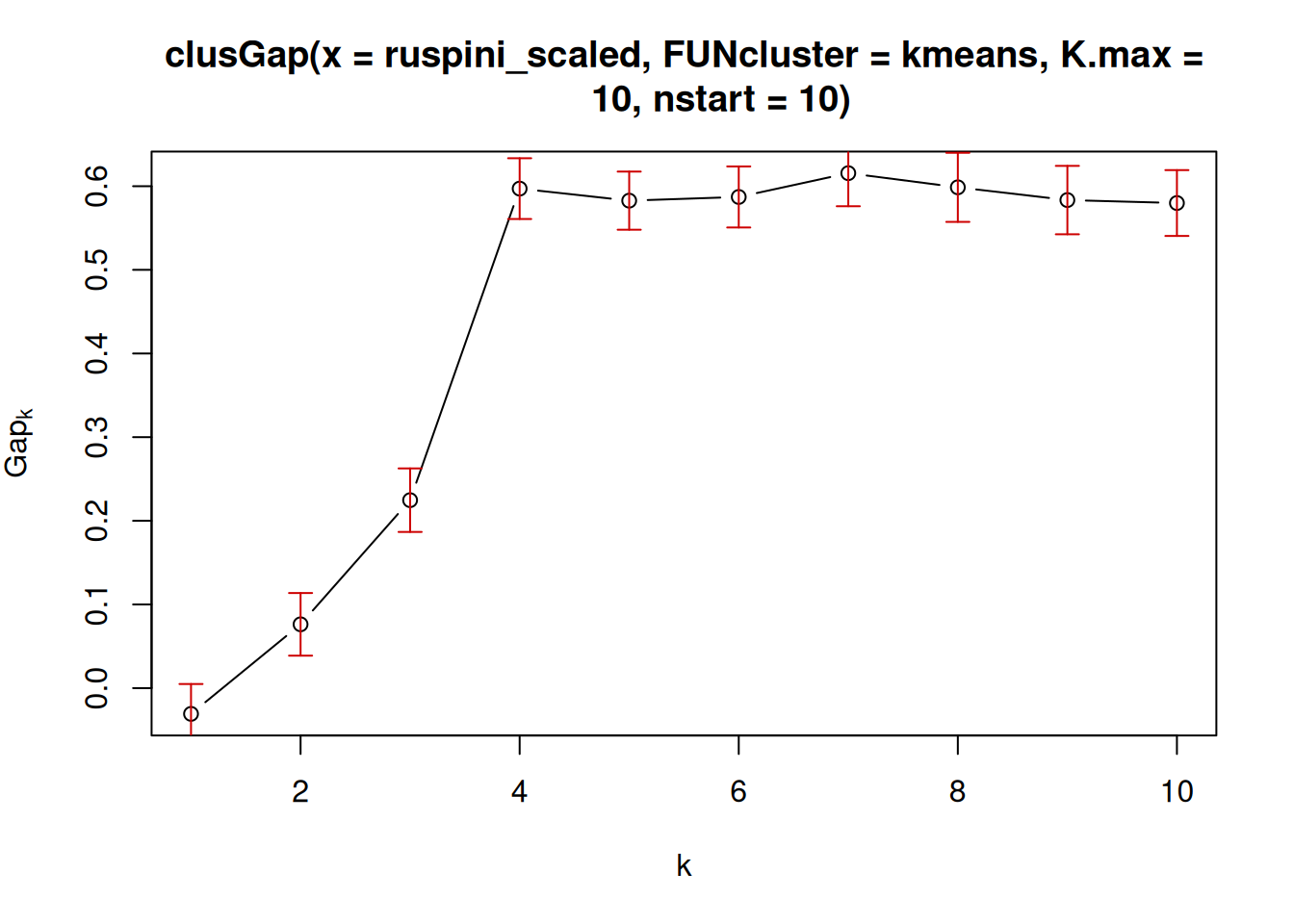

Analyze the found outliers (they might be interesting data points) and then cluster the data without them.

ruspini_scaled_clean <- ruspini_scaled_outlier  |> filter(lof < 2)

km <- kmeans(ruspini_scaled_clean, centers = 4, nstart = 10)
ruspini_scaled_clean_km <- ruspini_scaled_clean|>
  add_column(cluster = factor(km$cluster))
centroids <- as_tibble(km$centers, rownames = "cluster")

ggplot(ruspini_scaled_clean_km, aes(x = x, y = y, color = cluster)) + geom_point() +
  geom_point(data = centroids, aes(x = x, y = y, color = cluster), shape = 3, size = 10)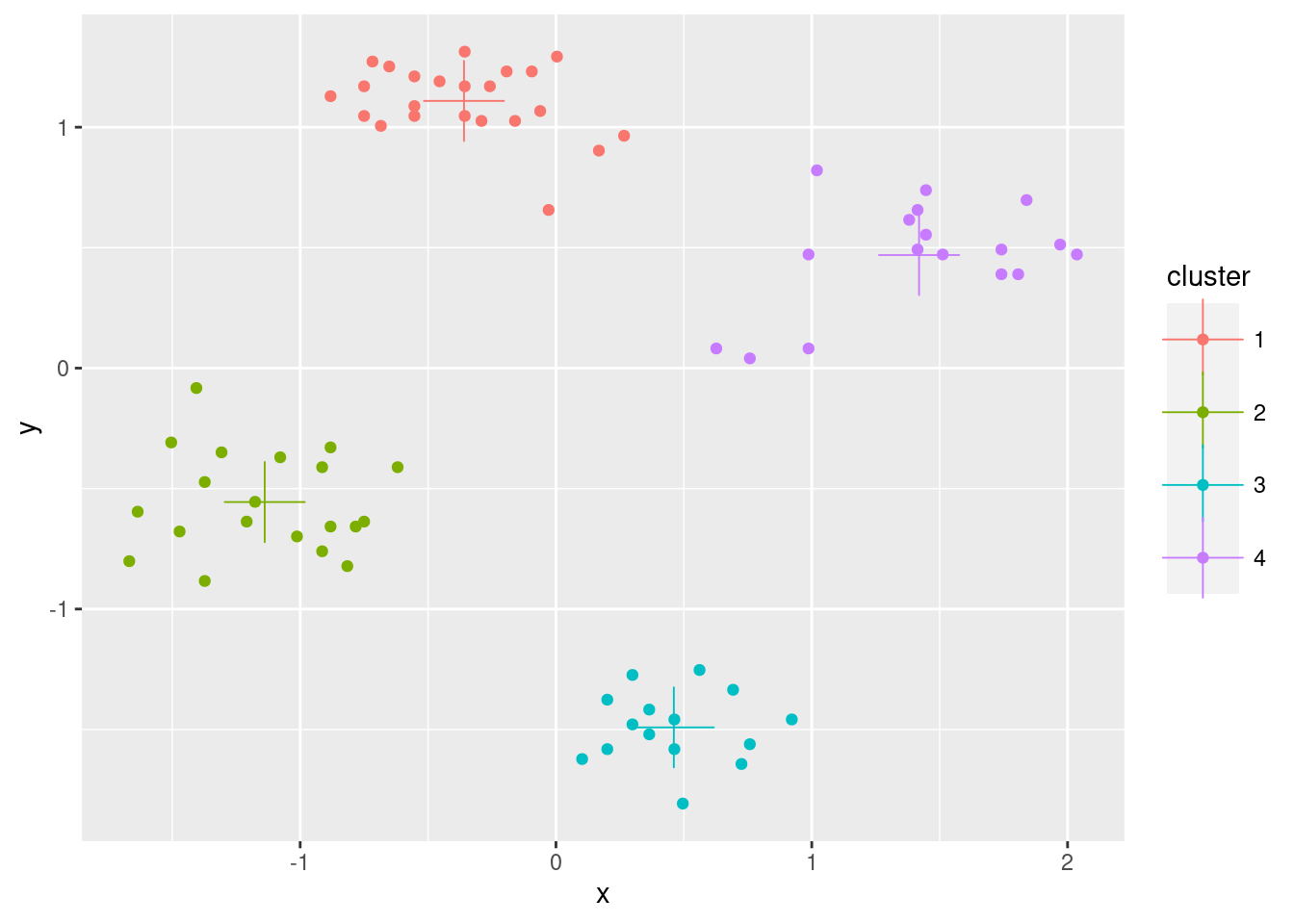

There are many other outlier removal strategies available. See, e.g., package outliers.

7.6.2 Clustering Tendency

Most clustering algorithms will always produce a clustering, even if the data does not contain a cluster structure. It is typically good to check cluster tendency before attempting to cluster the data.

We use again the smiley data.

library(mlbench)
shapes <- mlbench.smiley(n = 500, sd1 = 0.1, sd2 = 0.05)$x
colnames(shapes) <- c("x", "y")
shapes <- as_tibble(shapes)

7.6.2.1 Scatter plots

The first step is visual inspection using scatter plots.

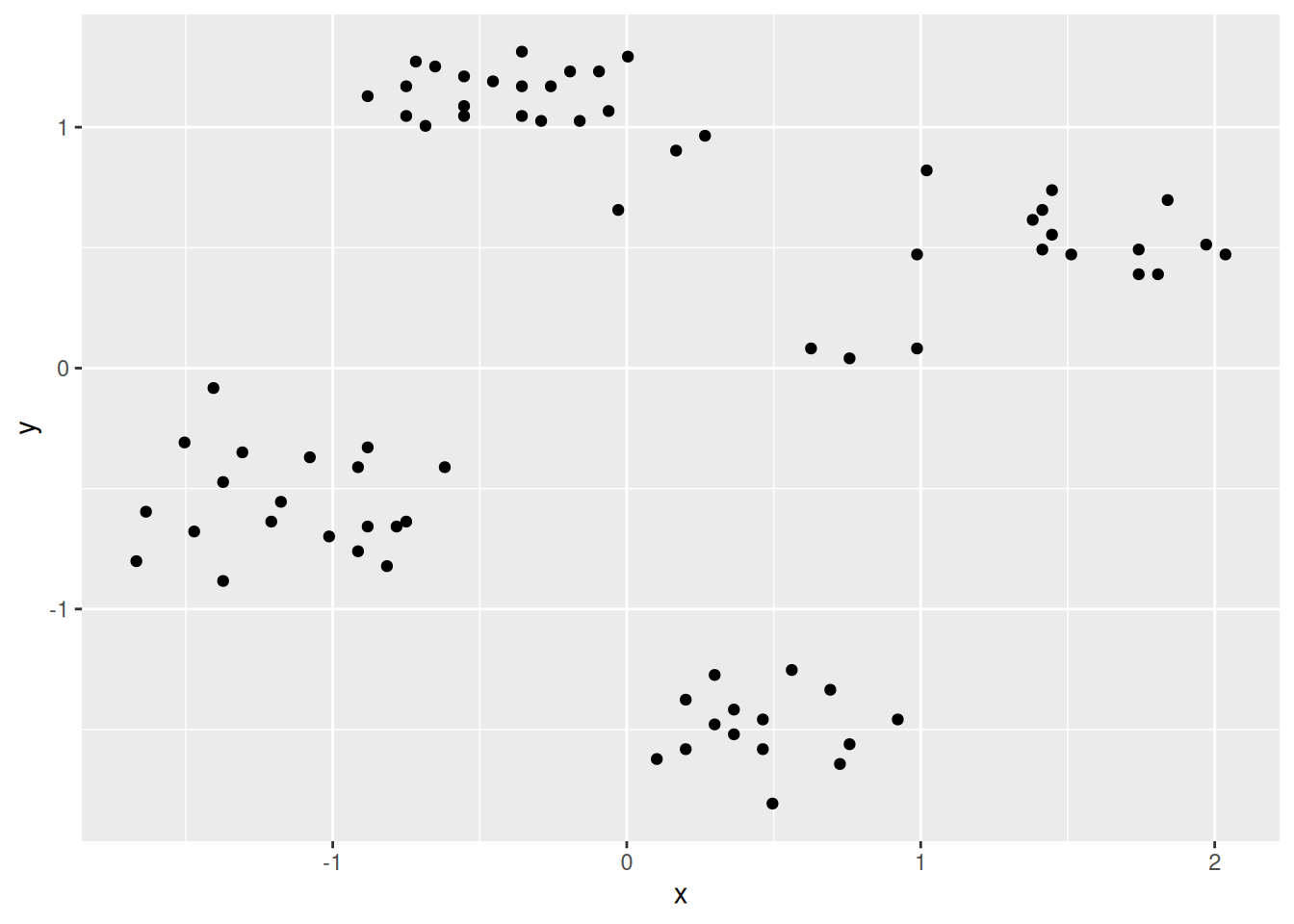
ggplot(shapes, aes(x = x, y = y)) + geom_point()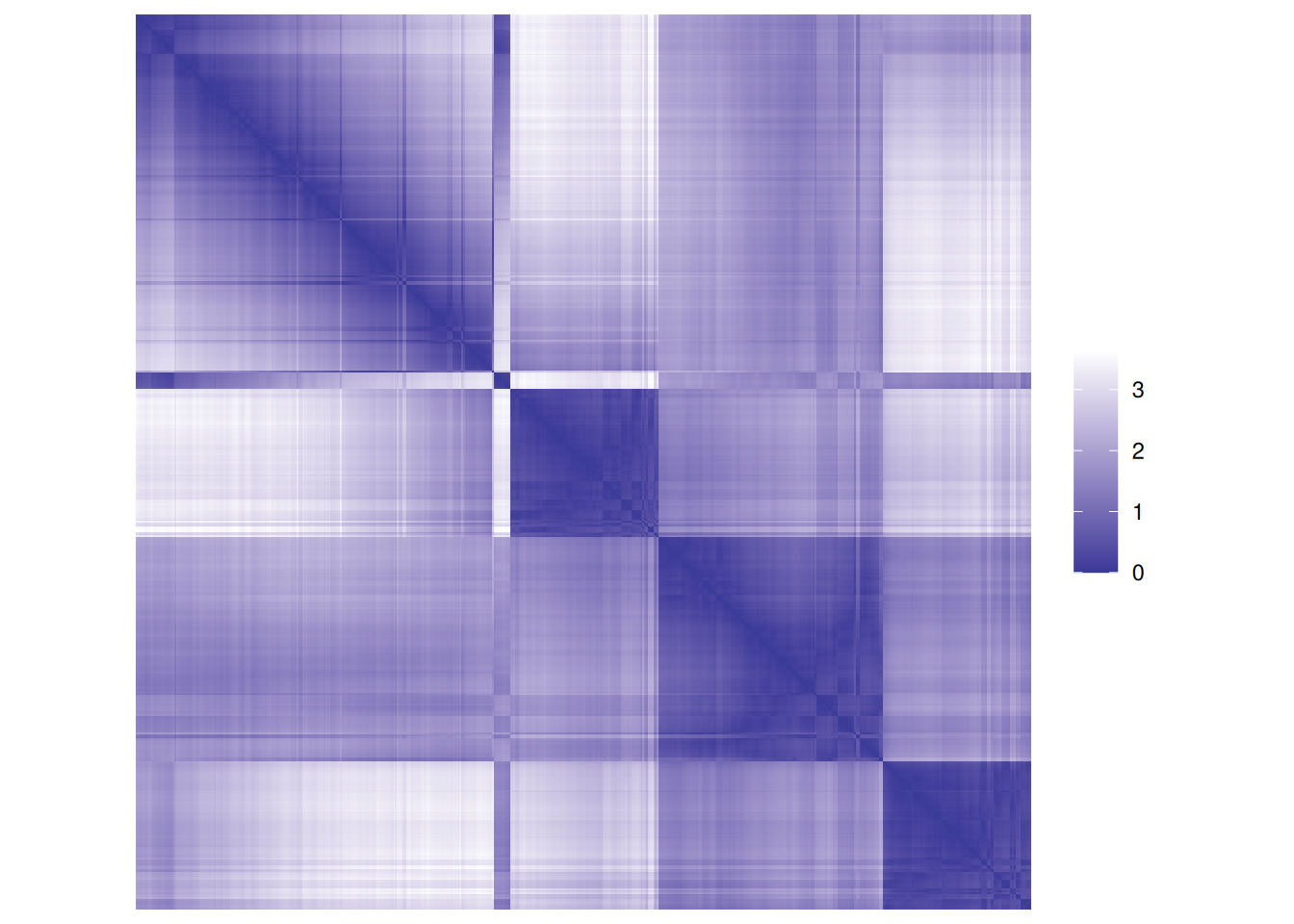

Cluster tendency is typically indicated by several separated point clouds. Often an appropriate number of clusters can also be visually obtained by counting the number of point clouds. We see four clusters, but the mouth is not convex/spherical and thus will pose a problems to algorithms like k-means.

If the data has more than two features then you can use a pairs plot (scatterplot matrix) or look at a scatterplot of the first two principal components using PCA.

7.6.2.2 Visual Analysis for Cluster Tendency Assessment (VAT)

VAT reorders the objects to show potential clustering tendency as a block structure (dark blocks along the main diagonal). We scale the data before using Euclidean distance.

library(seriation)

d_shapes <- dist(scale(shapes))
VAT(d_shapes, col = bluered(100))

iVAT uses the largest distances for all possible paths between two objects instead of the direct distances to make the block structure better visible.

iVAT(d_shapes, col = bluered(100))

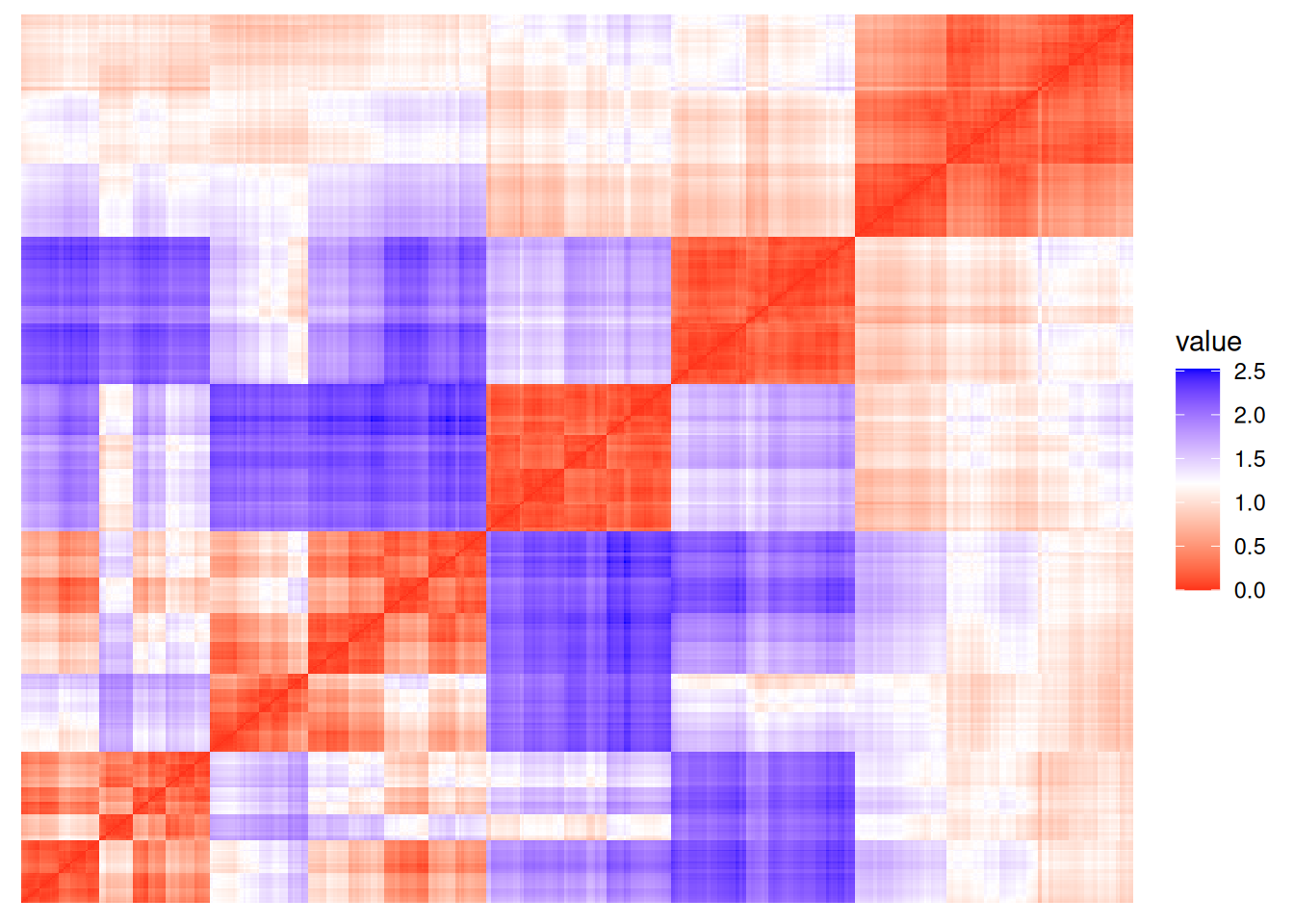
7.6.2.3 Hopkins statistic

factoextra can also create a VAT plot and calculate the Hopkins statistic to assess clustering tendency. For the Hopkins statistic, a sample of size $n$ is drawn from the data and then compares the nearest neighbor distribution with a simulated dataset drawn from a random uniform distribution (see detailed explanation). A values >.5 indicates usually a clustering tendency.

get_clust_tendency(shapes, n = 10)

## $hopkins_stat
## [1] 0.907
## 
## $plot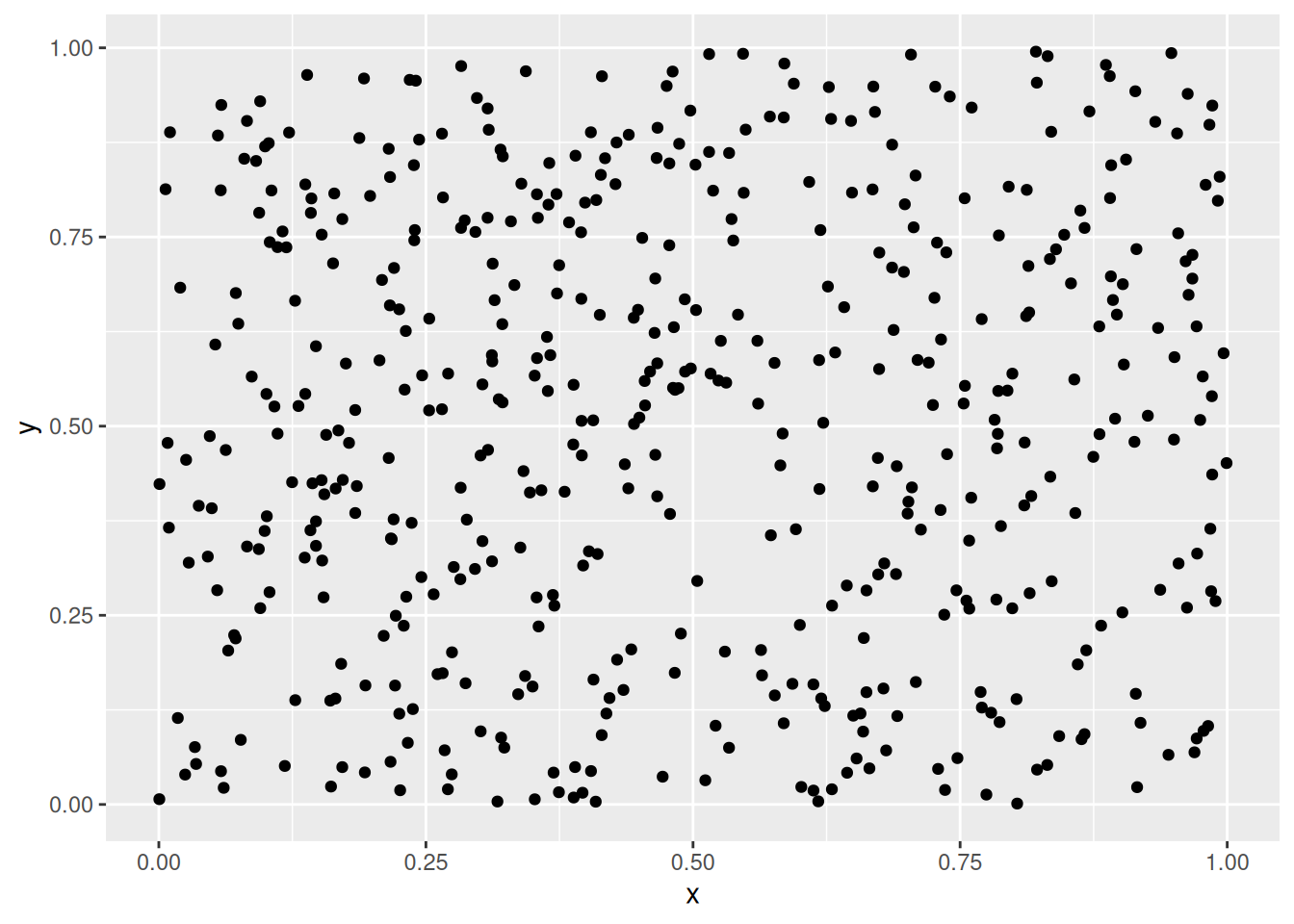

Both plots show a strong cluster structure with 4 clusters.

7.6.2.4 Data Without Clustering Tendency

data_random <- tibble(x = runif(500), y = runif(500))
ggplot(data_random, aes(x, y)) + geom_point()

No point clouds are visible, just noise.

d_random <- dist(data_random)
VAT(d_random, col = bluered(100))

iVAT(d_random, col = bluered(100))

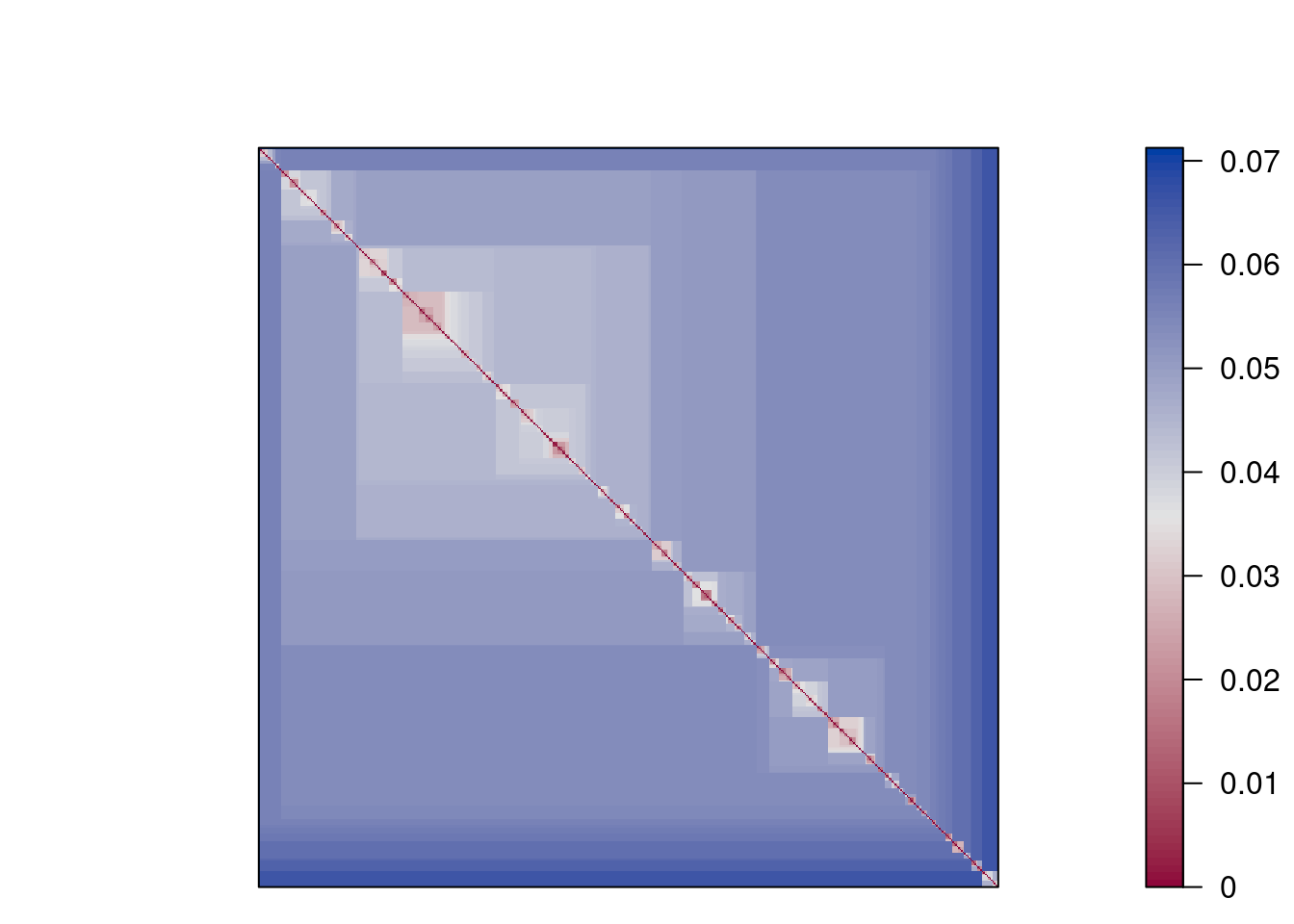
get_clust_tendency(data_random, n = 10, graph = FALSE)

## $hopkins_stat
## [1] 0.464
## 
## $plot
## NULL

There is very little clustering structure visible indicating low clustering tendency and clustering should not be performed on this data. However, k-means can be used to partition the data into $k$ regions of roughly equivalent size. This can be used as a data-driven discretization of the space.

7.6.2.5 k-means on Data Without Clustering Tendency

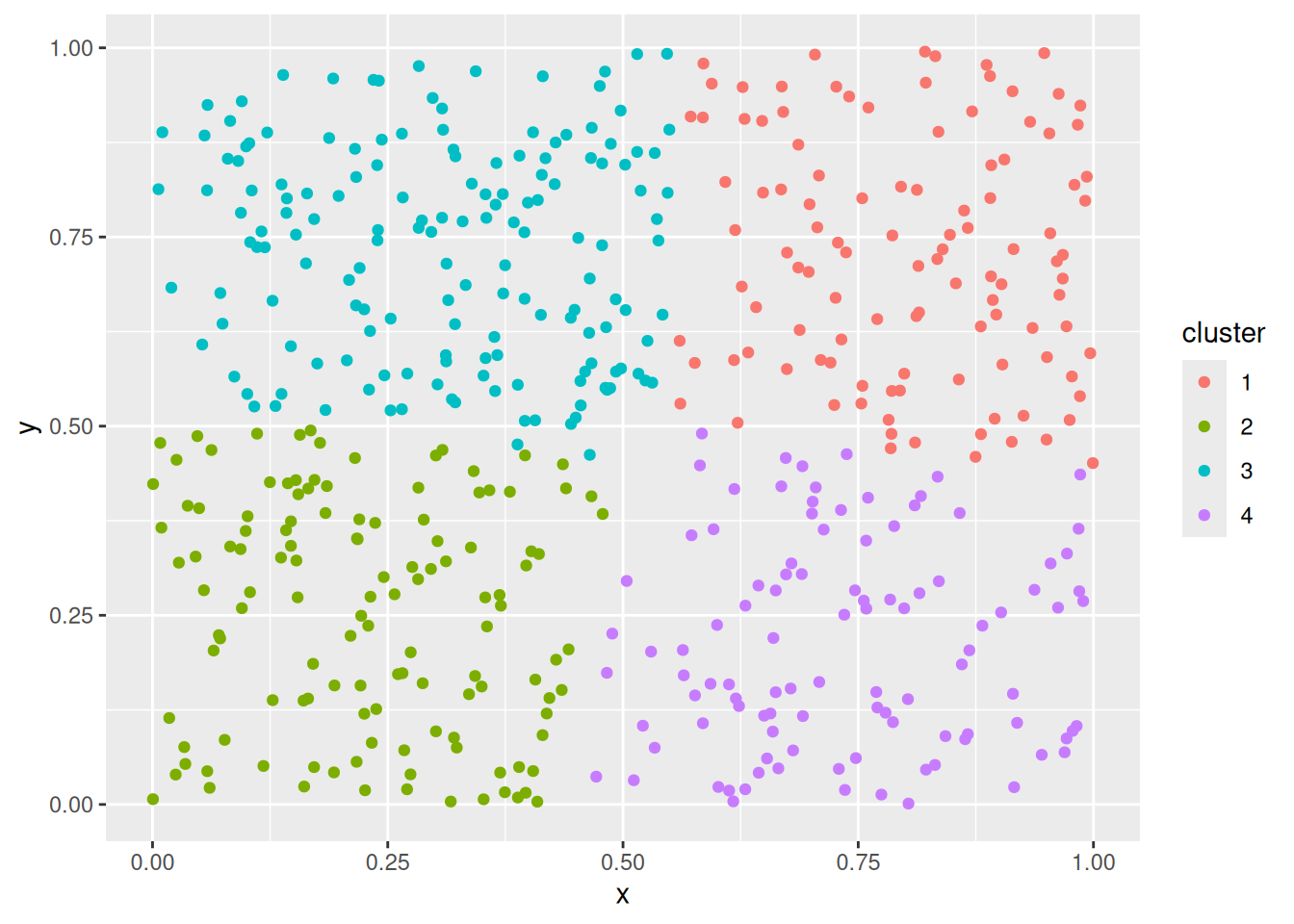
What happens if we perform k-means on data that has no inherent clustering structure?

km <- kmeans(data_random, centers = 4)
random_clustered<- data_random |> add_column(cluster = factor(km$cluster))
ggplot(random_clustered, aes(x = x, y = y, color = cluster)) + geom_point()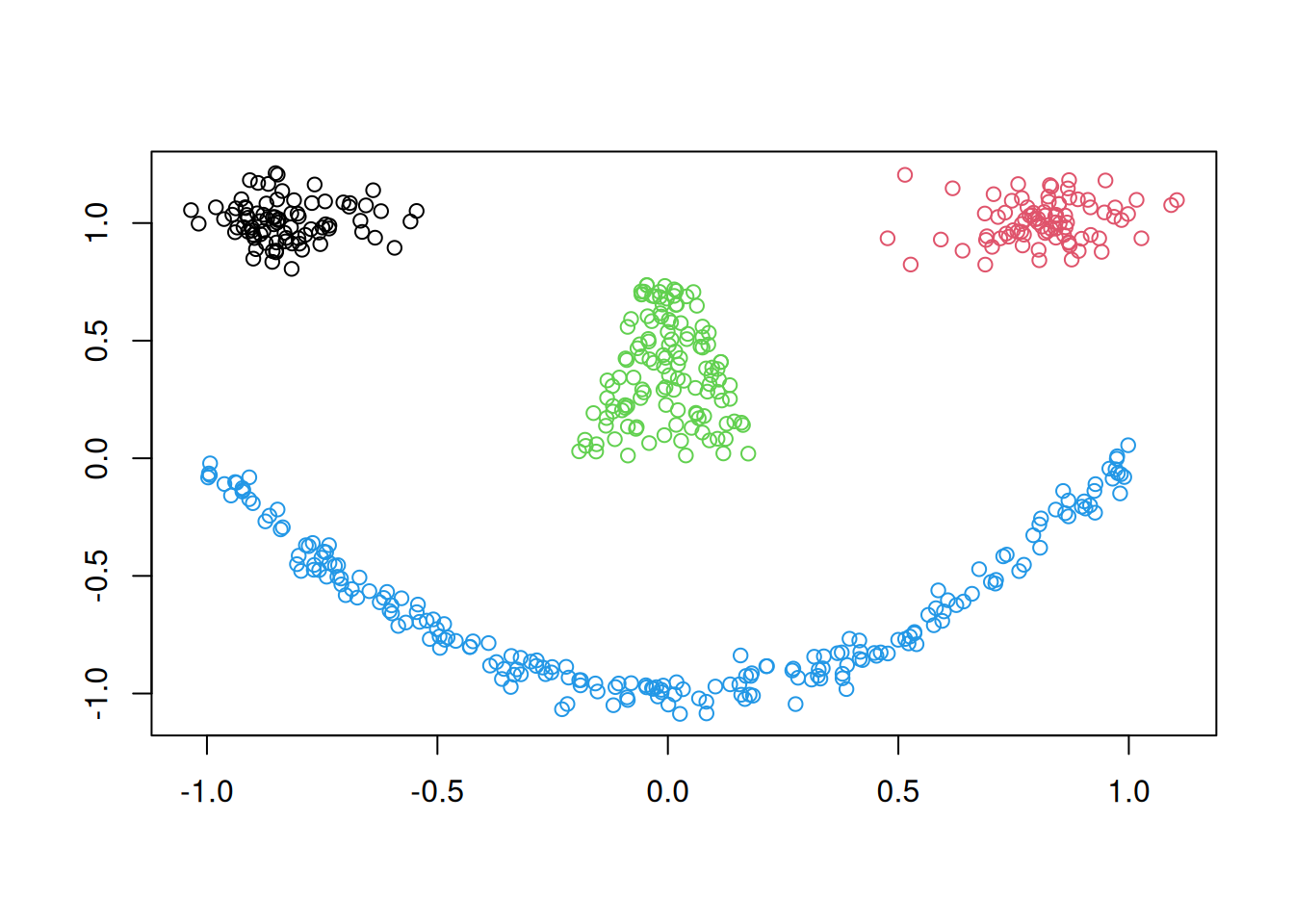

k-means discretizes the space into similarly sized regions.

6 Association Analysis: Advanced Concepts

References