4 Classification: Alternative Techniques
This chapter introduces different types of classifiers. It also discusses the important problem of class imbalance in data and options to deal with it. In addition, this chapter compares visually the decision boundaries used by different algorithms. This will provide a better understanding of the model bias that different algorithms have.
Packages Used in this Chapter
pkgs <- c("basemodels", "C50", "caret", "e1071", "klaR",
"lattice", "MASS", "mlbench", "nnet", "palmerpenguins",
"randomForest", "rpart", "RWeka", "scales", "tidyverse",
"xgboost", "sampling")
pkgs_install <- pkgs[!(pkgs %in% installed.packages()[,"Package"])]
if(length(pkgs_install)) install.packages(pkgs_install)The packages used for this chapter are:
- basemodels (Y.-J. Chen et al. 2023)
- C50 (Kuhn and Quinlan 2025)
- caret (Kuhn 2024)
- e1071 (Meyer et al. 2024)
- klaR (Roever et al. 2023)
- lattice (Sarkar 2025)
- MASS (Ripley and Venables 2025)
- mlbench (Leisch and Dimitriadou 2024)
- nnet (Ripley 2025)
- palmerpenguins (Horst, Hill, and Gorman 2022)
- randomForest (Breiman et al. 2024)
- rpart (Therneau and Atkinson 2025)
- RWeka (Hornik 2023)
- sampling (Tillé and Matei 2025)
- scales (Wickham, Pedersen, and Seidel 2025)
- tidyverse (Wickham 2023b)
- xgboost (T. Chen et al. 2025)
4.1 Types of Classifiers
Many different classification algorithms have been proposed in the literature. In this chapter, we will apply some of the more popular methods.
4.1.1 Set up the Training and Test Data
We will use the Zoo dataset which is included in the R package mlbench
(you may have to install it). The Zoo dataset containing 17 (mostly
logical) variables on different 101 animals as a data frame with 17
columns (hair, feathers, eggs, milk, airborne, aquatic, predator,
toothed, backbone, breathes, venomous, fins, legs, tail, domestic,
catsize, type). We convert the data frame into a tidyverse tibble
(optional).
library(tidyverse)
data(Zoo, package = "mlbench")
Zoo <- as_tibble(Zoo)
Zoo
## # A tibble: 101 × 17
## hair feathers eggs milk airborne aquatic predator
## <lgl> <lgl> <lgl> <lgl> <lgl> <lgl> <lgl>
## 1 TRUE FALSE FALSE TRUE FALSE FALSE TRUE
## 2 TRUE FALSE FALSE TRUE FALSE FALSE FALSE
## 3 FALSE FALSE TRUE FALSE FALSE TRUE TRUE
## 4 TRUE FALSE FALSE TRUE FALSE FALSE TRUE
## 5 TRUE FALSE FALSE TRUE FALSE FALSE TRUE
## 6 TRUE FALSE FALSE TRUE FALSE FALSE FALSE
## 7 TRUE FALSE FALSE TRUE FALSE FALSE FALSE
## 8 FALSE FALSE TRUE FALSE FALSE TRUE FALSE
## 9 FALSE FALSE TRUE FALSE FALSE TRUE TRUE
## 10 TRUE FALSE FALSE TRUE FALSE FALSE FALSE
## # ℹ 91 more rows
## # ℹ 10 more variables: toothed <lgl>, backbone <lgl>,
## # breathes <lgl>, venomous <lgl>, fins <lgl>, legs <int>,
## # tail <lgl>, domestic <lgl>, catsize <lgl>, type <fct>We will use the package caret to make preparing training sets and building classification (and regression) models easier. A great cheat sheet can be found here.
Multi-core support can be used for cross-validation. Note: It is commented out here because it does not work with rJava used by the RWeka-based classifiers below.
##library(doMC, quietly = TRUE)
##registerDoMC(cores = 4)
##getDoParWorkers()Test data is not used in the model building process and needs to be set aside purely for testing the model after it is completely built. Here I use 80% for training.
inTrain <- createDataPartition(y = Zoo$type, p = .8)[[1]]
Zoo_train <- Zoo |> slice(inTrain)
Zoo_test <- Zoo |> slice(-inTrain)For hyperparameter tuning, we will use 10-fold cross-validation.
Note: Be careful if you have many NA values in your data.
train() and cross-validation many fail in some cases. If that is the
case then you can remove features (columns) which have many NAs, omit
NAs using na.omit() or use imputation to replace them with
reasonable values (e.g., by the feature mean or via kNN). Highly
imbalanced datasets are also problematic since there is a chance that a
fold does not contain examples of each class leading to a hard to
understand error message.
4.2 Rule-based classifier: PART
rulesFit <- Zoo_train |> train(type ~ .,
method = "PART",
data = _,
tuneLength = 5,
trControl = trainControl(method = "cv"))
rulesFit
## Rule-Based Classifier
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 74, 74, 74, 74, 75, 75, ...
## Resampling results across tuning parameters:
##
## threshold pruned Accuracy Kappa
## 0.0100 yes 0.9542 0.9382
## 0.0100 no 0.9288 0.9060
## 0.1325 yes 0.9542 0.9382
## 0.1325 no 0.9288 0.9060
## 0.2550 yes 0.9542 0.9382
## 0.2550 no 0.9288 0.9060
## 0.3775 yes 0.9542 0.9382
## 0.3775 no 0.9288 0.9060
## 0.5000 yes 0.9542 0.9382
## 0.5000 no 0.9288 0.9060
##
## Accuracy was used to select the optimal model using
## the largest value.
## The final values used for the model were threshold =
## 0.5 and pruned = yes.The model selection results are shown in the table. This is the selected model:
rulesFit$finalModel
## PART decision list
## ------------------
##
## feathersTRUE <= 0 AND
## milkTRUE > 0: mammal (33.0)
##
## feathersTRUE > 0: bird (16.0)
##
## backboneTRUE <= 0 AND
## airborneTRUE <= 0: mollusc.et.al (9.0/1.0)
##
## airborneTRUE <= 0 AND
## finsTRUE > 0: fish (11.0)
##
## airborneTRUE > 0: insect (6.0)
##
## aquaticTRUE > 0: amphibian (5.0/1.0)
##
## : reptile (3.0)
##
## Number of Rules : 7PART returns a decision list, i.e., an ordered rule set. For example, the first rule shows that an animal with no feathers but milk is a mammal. I ordered rule sets, the decision of the first matching rule is used.
4.3 Nearest Neighbor Classifier
K-Nearest neighbor classifiers classify a new data point by looking at the
majority class labels of its k nearest neighbors in the training data set.
The used kNN implementation uses Euclidean distance to determine what data points
are near by, so data needs be standardized
(scaled) first. Here legs are measured between 0 and 6 while all other
variables are between 0 and 1. Scaling to z-scores can be directly performed as
preprocessing in train using the parameter preProcess = "scale".
The \(k\) value is typically choose as an odd number so we get a clear majority.
knnFit <- Zoo_train |> train(type ~ .,
method = "knn",
data = _,
preProcess = "scale",
tuneGrid = data.frame(k = c(1, 3, 5, 7, 9)),
trControl = trainControl(method = "cv"))
knnFit
## k-Nearest Neighbors
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## Pre-processing: scaled (16)
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 75, 73, 74, 75, 74, 74, ...
## Resampling results across tuning parameters:
##
## k Accuracy Kappa
## 1 0.9428 0.9256
## 3 0.9410 0.9234
## 5 0.9299 0.9088
## 7 0.9031 0.8728
## 9 0.9031 0.8721
##
## Accuracy was used to select the optimal model using
## the largest value.
## The final value used for the model was k = 1.
knnFit$finalModel
## 1-nearest neighbor model
## Training set outcome distribution:
##
## mammal bird reptile fish
## 33 16 4 11
## amphibian insect mollusc.et.al
## 4 7 8kNN classifiers are lazy models meaning that instead of learning, they just keep the complete dataset. This is why the final model just gives us a summary statistic for the class labels in the training data.
4.4 Naive Bayes Classifier
Caret’s train formula interface translates logicals and factors into dummy
variables which the classifier interprets as numbers so it would used a Gaussian naive Bayes estimation. To avoid this, I directly specify x and y.
NBFit <- train(x = as.data.frame(Zoo_train[, -ncol(Zoo_train)]),
y = pull(Zoo_train, "type"),
method = "nb",
tuneGrid = data.frame(fL = c(.2, .5, 1, 5),
usekernel = TRUE, adjust = 1),
trControl = trainControl(method = "cv"))
NBFit
## Naive Bayes
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 74, 75, 74, 76, 74, 75, ...
## Resampling results across tuning parameters:
##
## fL Accuracy Kappa
## 0.2 0.9274 0.9057
## 0.5 0.9274 0.9057
## 1.0 0.9163 0.8904
## 5.0 0.8927 0.8550
##
## Tuning parameter 'usekernel' was held constant at a
## value of TRUE
## Tuning parameter 'adjust' was held
## constant at a value of 1
## Accuracy was used to select the optimal model using
## the largest value.
## The final values used for the model were fL =
## 0.2, usekernel = TRUE and adjust = 1.The final model contains the prior probabilities for each class.
NBFit$finalModel$apriori
## grouping
## mammal bird reptile fish
## 0.39759 0.19277 0.04819 0.13253
## amphibian insect mollusc.et.al
## 0.04819 0.08434 0.09639And the conditional probabilities as a table for each feature. For brevity, we only show the tables for the first three features. For example, the condition probability \(P(\text{hair} = \text{TRUE} | \text{class} = \text{mammal})\) is 0.9641.
NBFit$finalModel$tables[1:3]
## $hair
## var
## grouping FALSE TRUE
## mammal 0.03593 0.96407
## bird 0.98780 0.01220
## reptile 0.95455 0.04545
## fish 0.98246 0.01754
## amphibian 0.95455 0.04545
## insect 0.43243 0.56757
## mollusc.et.al 0.97619 0.02381
##
## $feathers
## var
## grouping FALSE TRUE
## mammal 0.994012 0.005988
## bird 0.012195 0.987805
## reptile 0.954545 0.045455
## fish 0.982456 0.017544
## amphibian 0.954545 0.045455
## insect 0.972973 0.027027
## mollusc.et.al 0.976190 0.023810
##
## $eggs
## var
## grouping FALSE TRUE
## mammal 0.96407 0.03593
## bird 0.01220 0.98780
## reptile 0.27273 0.72727
## fish 0.01754 0.98246
## amphibian 0.04545 0.95455
## insect 0.02703 0.97297
## mollusc.et.al 0.14286 0.857144.5 Bayesian Network
Bayesian networks are not covered here. R has very good support for modeling with Bayesian Networks. An example is the package bnlearn.
4.6 Logistic Regression
Logistic regression is a very powerful classification method and should always be tried as one of the first models. A detailed discussion with more code is available in section Logistic Regression in the Appendix.
Regular logistic regression predicts only one outcome coded as a
binary variable. Since we have data with several
classes, we use multinomial logistic regression,
also called a log-linear model
which is an extension of logistic regresses for multi-class problems.
Caret uses nnet::multinom() which implements penalized multinomial regression.
logRegFit <- Zoo_train |> train(type ~ .,
method = "multinom",
data = _,
trace = FALSE, # suppress some output
trControl = trainControl(method = "cv"))
logRegFit
## Penalized Multinomial Regression
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 75, 76, 75, 74, 74, 74, ...
## Resampling results across tuning parameters:
##
## decay Accuracy Kappa
## 0e+00 0.8704 0.8306
## 1e-04 0.9038 0.8749
## 1e-01 0.9056 0.8777
##
## Accuracy was used to select the optimal model using
## the largest value.
## The final value used for the model was decay = 0.1.
logRegFit$finalModel
## Call:
## nnet::multinom(formula = .outcome ~ ., data = dat, decay = param$decay,
## trace = FALSE)
##
## Coefficients:
## (Intercept) hairTRUE feathersTRUE eggsTRUE
## bird -0.33330 -1.0472 2.9696 0.8278
## reptile 0.01303 -2.0808 -1.0891 0.6731
## fish -0.17462 -0.2762 -0.1135 1.8817
## amphibian -1.28295 -1.5165 -0.2698 0.6801
## insect -0.75300 -0.3903 -0.1445 0.8980
## mollusc.et.al 1.52104 -1.2287 -0.2492 0.9320
## milkTRUE airborneTRUE aquaticTRUE
## bird -1.2523 1.17310 -0.1594
## reptile -2.1800 -0.51796 -1.0890
## fish -1.3571 -0.09009 0.5093
## amphibian -1.6014 -0.36649 1.6271
## insect -1.0130 1.37404 -1.0752
## mollusc.et.al -0.9035 -1.17882 0.7160
## predatorTRUE toothedTRUE backboneTRUE
## bird 0.22312 -1.7846 0.4736
## reptile 0.04172 -0.2003 0.8968
## fish -0.33094 0.4118 0.2768
## amphibian -0.13993 0.7399 0.2557
## insect -1.11743 -1.1852 -1.5725
## mollusc.et.al 0.83070 -1.7390 -2.6045
## breathesTRUE venomousTRUE finsTRUE legs
## bird 0.1337 -0.3278 -0.545979 -0.59910
## reptile -0.5039 1.2776 -1.192197 -0.24200
## fish -1.9709 -0.4204 1.472416 -1.15775
## amphibian 0.4594 0.1611 -0.628746 0.09302
## insect 0.1341 -0.2567 -0.002527 0.59118
## mollusc.et.al -0.6287 0.8411 -0.206104 0.12091
## tailTRUE domesticTRUE catsizeTRUE
## bird 0.5947 0.14176 -0.1182
## reptile 1.1863 -0.40893 -0.4305
## fish 0.3226 0.08636 -0.3132
## amphibian -1.3529 -0.40545 -1.3581
## insect -1.6908 -0.24924 -1.0416
## mollusc.et.al -0.7353 -0.22601 -0.7079
##
## Residual Deviance: 35.46
## AIC: 239.5The coefficients are log odds ratios
measured against the default class (here mammal).
A negative log odds ratio means that the odds go down with an increase in
the value of the predictor. A predictor with a
positive log-odds ratio increases the odds. For example,
in the model above, hair=TRUE has a negative coefficient for
bird but feathers=TRUE has a large positive coefficient.
4.7 Artificial Neural Network (ANN)
Standard networks have an input layer, an output layer and in between a single hidden layer.
nnetFit <- Zoo_train |> train(type ~ .,
method = "nnet",
data = _,
tuneLength = 5,
trControl = trainControl(method = "cv"),
trace = FALSE # no progress output
)
nnetFit
## Neural Network
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 75, 74, 76, 76, 75, 74, ...
## Resampling results across tuning parameters:
##
## size decay Accuracy Kappa
## 1 0e+00 0.7536 0.6369
## 1 1e-04 0.6551 0.4869
## 1 1e-03 0.8201 0.7562
## 1 1e-02 0.7979 0.7285
## 1 1e-01 0.7263 0.6265
## 3 0e+00 0.8344 0.7726
## 3 1e-04 0.8219 0.7622
## 3 1e-03 0.8798 0.8420
## 3 1e-02 0.9063 0.8752
## 3 1e-01 0.8809 0.8405
## 5 0e+00 0.8319 0.7768
## 5 1e-04 0.8448 0.7922
## 5 1e-03 0.9020 0.8660
## 5 1e-02 0.9131 0.8816
## 5 1e-01 0.9020 0.8680
## 7 0e+00 0.8405 0.7893
## 7 1e-04 0.9031 0.8689
## 7 1e-03 0.9020 0.8678
## 7 1e-02 0.9131 0.8816
## 7 1e-01 0.8909 0.8539
## 9 0e+00 0.9145 0.8847
## 9 1e-04 0.9131 0.8804
## 9 1e-03 0.9242 0.8974
## 9 1e-02 0.9131 0.8818
## 9 1e-01 0.9020 0.8680
##
## Accuracy was used to select the optimal model using
## the largest value.
## The final values used for the model were size = 9 and
## decay = 0.001.The input layer has a size of 16, one for each input feature and the output layer has a size of 7 representing the 7 classes. Model selection chose a network architecture with a hidden layer with 9 units resulting in 223 learned weights. Since the model is considered a black-box model only the network architecture and the used variables are shown as a summary.
nnetFit$finalModel
## a 16-9-7 network with 223 weights
## inputs: hairTRUE feathersTRUE eggsTRUE milkTRUE airborneTRUE aquaticTRUE predatorTRUE toothedTRUE backboneTRUE breathesTRUE venomousTRUE finsTRUE legs tailTRUE domesticTRUE catsizeTRUE
## output(s): .outcome
## options were - softmax modelling decay=0.001For deep Learning, R offers packages for using tensorflow and Keras.
4.8 Support Vector Machines
svmFit <- Zoo_train |> train(type ~.,
method = "svmLinear",
data = _,
tuneLength = 5,
trControl = trainControl(method = "cv"))
svmFit
## Support Vector Machines with Linear Kernel
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 77, 75, 74, 76, 75, 74, ...
## Resampling results:
##
## Accuracy Kappa
## 0.9317 0.9105
##
## Tuning parameter 'C' was held constant at a value of 1We use a linear support vector machine.
Support vector machines can use kernels to create non-linear decision boundaries.
method above can be changed to "svmPoly" or "svmRadial" to
use kernels. The choice of kernel is typically make by experimentation.
The support vectors determining the decision boundary are stored in the model.
svmFit$finalModel
## Support Vector Machine object of class "ksvm"
##
## SV type: C-svc (classification)
## parameter : cost C = 1
##
## Linear (vanilla) kernel function.
##
## Number of Support Vectors : 42
##
## Objective Function Value : -0.1432 -0.22 -0.1501 -0.1756 -0.0943 -0.1047 -0.2804 -0.0808 -0.1544 -0.0902 -0.1138 -0.1727 -0.5886 -0.1303 -0.1847 -0.1161 -0.0472 -0.0803 -0.125 -0.15 -0.5704
## Training error : 04.9 Ensemble Methods
Many ensemble methods are available in R. We only cover here code for two popular methods.
4.9.1 Random Forest
randomForestFit <- Zoo_train |> train(type ~ .,
method = "rf",
data = _,
tuneLength = 5,
trControl = trainControl(method = "cv"))
randomForestFit
## Random Forest
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 73, 72, 76, 75, 73, 77, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 2 0.9287 0.9054
## 5 0.9432 0.9246
## 9 0.9398 0.9197
## 12 0.9498 0.9331
## 16 0.9498 0.9331
##
## Accuracy was used to select the optimal model using
## the largest value.
## The final value used for the model was mtry = 12.The default number of trees is 500 and
mtry determines the number of variables randomly sampled as candidates
at each split. This number is a tradeoff where a larger number allows each tree
to pick better splits, but a smaller
number increases the independence between trees.
randomForestFit$finalModel
##
## Call:
## randomForest(x = x, y = y, mtry = param$mtry)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 12
##
## OOB estimate of error rate: 6.02%
## Confusion matrix:
## mammal bird reptile fish amphibian insect
## mammal 33 0 0 0 0 0
## bird 0 16 0 0 0 0
## reptile 0 0 3 0 1 0
## fish 0 0 0 11 0 0
## amphibian 0 0 1 0 3 0
## insect 0 0 0 0 0 6
## mollusc.et.al 0 0 0 0 0 2
## mollusc.et.al class.error
## mammal 0 0.0000
## bird 0 0.0000
## reptile 0 0.2500
## fish 0 0.0000
## amphibian 0 0.2500
## insect 1 0.1429
## mollusc.et.al 6 0.2500The model is a set of 500 trees and the prediction is made by applying all trees and then using the majority vote.
Since random forests use bagging (bootstrap sampling to train trees), the remaining data can be used like a test set. The resulting error is called out-of-bag (OOB) error and gives an estimate for the generalization error. The model above also shows the confusion matrix based on the OOB error.
4.9.2 Gradient Boosted Decision Trees (xgboost)
The idea of gradient boosting is to learn a base model and then to learn successive models to predict and correct the error of all previous models. Typically, tree models are used.
xgboostFit <- Zoo_train |> train(type ~ .,
method = "xgbTree",
data = _,
tuneLength = 5,
trControl = trainControl(method = "cv"),
tuneGrid = expand.grid(
nrounds = 20,
max_depth = 3,
colsample_bytree = .6,
eta = 0.1,
gamma=0,
min_child_weight = 1,
subsample = .5
))
xgboostFit
## eXtreme Gradient Boosting
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 74, 74, 76, 73, 76, 74, ...
## Resampling results:
##
## Accuracy Kappa
## 0.92 0.893
##
## Tuning parameter 'nrounds' was held constant at a value
## held constant at a value of 1
## Tuning parameter
## 'subsample' was held constant at a value of 0.5The final model is a complicated set of trees, so only some summary information is shown.
xgboostFit$finalModel
## ##### xgb.Booster
## raw: 111.6 Kb
## call:
## xgboost::xgb.train(params = list(eta = param$eta, max_depth = param$max_depth,
## gamma = param$gamma, colsample_bytree = param$colsample_bytree,
## min_child_weight = param$min_child_weight, subsample = param$subsample),
## data = x, nrounds = param$nrounds, num_class = length(lev),
## objective = "multi:softprob")
## params (as set within xgb.train):
## eta = "0.1", max_depth = "3", gamma = "0", colsample_bytree = "0.6", min_child_weight = "1", subsample = "0.5", num_class = "7", objective = "multi:softprob", validate_parameters = "TRUE"
## xgb.attributes:
## niter
## callbacks:
## cb.print.evaluation(period = print_every_n)
## # of features: 16
## niter: 20
## nfeatures : 16
## xNames : hairTRUE feathersTRUE eggsTRUE milkTRUE airborneTRUE aquaticTRUE predatorTRUE toothedTRUE backboneTRUE breathesTRUE venomousTRUE finsTRUE legs tailTRUE domesticTRUE catsizeTRUE
## problemType : Classification
## tuneValue :
## nrounds max_depth eta gamma colsample_bytree
## 1 20 3 0.1 0 0.6
## min_child_weight subsample
## 1 1 0.5
## obsLevels : mammal bird reptile fish amphibian insect mollusc.et.al
## param :
## list()4.10 Model Comparison
We first create a weak baseline model that always predicts the the majority class mammal.
baselineFit <- Zoo_train |> train(type ~ .,
method = basemodels::dummyClassifier,
data = _,
strategy = "constant",
constant = "mammal",
trControl = trainControl(method = "cv"
))
baselineFit
## dummyClassifier
##
## 83 samples
## 16 predictors
## 7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 76, 75, 75, 74, 76, 76, ...
## Resampling results:
##
## Accuracy Kappa
## 0.4025 0The kappa of 0 clearly indicates that the baseline model has no power.
We collect the performance metrics from the models trained on the same data.
resamps <- resamples(list(
baseline = baselineFit,
PART = rulesFit,
kNearestNeighbors = knnFit,
NBayes = NBFit,
logReg = logRegFit,
ANN = nnetFit,
SVM = svmFit,
RandomForest = randomForestFit,
XGBoost = xgboostFit
))
resamps
##
## Call:
## resamples.default(x = list(baseline = baselineFit, PART
## svmFit, RandomForest = randomForestFit, XGBoost
## = xgboostFit))
##
## Models: baseline, PART, kNearestNeighbors, NBayes, logReg, ANN, SVM, RandomForest, XGBoost
## Number of resamples: 10
## Performance metrics: Accuracy, Kappa
## Time estimates for: everything, final model fitThe summary statistics shows the performance. We see that all methods do well on this easy data set, only the baseline model performs as expected poorly.
summary(resamps)
##
## Call:
## summary.resamples(object = resamps)
##
## Models: baseline, PART, kNearestNeighbors, NBayes, logReg, ANN, SVM, RandomForest, XGBoost
## Number of resamples: 10
##
## Accuracy
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## baseline 0.3000 0.3750 0.4286 0.4025 0.4405 0.5
## PART 0.8750 0.8889 1.0000 0.9542 1.0000 1.0
## kNearestNeighbors 0.8750 0.8889 0.9500 0.9428 1.0000 1.0
## NBayes 0.7778 0.8750 0.9444 0.9274 1.0000 1.0
## logReg 0.7500 0.8056 0.9444 0.9056 1.0000 1.0
## ANN 0.8571 0.8750 0.8889 0.9242 1.0000 1.0
## SVM 0.7778 0.8785 0.9500 0.9317 1.0000 1.0
## RandomForest 0.8571 0.8835 1.0000 0.9498 1.0000 1.0
## XGBoost 0.7778 0.8472 0.9500 0.9200 1.0000 1.0
## NA's
## baseline 0
## PART 0
## kNearestNeighbors 0
## NBayes 0
## logReg 0
## ANN 0
## SVM 0
## RandomForest 0
## XGBoost 0
##
## Kappa
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## baseline 0.0000 0.0000 0.0000 0.0000 0 0
## PART 0.8222 0.8542 1.0000 0.9382 1 1
## kNearestNeighbors 0.8333 0.8588 0.9324 0.9256 1 1
## NBayes 0.7353 0.8220 0.9297 0.9057 1 1
## logReg 0.6596 0.7560 0.9308 0.8777 1 1
## ANN 0.7879 0.8241 0.8615 0.8974 1 1
## SVM 0.7273 0.8413 0.9342 0.9105 1 1
## RandomForest 0.8000 0.8483 1.0000 0.9331 1 1
## XGBoost 0.7000 0.7848 0.9367 0.8930 1 1
## NA's
## baseline 0
## PART 0
## kNearestNeighbors 0
## NBayes 0
## logReg 0
## ANN 0
## SVM 0
## RandomForest 0
## XGBoost 0
library(lattice)
bwplot(resamps, layout = c(3, 1))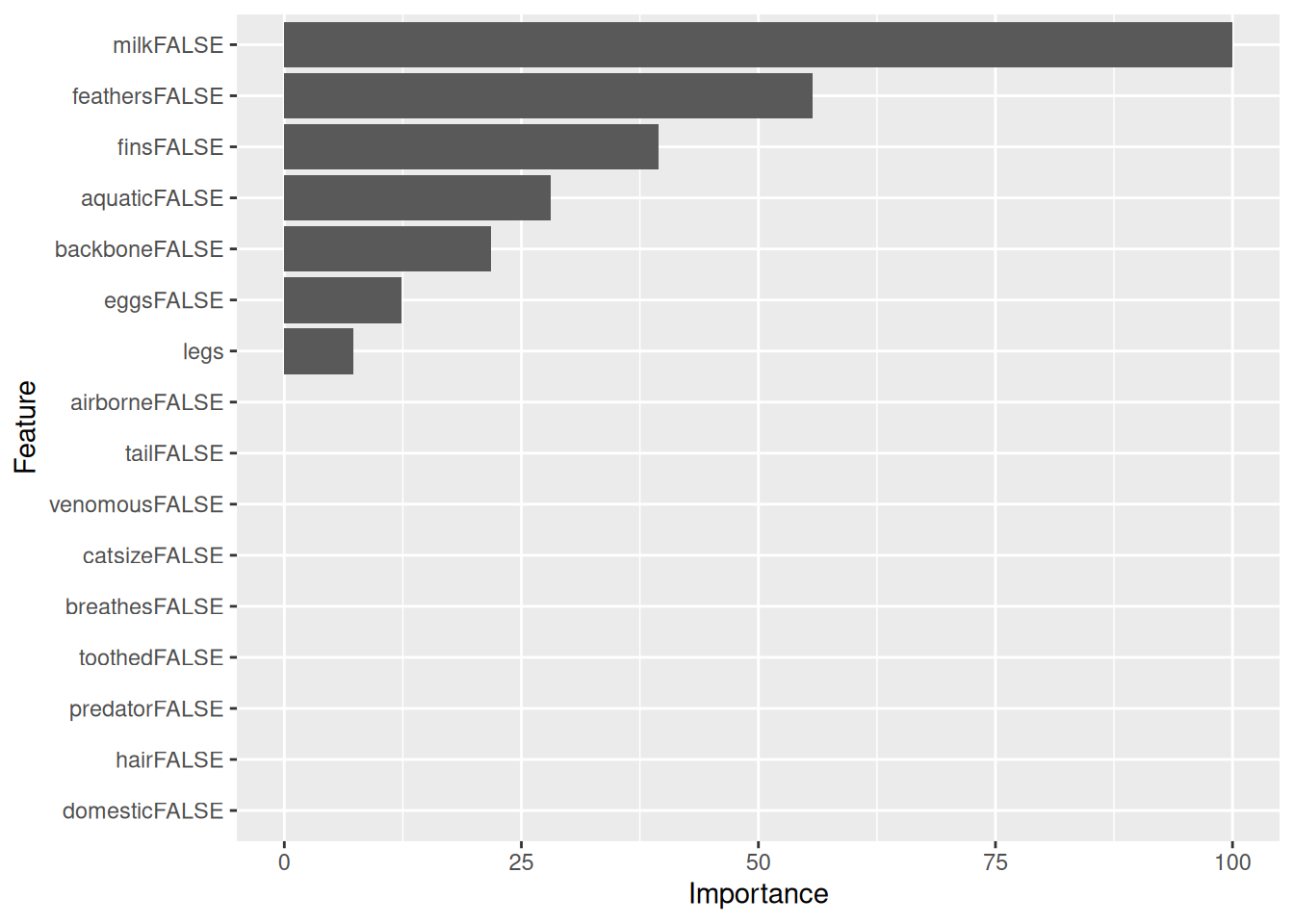
Perform inference about differences between models. For each metric, all pair-wise differences are computed and tested to assess if the difference is equal to zero. By default Bonferroni correction for multiple comparison is used. Differences are shown in the upper triangle and p-values are in the lower triangle.
difs <- diff(resamps)
summary(difs)
##
## Call:
## summary.diff.resamples(object = difs)
##
## p-value adjustment: bonferroni
## Upper diagonal: estimates of the difference
## Lower diagonal: p-value for H0: difference = 0
##
## Accuracy
## baseline PART kNearestNeighbors
## baseline -0.55171 -0.54032
## PART 8.37e-07 0.01139
## kNearestNeighbors 3.20e-07 1
## NBayes 7.48e-06 1 1
## logReg 1.81e-05 1 1
## ANN 9.66e-06 1 1
## SVM 2.87e-06 1 1
## RandomForest 9.73e-07 1 1
## XGBoost 2.04e-05 1 1
## NBayes logReg ANN SVM
## baseline -0.52492 -0.50310 -0.52175 -0.52921
## PART 0.02679 0.04861 0.02996 0.02250
## kNearestNeighbors 0.01540 0.03722 0.01857 0.01111
## NBayes 0.02183 0.00317 -0.00429
## logReg 1 -0.01865 -0.02611
## ANN 1 1 -0.00746
## SVM 1 1 1
## RandomForest 1 1 1 1
## XGBoost 1 1 1 1
## RandomForest XGBoost
## baseline -0.54738 -0.51754
## PART 0.00433 0.03417
## kNearestNeighbors -0.00706 0.02278
## NBayes -0.02246 0.00738
## logReg -0.04428 -0.01444
## ANN -0.02563 0.00421
## SVM -0.01817 0.01167
## RandomForest 0.02984
## XGBoost 1
##
## Kappa
## baseline PART kNearestNeighbors
## baseline -0.93815 -0.92557
## PART 1.41e-09 0.01258
## kNearestNeighbors 1.37e-09 1
## NBayes 1.94e-08 1 1
## logReg 4.17e-07 1 1
## ANN 6.28e-09 1 1
## SVM 1.45e-08 1 1
## RandomForest 3.67e-09 1 1
## XGBoost 1.03e-07 1 1
## NBayes logReg ANN SVM
## baseline -0.90570 -0.87768 -0.89737 -0.91054
## PART 0.03245 0.06047 0.04078 0.02761
## kNearestNeighbors 0.01987 0.04789 0.02820 0.01503
## NBayes 0.02802 0.00833 -0.00485
## logReg 1 -0.01969 -0.03287
## ANN 1 1 -0.01317
## SVM 1 1 1
## RandomForest 1 1 1 1
## XGBoost 1 1 1 1
## RandomForest XGBoost
## baseline -0.93305 -0.89296
## PART 0.00510 0.04519
## kNearestNeighbors -0.00748 0.03261
## NBayes -0.02735 0.01274
## logReg -0.05538 -0.01529
## ANN -0.03568 0.00441
## SVM -0.02251 0.01758
## RandomForest 0.04009
## XGBoost 1All perform similarly well except the baseline model (differences in the first row are negative and the p-values in the first column are <.05 indicating that the null-hypothesis of a difference of 0 can be rejected). Most models do similarly well on the data. We choose here the random forest model and evaluate its generalization performance on the held-out test set.
pr <- predict(randomForestFit, Zoo_test)
pr
## [1] mammal fish mollusc.et.al fish
## [5] mammal insect mammal mammal
## [9] mammal mammal bird mammal
## [13] mammal bird reptile bird
## [17] mollusc.et.al bird
## 7 Levels: mammal bird reptile fish amphibian ... mollusc.et.alCalculate the confusion matrix for the held-out test data.
confusionMatrix(pr, reference = Zoo_test$type)
## Confusion Matrix and Statistics
##
## Reference
## Prediction mammal bird reptile fish amphibian insect
## mammal 8 0 0 0 0 0
## bird 0 4 0 0 0 0
## reptile 0 0 1 0 0 0
## fish 0 0 0 2 0 0
## amphibian 0 0 0 0 0 0
## insect 0 0 0 0 0 1
## mollusc.et.al 0 0 0 0 0 0
## Reference
## Prediction mollusc.et.al
## mammal 0
## bird 0
## reptile 0
## fish 0
## amphibian 0
## insect 0
## mollusc.et.al 2
##
## Overall Statistics
##
## Accuracy : 1
## 95% CI : (0.815, 1)
## No Information Rate : 0.444
## P-Value [Acc > NIR] : 4.58e-07
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: mammal Class: bird
## Sensitivity 1.000 1.000
## Specificity 1.000 1.000
## Pos Pred Value 1.000 1.000
## Neg Pred Value 1.000 1.000
## Prevalence 0.444 0.222
## Detection Rate 0.444 0.222
## Detection Prevalence 0.444 0.222
## Balanced Accuracy 1.000 1.000
## Class: reptile Class: fish
## Sensitivity 1.0000 1.000
## Specificity 1.0000 1.000
## Pos Pred Value 1.0000 1.000
## Neg Pred Value 1.0000 1.000
## Prevalence 0.0556 0.111
## Detection Rate 0.0556 0.111
## Detection Prevalence 0.0556 0.111
## Balanced Accuracy 1.0000 1.000
## Class: amphibian Class: insect
## Sensitivity NA 1.0000
## Specificity 1 1.0000
## Pos Pred Value NA 1.0000
## Neg Pred Value NA 1.0000
## Prevalence 0 0.0556
## Detection Rate 0 0.0556
## Detection Prevalence 0 0.0556
## Balanced Accuracy NA 1.0000
## Class: mollusc.et.al
## Sensitivity 1.000
## Specificity 1.000
## Pos Pred Value 1.000
## Neg Pred Value 1.000
## Prevalence 0.111
## Detection Rate 0.111
## Detection Prevalence 0.111
## Balanced Accuracy 1.0004.11 Class Imbalance
Classifiers have a hard time to learn from data where we have much more observations for one class (called the majority class). This is called the class imbalance problem which is especially problematic when it is important to identify members of the minority class. In this setting the minority class is also often called the positive class since it has the property that we want to identify. An example would be that we want to identify the patients that are positive for a rare disease.
Here is a very good article about the problem and solutions.
For the examples, we will use the Zoo dataset.
library(rpart)
library(rpart.plot)
data(Zoo, package = "mlbench")You always need to check if you have a class imbalance problem. Just look at the class distribution.
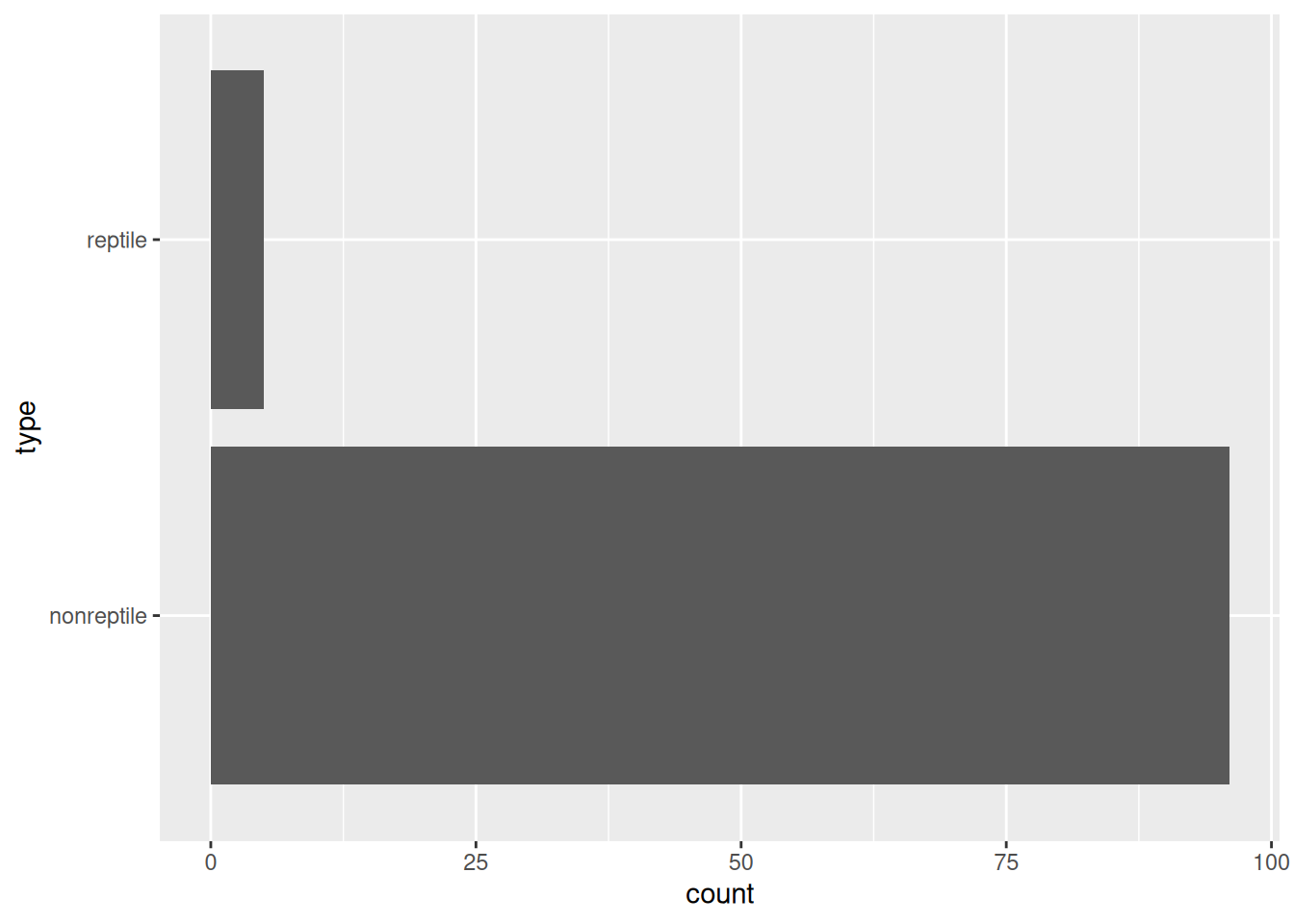
We see that there is moderate class imbalance with very many mammals and few amphibians and reptiles in the data set. If we build a classifier, then it is very likely that it will not perform well for identifying amphibians or reptiles. This effect was seen when building a simple decision tree.
tree_default <- Zoo |>
rpart(type ~ ., data = _)
tree_default
## n= 101
##
## node), split, n, loss, yval, (yprob)
## * denotes terminal node
##
## 1) root 101 60 mammal (0.41 0.2 0.05 0.13 0.04 0.079 0.099)
## 2) milk>=0.5 41 0 mammal (1 0 0 0 0 0 0) *
## 3) milk< 0.5 60 40 bird (0 0.33 0.083 0.22 0.067 0.13 0.17)
## 6) feathers>=0.5 20 0 bird (0 1 0 0 0 0 0) *
## 7) feathers< 0.5 40 27 fish (0 0 0.12 0.33 0.1 0.2 0.25)
## 14) fins>=0.5 13 0 fish (0 0 0 1 0 0 0) *
## 15) fins< 0.5 27 17 mollusc.et.al (0 0 0.19 0 0.15 0.3 0.37)
## 30) backbone>=0.5 9 4 reptile (0 0 0.56 0 0.44 0 0) *
## 31) backbone< 0.5 18 8 mollusc.et.al (0 0 0 0 0 0.44 0.56) *
library(rpart.plot)
rpart.plot(tree_default, extra = 2)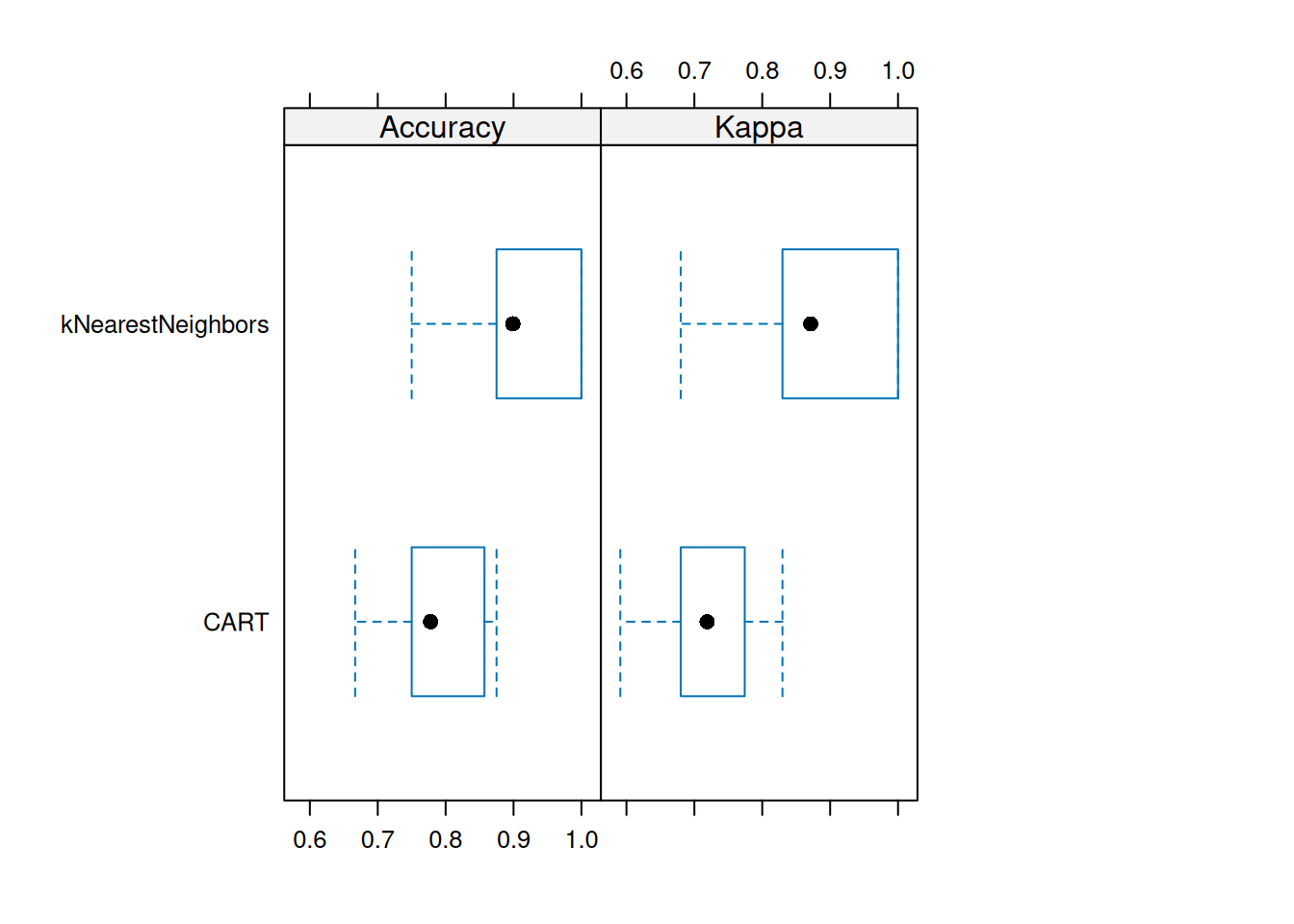
The resulting tree has no leaf nodes for these rare animal types meaning that it cannot identify them.
Deciding if an animal is a reptile or not is a very class imbalanced problem. We set up this problem by changing the class variable to make it into a binary reptile/non-reptile classification problem.
Zoo_reptile <- Zoo |>
mutate(type = factor(Zoo$type == "reptile",
levels = c(FALSE, TRUE),
labels = c("nonreptile", "reptile")))Do not forget to make the class variable a factor (a nominal variable) or you will get a regression tree instead of a classification tree.
By checking the class distribution, we see that classification model is now highly imbalances with only 5 reptiles vs. 96 non-reptiles.
summary(Zoo_reptile)
## hair feathers eggs
## Mode :logical Mode :logical Mode :logical
## FALSE:58 FALSE:81 FALSE:42
## TRUE :43 TRUE :20 TRUE :59
##
##
##
## milk airborne aquatic
## Mode :logical Mode :logical Mode :logical
## FALSE:60 FALSE:77 FALSE:65
## TRUE :41 TRUE :24 TRUE :36
##
##
##
## predator toothed backbone
## Mode :logical Mode :logical Mode :logical
## FALSE:45 FALSE:40 FALSE:18
## TRUE :56 TRUE :61 TRUE :83
##
##
##
## breathes venomous fins
## Mode :logical Mode :logical Mode :logical
## FALSE:21 FALSE:93 FALSE:84
## TRUE :80 TRUE :8 TRUE :17
##
##
##
## legs tail domestic
## Min. :0.00 Mode :logical Mode :logical
## 1st Qu.:2.00 FALSE:26 FALSE:88
## Median :4.00 TRUE :75 TRUE :13
## Mean :2.84
## 3rd Qu.:4.00
## Max. :8.00
## catsize type
## Mode :logical nonreptile:96
## FALSE:57 reptile : 5
## TRUE :44
##
##
## 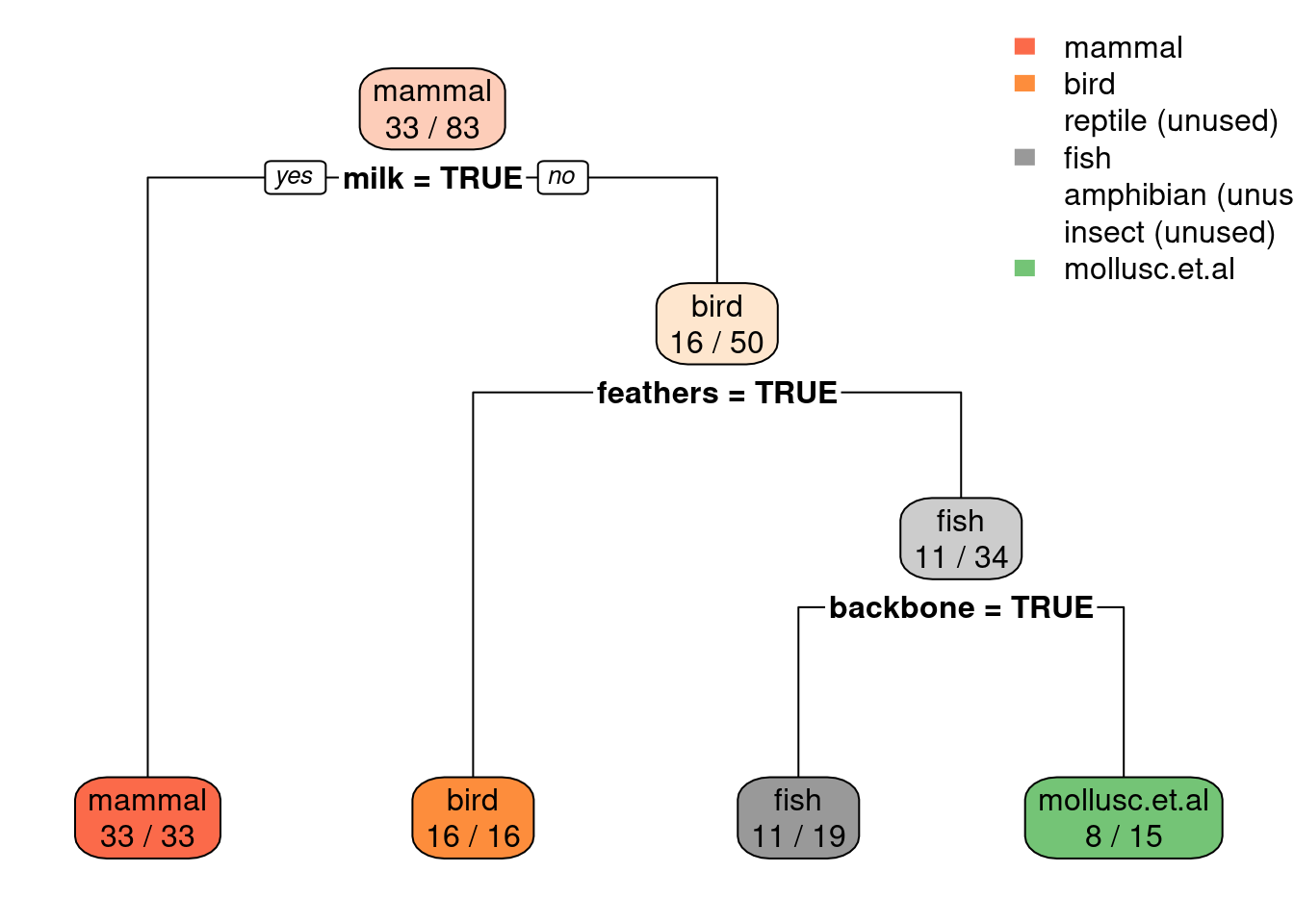
The graph shows that the data is highly imbalanced with encountering a non-reptile being about 20 times more likely then encountering a reptile. We will try several different options in the next few subsections.
We split the data into test and training data so we can evaluate how well the classifiers for the different options work. I use here a 50/50 split to make sure that the test set has some samples of the rare reptile class.
set.seed(1234)
inTrain <- createDataPartition(y = Zoo_reptile$type, p = .5)[[1]]
training_reptile <- Zoo_reptile |> slice(inTrain)
testing_reptile <- Zoo_reptile |> slice(-inTrain)4.11.1 Option 1: Use the Data As Is and Hope For The Best
fit <- training_reptile |>
train(type ~ .,
data = _,
method = "rpart",
trControl = trainControl(method = "cv"))
## Warning in nominalTrainWorkflow(x = x, y = y, wts =
## weights, info = trainInfo, : There were missing values in
## resampled performance measures.Warnings: “There were missing values in resampled performance measures.” means that some test folds used in hyper parameter tuning did not contain examples of both classes. This is very likely with strong class imbalance and small datasets.
fit
## CART
##
## 51 samples
## 16 predictors
## 2 classes: 'nonreptile', 'reptile'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 46, 47, 46, 46, 45, 46, ...
## Resampling results:
##
## Accuracy Kappa
## 0.9467 0
##
## Tuning parameter 'cp' was held constant at a value of 0
rpart.plot(fit$finalModel, extra = 2)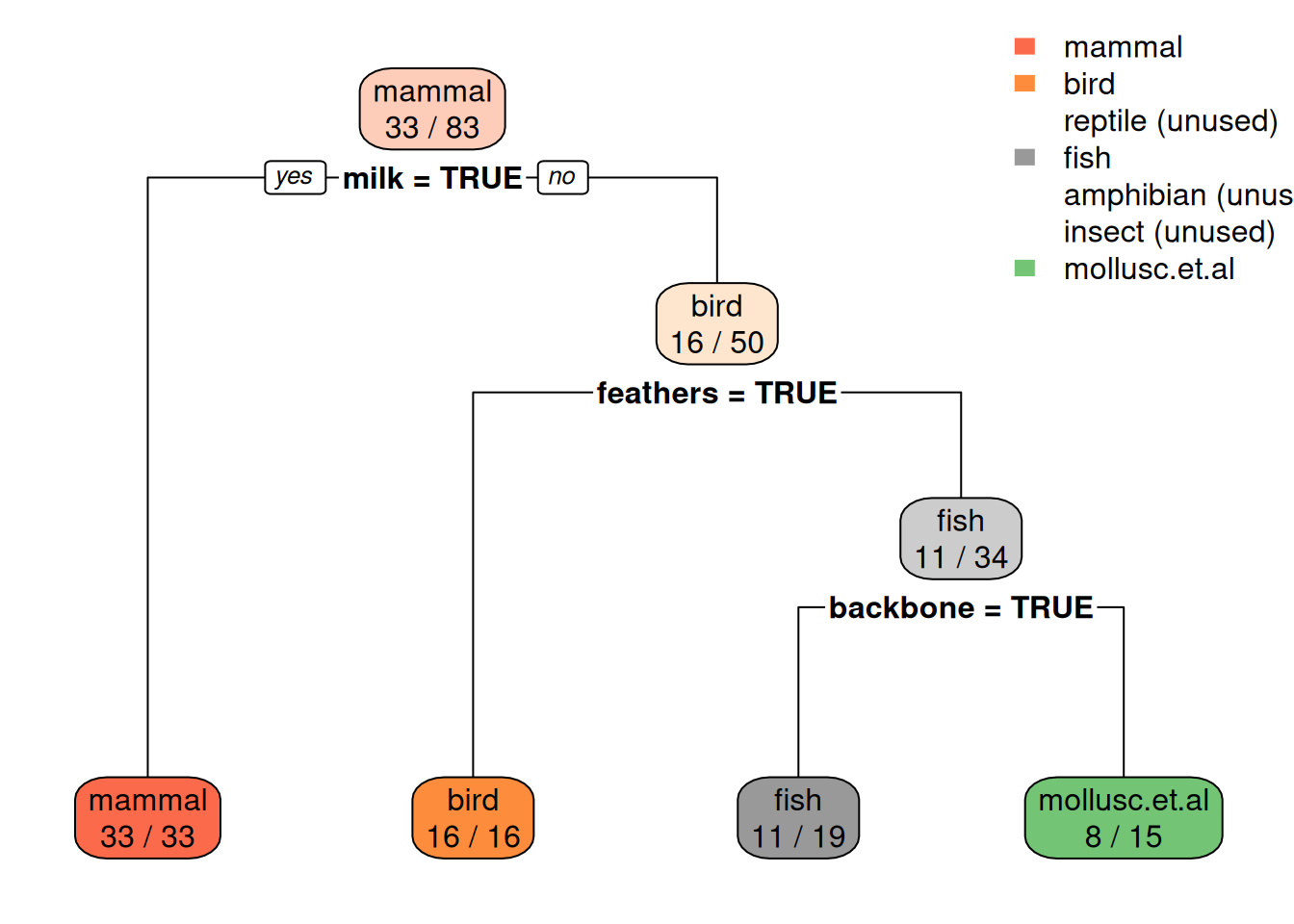
The tree predicts everything as non-reptile. Have a look at the error on the test set.
confusionMatrix(data = predict(fit, testing_reptile),
ref = testing_reptile$type, positive = "reptile")
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonreptile reptile
## nonreptile 48 2
## reptile 0 0
##
## Accuracy : 0.96
## 95% CI : (0.863, 0.995)
## No Information Rate : 0.96
## P-Value [Acc > NIR] : 0.677
##
## Kappa : 0
##
## Mcnemar's Test P-Value : 0.480
##
## Sensitivity : 0.00
## Specificity : 1.00
## Pos Pred Value : NaN
## Neg Pred Value : 0.96
## Prevalence : 0.04
## Detection Rate : 0.00
## Detection Prevalence : 0.00
## Balanced Accuracy : 0.50
##
## 'Positive' Class : reptile
## Accuracy is high, but it is exactly the same as the no-information rate and kappa is zero. Sensitivity is also zero, meaning that we do not identify any positive (reptile). If the cost of missing a positive is much larger than the cost associated with misclassifying a negative, then accuracy is not a good measure! By dealing with imbalance, we are not concerned with accuracy, but we want to increase the sensitivity, i.e., the chance to identify positive examples. This approach does not work!
Note: The positive class value (the one that you want to detect) is
set manually to reptile using positive = "reptile". Otherwise
sensitivity/specificity will not be correctly calculated.
4.11.2 Option 2: Balance Data With Resampling
A popular choice is to balance the class distribution by using stratified sampling with replacement to oversample the minority/positive class. Other options include SMOTE (in package DMwR) or other sampling strategies (e.g., from package unbalanced).
Here, we use stratified sampling with 50 observations per class. Note: many samples of the positive/minority class will be chosen several times.
library(sampling)
##
## Attaching package: 'sampling'
## The following object is masked from 'package:caret':
##
## cluster
set.seed(1000) # for repeatability
id <- strata(training_reptile, stratanames = "type",
size = c(50, 50), method = "srswr")
training_reptile_balanced <- training_reptile |>
slice(id$ID_unit)
table(training_reptile_balanced$type)
##
## nonreptile reptile
## 50 50Build a tree using the balanced data.
fit <- training_reptile_balanced |>
train(type ~ .,
data = _,
method = "rpart",
trControl = trainControl(method = "cv"),
control = rpart.control(minsplit = 5))
fit
## CART
##
## 100 samples
## 16 predictor
## 2 classes: 'nonreptile', 'reptile'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 90, 90, 90, 90, 90, 90, ...
## Resampling results across tuning parameters:
##
## cp Accuracy Kappa
## 0.18 0.81 0.62
## 0.30 0.63 0.26
## 0.34 0.53 0.06
##
## Accuracy was used to select the optimal model using
## the largest value.
## The final value used for the model was cp = 0.18.
rpart.plot(fit$finalModel, extra = 2)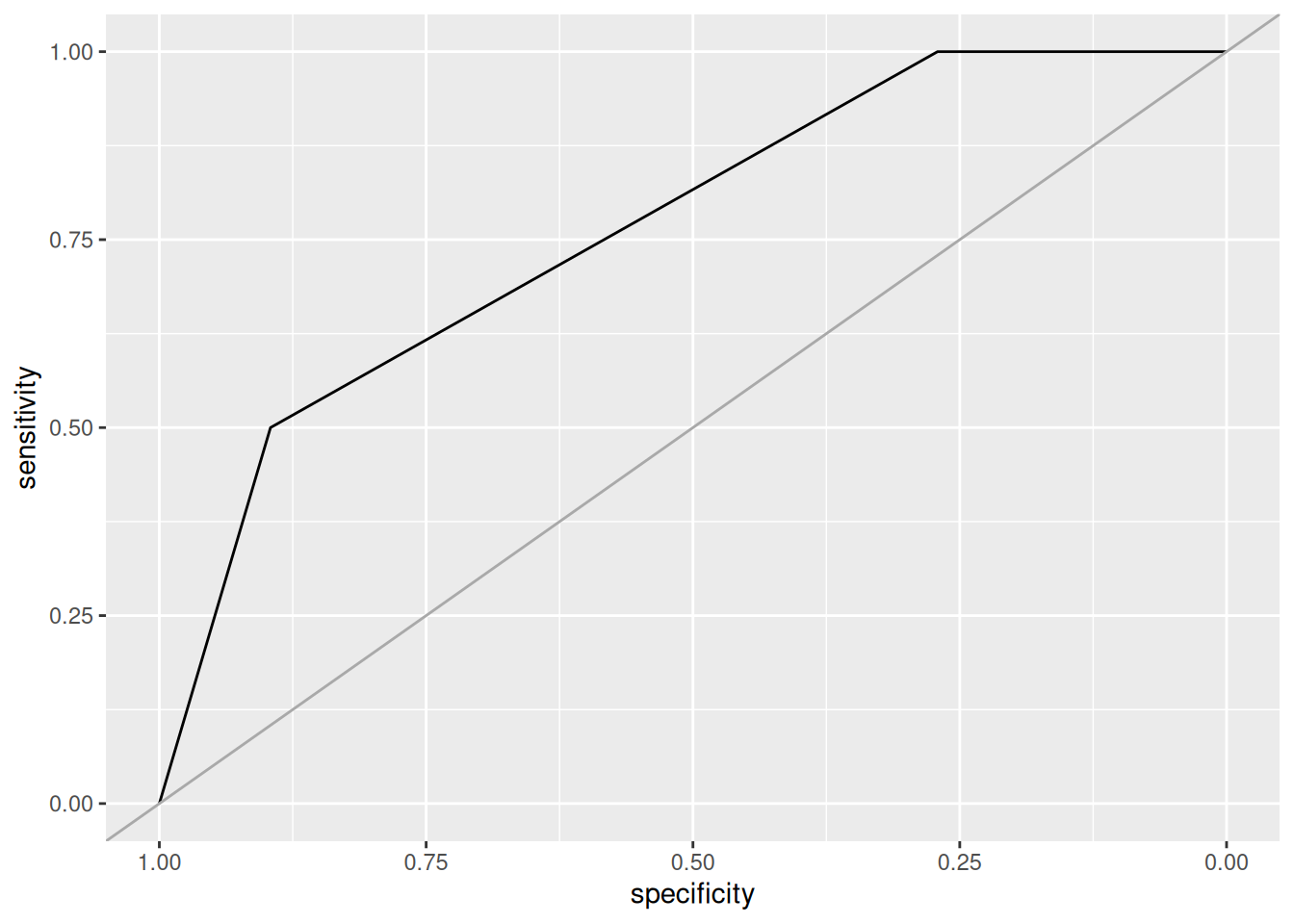
The resulting tree has a reasonable accuracy/kappa on the balanced data.
However, the real data does not have the distribution of the balanced data, so
we check the model on the unbalanced testing data.
confusionMatrix(data = predict(fit, testing_reptile),
ref = testing_reptile$type, positive = "reptile")
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonreptile reptile
## nonreptile 19 0
## reptile 29 2
##
## Accuracy : 0.42
## 95% CI : (0.282, 0.568)
## No Information Rate : 0.96
## P-Value [Acc > NIR] : 1
##
## Kappa : 0.05
##
## Mcnemar's Test P-Value : 2e-07
##
## Sensitivity : 1.0000
## Specificity : 0.3958
## Pos Pred Value : 0.0645
## Neg Pred Value : 1.0000
## Prevalence : 0.0400
## Detection Rate : 0.0400
## Detection Prevalence : 0.6200
## Balanced Accuracy : 0.6979
##
## 'Positive' Class : reptile
## The accuracy is below the no information rate and kappa is close to 0! However, sensitivity (the ability to identify reptiles) is now one meaning that the classifier is able to identify all reptiles.
We have to make a tradeoff between sensitivity (identifying reptiles) and specificity (how many of the identified animals are really reptiles). The tradeoff can be controlled using the sample proportions. We can sample more reptiles to increase sensitivity at the cost of lower specificity (this effect cannot be seen in the data since the test set has only a few reptiles).
id <- strata(training_reptile, stratanames = "type",
size = c(50, 500), method = "srswr")
training_reptile_balanced <- training_reptile |>
slice(id$ID_unit)
table(training_reptile_balanced$type)
##
## nonreptile reptile
## 50 500
fit <- training_reptile_balanced |>
train(type ~ .,
data = _,
method = "rpart",
trControl = trainControl(method = "cv"),
control = rpart.control(minsplit = 5))
confusionMatrix(data = predict(fit, testing_reptile),
ref = testing_reptile$type, positive = "reptile")
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonreptile reptile
## nonreptile 33 0
## reptile 15 2
##
## Accuracy : 0.7
## 95% CI : (0.554, 0.821)
## No Information Rate : 0.96
## P-Value [Acc > NIR] : 1.000000
##
## Kappa : 0.15
##
## Mcnemar's Test P-Value : 0.000301
##
## Sensitivity : 1.000
## Specificity : 0.688
## Pos Pred Value : 0.118
## Neg Pred Value : 1.000
## Prevalence : 0.040
## Detection Rate : 0.040
## Detection Prevalence : 0.340
## Balanced Accuracy : 0.844
##
## 'Positive' Class : reptile
## Note: We have used a sample ratio of 1:10 meaning that we value identifying 1 reptile as much as misscassifying 10 non-reptiles. This is related to the cost usd by the cost-sensitive classifier introduced in Option 4 below.
4.11.3 Option 3: Build A Larger Tree and use Predicted Probabilities
Increase complexity and require less data for splitting a node. Here I also use AUC (area under the ROC) as the tuning metric. You need to specify the two class summary function. Note that the tree still trying to improve accuracy on the data and not AUC! I also enable class probabilities since I want to predict probabilities later.
fit <- training_reptile |>
train(type ~ .,
data = _,
method = "rpart",
tuneLength = 10,
trControl = trainControl(
method = "cv",
classProbs = TRUE, ## for predict with type="prob"
summaryFunction=twoClassSummary), ## for ROC
metric = "ROC",
control = rpart.control(minsplit = 3))
## Warning in nominalTrainWorkflow(x = x, y = y, wts =
## weights, info = trainInfo, : There were missing values in
## resampled performance measures.
fit
## CART
##
## 51 samples
## 16 predictors
## 2 classes: 'nonreptile', 'reptile'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 46, 45, 46, 45, 47, 47, ...
## Resampling results:
##
## ROC Sens Spec
## 0.4333 0.92 0
##
## Tuning parameter 'cp' was held constant at a value of 0
rpart.plot(fit$finalModel, extra = 2)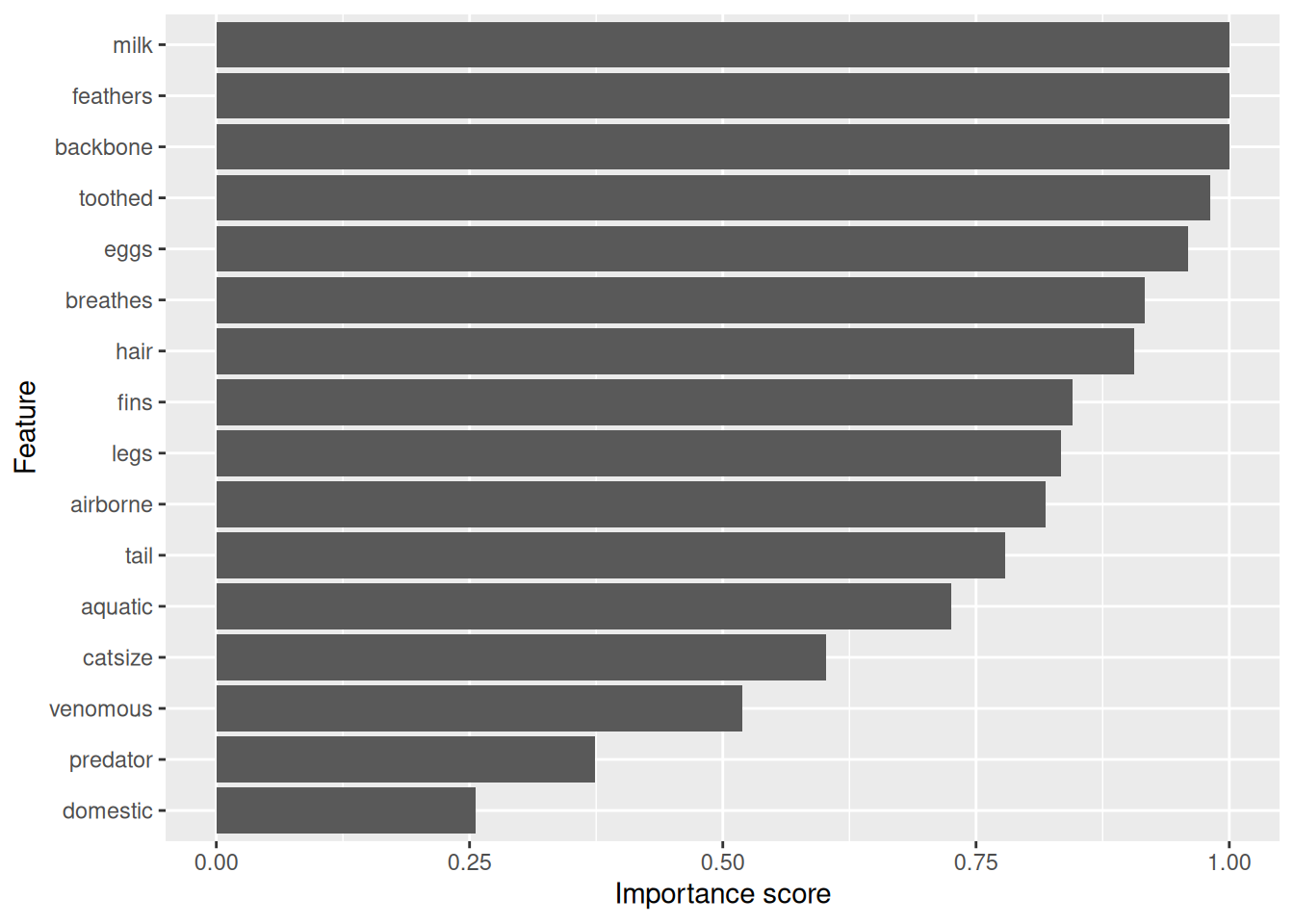
confusionMatrix(data = predict(fit, testing_reptile),
ref = testing_reptile$type, positive = "reptile")
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonreptile reptile
## nonreptile 48 2
## reptile 0 0
##
## Accuracy : 0.96
## 95% CI : (0.863, 0.995)
## No Information Rate : 0.96
## P-Value [Acc > NIR] : 0.677
##
## Kappa : 0
##
## Mcnemar's Test P-Value : 0.480
##
## Sensitivity : 0.00
## Specificity : 1.00
## Pos Pred Value : NaN
## Neg Pred Value : 0.96
## Prevalence : 0.04
## Detection Rate : 0.00
## Detection Prevalence : 0.00
## Balanced Accuracy : 0.50
##
## 'Positive' Class : reptile
## Note: Accuracy is high, but it is close or below to the no-information rate!
4.11.3.1 Create A Biased Classifier
We can create a classifier which will detect more reptiles at the expense of misclassifying non-reptiles. This is equivalent to increasing the cost of misclassifying a reptile as a non-reptile. The usual rule is to predict in each node the majority class from the test data in the node. For a binary classification problem that means a probability of >50%. In the following, we reduce this threshold to 1% or more. This means that if the new observation ends up in a leaf node with 1% or more reptiles from training then the observation will be classified as a reptile. The data set is small and this works better with more data.
prob <- predict(fit, testing_reptile, type = "prob")
tail(prob)
## nonreptile reptile
## tuna 1.0000 0.00000
## vole 0.9615 0.03846
## wasp 0.5000 0.50000
## wolf 0.9615 0.03846
## worm 1.0000 0.00000
## wren 0.9615 0.03846
pred <- ifelse(prob[,"reptile"] >= 0.01, "reptile", "nonreptile") |>
as.factor()
confusionMatrix(data = pred,
ref = testing_reptile$type, positive = "reptile")
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonreptile reptile
## nonreptile 13 0
## reptile 35 2
##
## Accuracy : 0.3
## 95% CI : (0.179, 0.446)
## No Information Rate : 0.96
## P-Value [Acc > NIR] : 1
##
## Kappa : 0.029
##
## Mcnemar's Test P-Value : 9.08e-09
##
## Sensitivity : 1.0000
## Specificity : 0.2708
## Pos Pred Value : 0.0541
## Neg Pred Value : 1.0000
## Prevalence : 0.0400
## Detection Rate : 0.0400
## Detection Prevalence : 0.7400
## Balanced Accuracy : 0.6354
##
## 'Positive' Class : reptile
## Note that accuracy goes down and is below the no information rate. However, both measures are based on the idea that all errors have the same cost. What is important is that we are now able to find more reptiles.
4.11.3.2 Plot the ROC Curve
Since we have a binary classification problem and a classifier that predicts a probability for an observation to be a reptile, we can also use a receiver operating characteristic (ROC) curve. For the ROC curve all different cutoff thresholds for the probability are used and then connected with a line. The area under the curve represents a single number for how well the classifier works (the closer to one, the better).
library("pROC")
## Type 'citation("pROC")' for a citation.
##
## Attaching package: 'pROC'
## The following objects are masked from 'package:stats':
##
## cov, smooth, var
r <- roc(testing_reptile$type == "reptile", prob[,"reptile"])
## Setting levels: control = FALSE, case = TRUE
## Setting direction: controls < cases
r
##
## Call:
## roc.default(response = testing_reptile$type == "reptile", predictor = prob[, "reptile"])
##
## Data: prob[, "reptile"] in 48 controls (testing_reptile$type == "reptile" FALSE) < 2 cases (testing_reptile$type == "reptile" TRUE).
## Area under the curve: 0.766
ggroc(r) + geom_abline(intercept = 1, slope = 1, color = "darkgrey")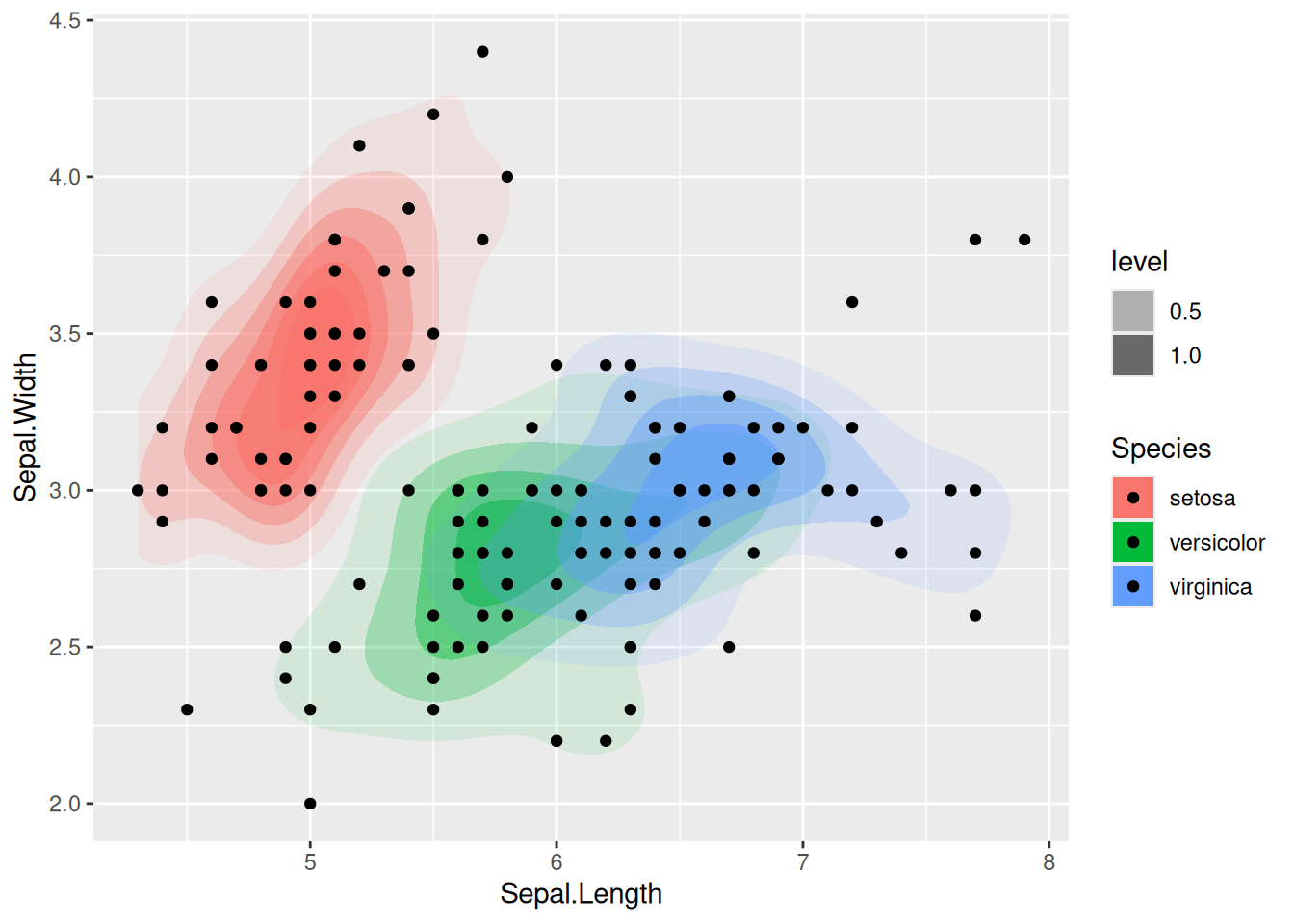
4.11.4 Option 4: Use a Cost-Sensitive Classifier
The implementation of CART in rpart can use a cost matrix for making
splitting decisions (as parameter loss). The matrix has the form
TP FP
FN TNwhere TP and TN have to be 0. We make FN very expensive with a cost of 100 compared to the cost for FP of 1.
cost <- matrix(c(
0, 1,
100, 0
), byrow = TRUE, nrow = 2)
cost
## [,1] [,2]
## [1,] 0 1
## [2,] 100 0
fit <- training_reptile |>
train(type ~ .,
data = _,
method = "rpart",
parms = list(loss = cost),
trControl = trainControl(method = "cv"))
## Warning in nominalTrainWorkflow(x = x, y = y, wts =
## weights, info = trainInfo, : There were missing values in
## resampled performance measures.The warning “There were missing values in resampled performance measures” means that some folds did not contain any reptiles (because of the class imbalance) and thus the performance measures could not be calculates.
fit
## CART
##
## 51 samples
## 16 predictors
## 2 classes: 'nonreptile', 'reptile'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 46, 46, 46, 46, 46, 45, ...
## Resampling results:
##
## Accuracy Kappa
## 0.5417 -0.0409
##
## Tuning parameter 'cp' was held constant at a value of 0
rpart.plot(fit$finalModel, extra = 2)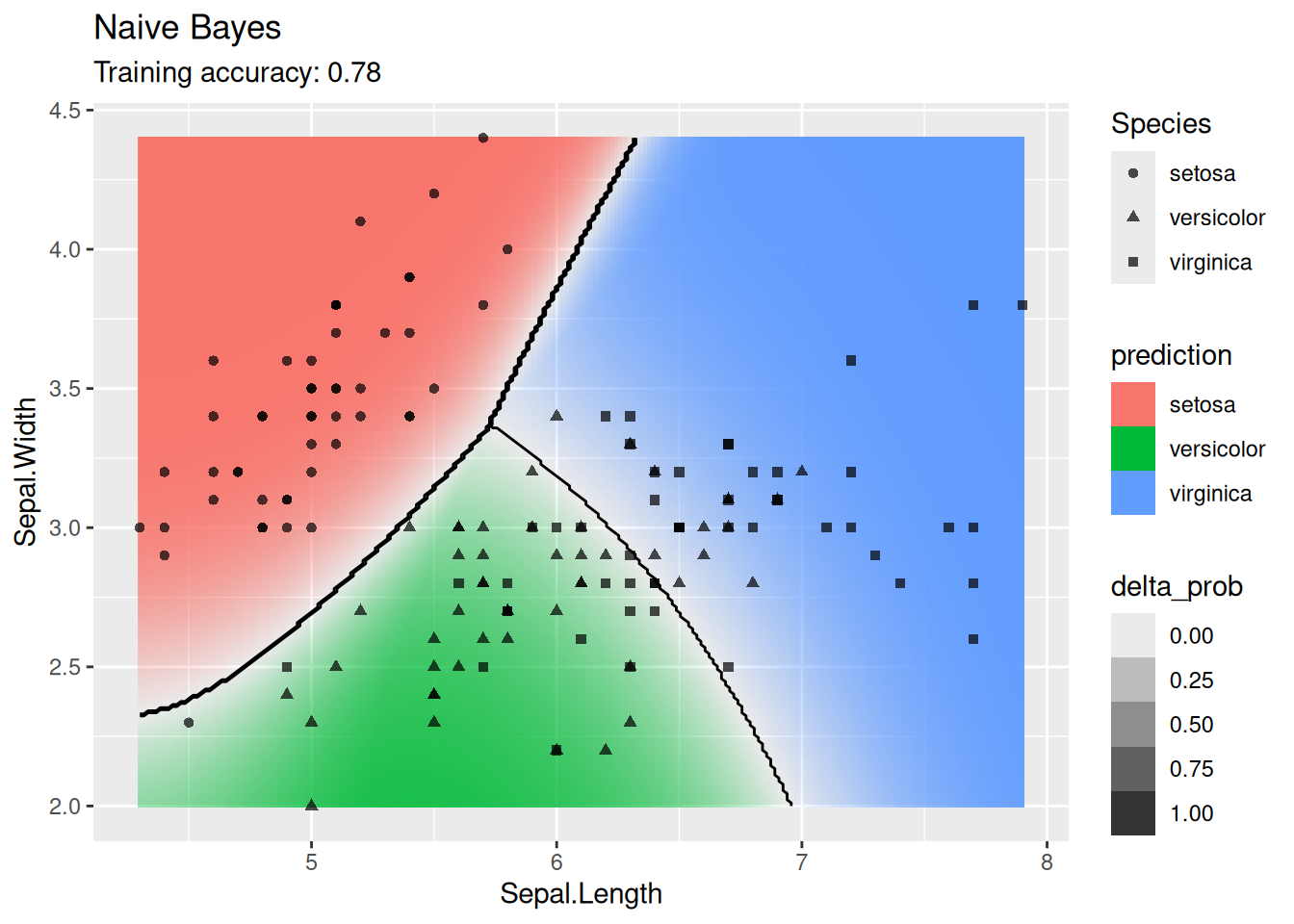
confusionMatrix(data = predict(fit, testing_reptile),
ref = testing_reptile$type, positive = "reptile")
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonreptile reptile
## nonreptile 39 0
## reptile 9 2
##
## Accuracy : 0.82
## 95% CI : (0.686, 0.914)
## No Information Rate : 0.96
## P-Value [Acc > NIR] : 0.99998
##
## Kappa : 0.257
##
## Mcnemar's Test P-Value : 0.00766
##
## Sensitivity : 1.000
## Specificity : 0.812
## Pos Pred Value : 0.182
## Neg Pred Value : 1.000
## Prevalence : 0.040
## Detection Rate : 0.040
## Detection Prevalence : 0.220
## Balanced Accuracy : 0.906
##
## 'Positive' Class : reptile
## The high cost for false negatives results in a classifier that does not miss any reptile.
Note: Using a cost-sensitive classifier is often the best option. Unfortunately, most classification algorithms (or their implementation) do not have the ability to consider misclassification cost. Cost-sensitivity can be added to ANNs by changing the optimized loss function from pure cross-entropy loss to a weighted version. Using a custom loss function is possible in most deep learning libraries.
4.12 Comparing Decision Boundaries of Popular Classification Techniques*
Classifiers create decision boundaries to discriminate between classes. Different classifiers are able to create different shapes of decision boundaries (e.g., some are strictly linear) and thus some classifiers may perform better for certain datasets. In this section, we visualize the decision boundaries found by several popular classification methods.
The following function defines a plot that adds the decision boundary (black lines) and the difference between the classification probability of the two best classes (color intensity; indifference is 0 shown as white) by evaluating the classifier at evenly spaced grid points. Note that low resolution will make evaluation faster but it also will make the decision boundary look like it has small steps even if it is a straight line.
decisionplot <- function(model, data, class_var,
predict_type = c("class", "prob"), resolution = 3 * 72) {
# resolution is set to 72 dpi for 3 inches wide images.
y <- data |> pull(class_var)
x <- data |> dplyr::select(-all_of(class_var))
# resubstitution accuracy
prediction <- predict(model, x, type = predict_type[1])
# LDA returns a list
if(is.list(prediction)) prediction <- prediction$class
prediction <- factor(prediction, levels = levels(y))
cm <- confusionMatrix(data = prediction,
reference = y)
acc <- cm$overall["Accuracy"]
# evaluate model on a grid
r <- sapply(x[, 1:2], range, na.rm = TRUE)
xs <- seq(r[1,1], r[2,1], length.out = resolution)
ys <- seq(r[1,2], r[2,2], length.out = resolution)
g <- cbind(rep(xs, each = resolution), rep(ys,
time = resolution))
colnames(g) <- colnames(r)
g <- as_tibble(g)
# guess how to get class labels from predict
# (unfortunately not very consistent between models)
cl <- predict(model, g, type = predict_type[1])
prob <- NULL
if(is.list(cl)) { # LDA returns a list
prob <- cl$posterior
cl <- cl$class
} else if (inherits(model, "svm"))
prob <- attr(predict(model, g, probability = TRUE), "probabilities")
else
if(!is.na(predict_type[2]))
try(prob <- predict(model, g, type = predict_type[2]))
# We visualize the difference in probability/score between
# the winning class and the second best class. We only use
# probability if the classifier's predict function supports it.
delta_prob <- 1
if(!is.null(prob))
try({
if (any(rowSums(prob) != 1))
prob <- cbind(prob, 1 - rowSums(prob))
max_prob <- t(apply(prob, MARGIN = 1, sort, decreasing = TRUE))
delta_prob <- max_prob[,1] - max_prob[,2]
}, silent = TRUE)
cl <- factor(cl, levels = levels(y))
g <- g |> add_column(prediction = cl,
delta_prob = delta_prob)
ggplot(g, mapping = aes(
x = .data[[colnames(g)[1]]],
y = .data[[colnames(g)[2]]])) +
geom_raster(mapping = aes(fill = prediction,
alpha = delta_prob)) +
geom_contour(mapping = aes(z = as.numeric(prediction)),
bins = length(levels(cl)),
linewidth = .5,
color = "black") +
geom_point(data = data, mapping = aes(
x = .data[[colnames(data)[1]]],
y = .data[[colnames(data)[2]]],
shape = .data[[class_var]]),
alpha = .7) +
scale_alpha_continuous(range = c(0,1),
limits = c(0,1)) +
labs(subtitle = paste("Training accuracy:", round(acc, 2)))
}4.12.1 Iris Dataset
For easier visualization, we use two dimensions of the Iris dataset.
set.seed(1000)
data(iris)
iris <- as_tibble(iris)
x <- iris |> dplyr::select(Sepal.Length, Sepal.Width, Species)
# Note: package MASS overwrites the select function.
x
## # A tibble: 150 × 3
## Sepal.Length Sepal.Width Species
## <dbl> <dbl> <fct>
## 1 5.1 3.5 setosa
## 2 4.9 3 setosa
## 3 4.7 3.2 setosa
## 4 4.6 3.1 setosa
## 5 5 3.6 setosa
## 6 5.4 3.9 setosa
## 7 4.6 3.4 setosa
## 8 5 3.4 setosa
## 9 4.4 2.9 setosa
## 10 4.9 3.1 setosa
## # ℹ 140 more rows
ggplot(x, aes(x = Sepal.Length,
y = Sepal.Width,
fill = Species)) +
stat_density_2d(geom = "polygon",
aes(alpha = after_stat(level))) +
geom_point()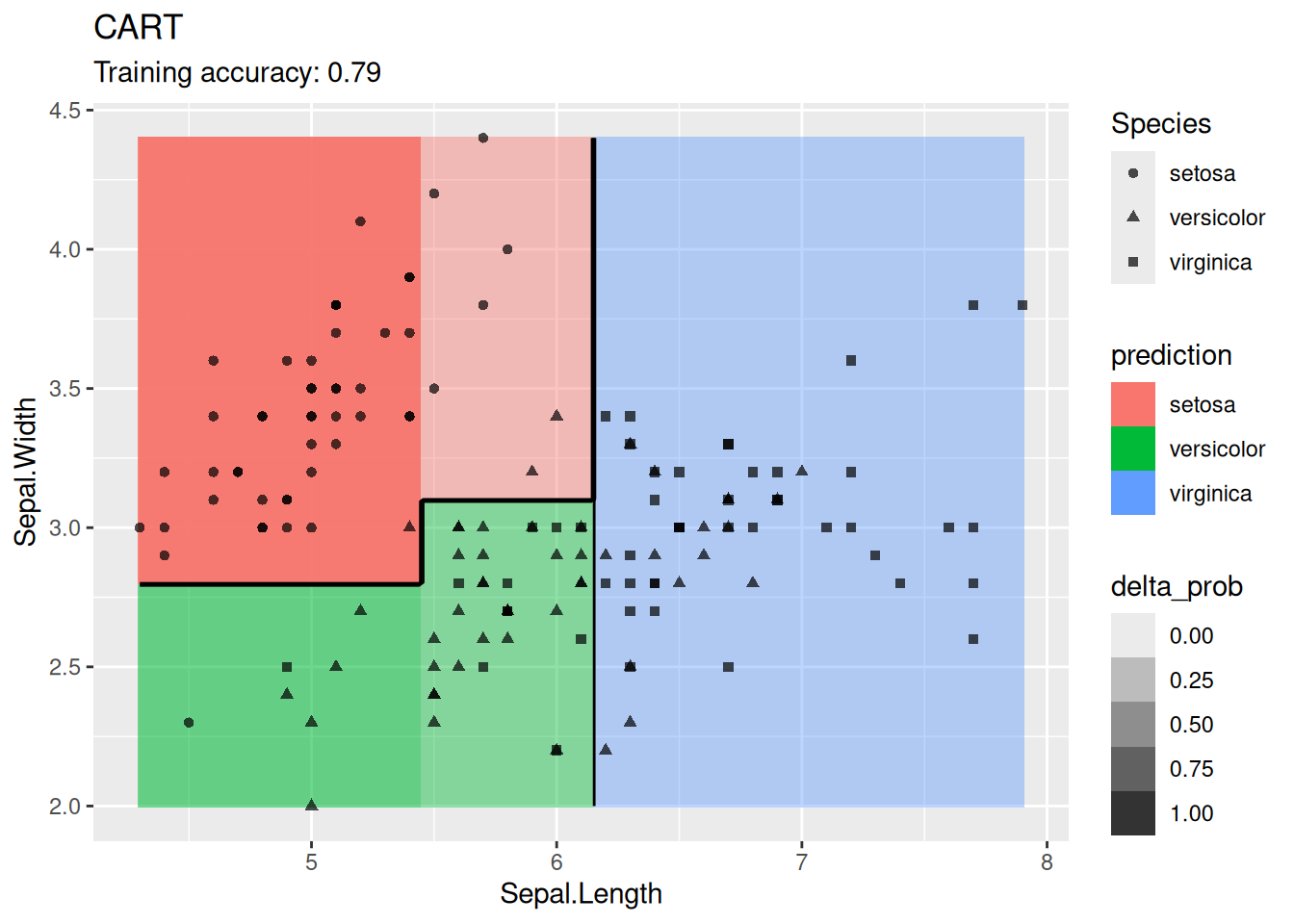
This is the original data.
Color is used to show the density.
Note that there is some overplotting with several points in the same position.
You could use geom_jitter() instead of geom_point().
4.12.1.1 Nearest Neighbor Classifier
We try several values for \(k\).
model <- x |> caret::knn3(Species ~ ., data = _, k = 1)
decisionplot(model, x, class_var = "Species") +
labs(title = "kNN (1 neighbor)")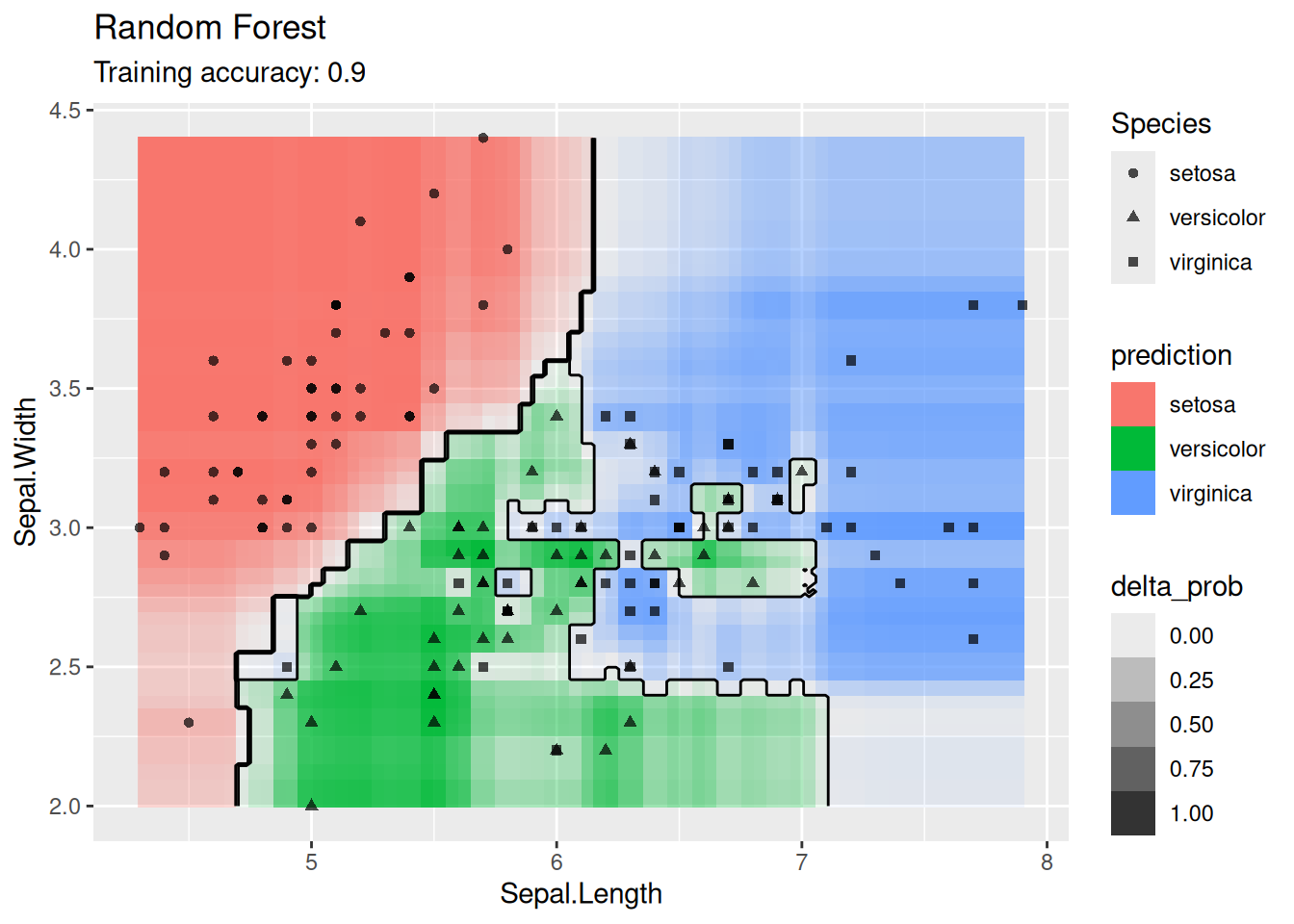
model <- x |> caret::knn3(Species ~ ., data = _, k = 3)
decisionplot(model, x, class_var = "Species") +
labs(title = "kNN (3 neighbors)")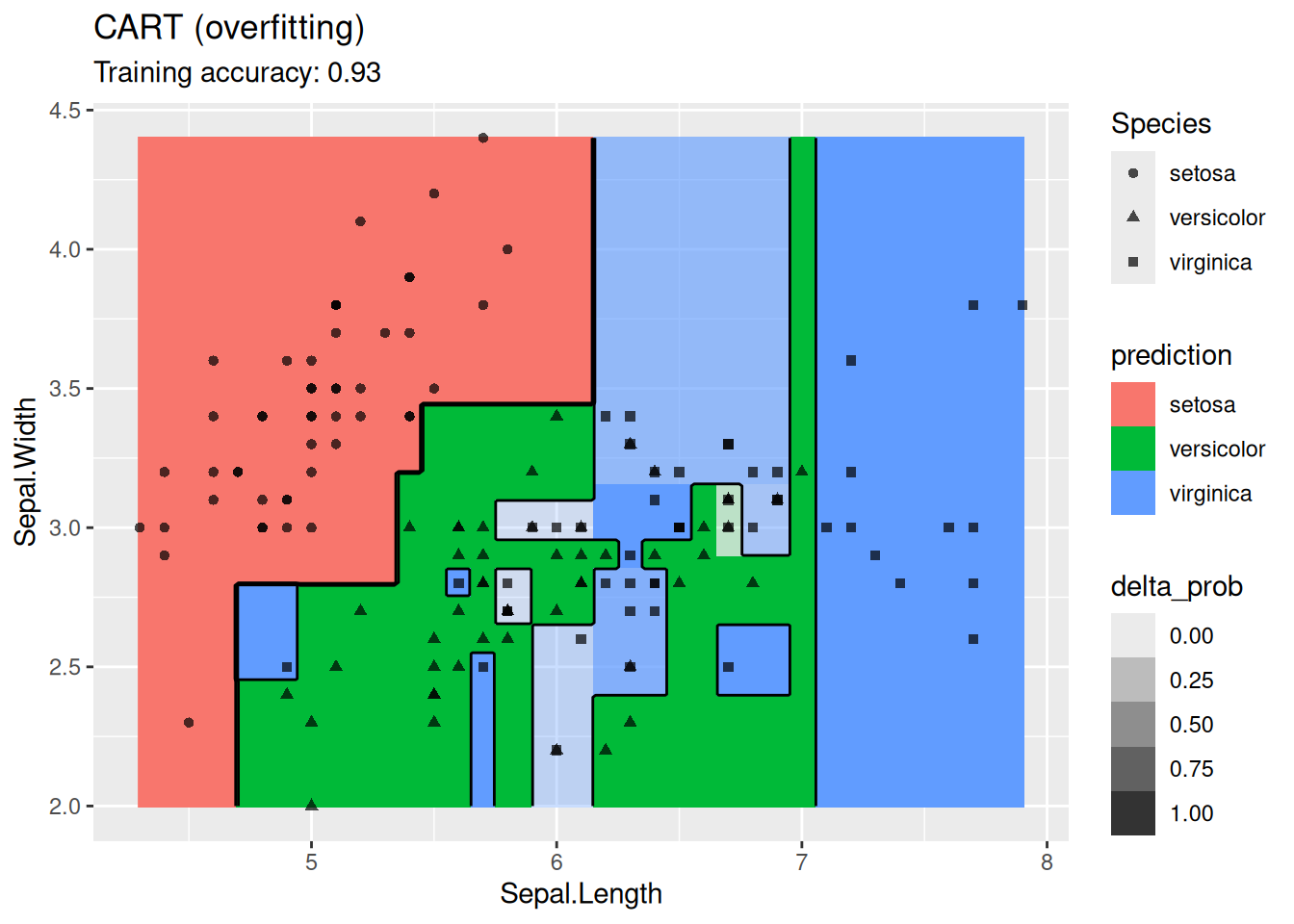
model <- x |> caret::knn3(Species ~ ., data = _, k = 9)
decisionplot(model, x, class_var = "Species") +
labs(title = "kNN (9 neighbors)")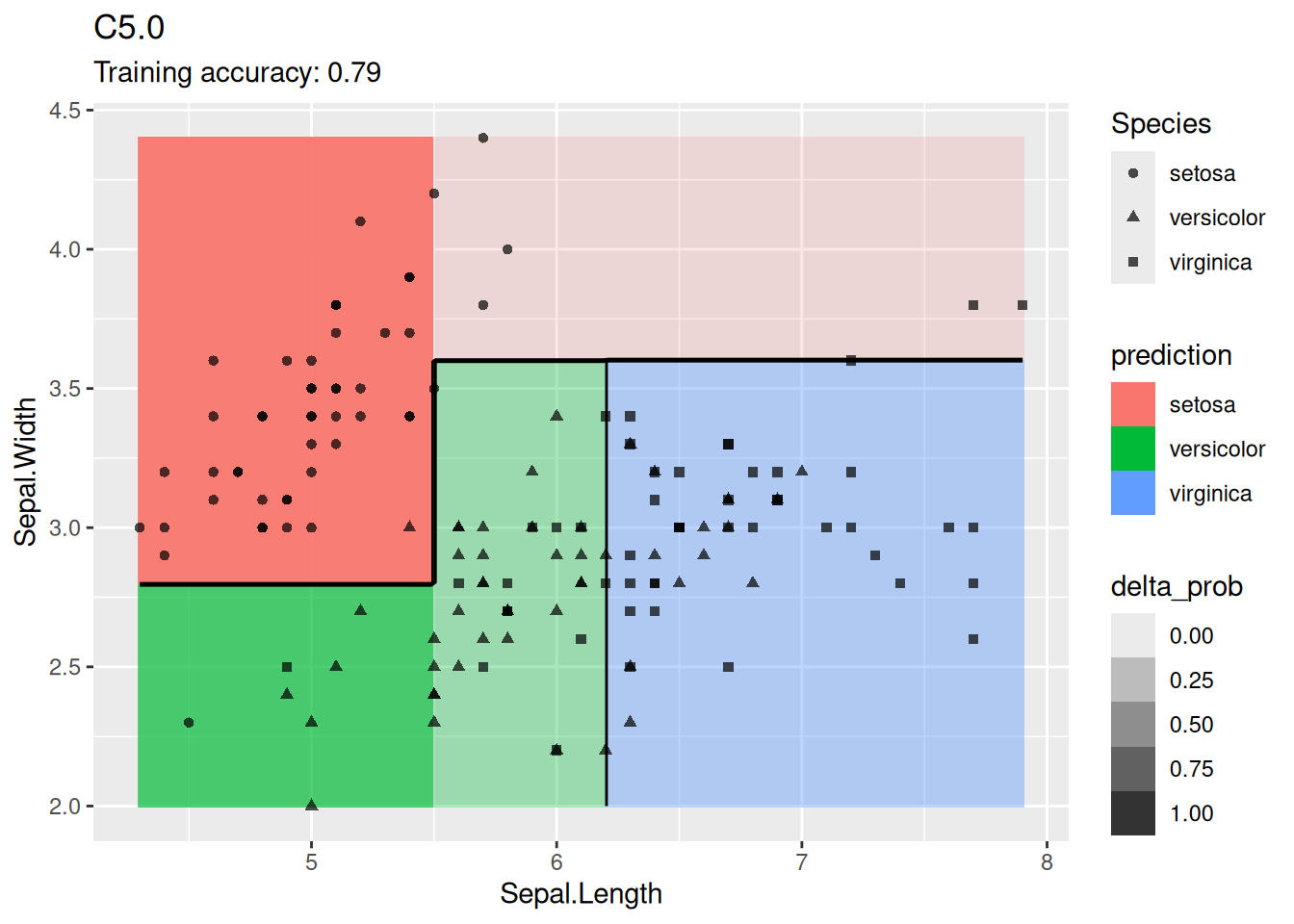
Increasing \(k\) smooths the decision boundary. At \(k=1\), we see white areas around points where flowers of two classes are in the same spot. Here, the algorithm randomly chooses a class during prediction resulting in the meandering decision boundary. The predictions in that area are not stable and every time we ask for a class, we may get a different class.
Note: The crazy lines in white areas are an artifact of the visualization. Here the classifier randomly selects a class.
4.12.1.2 Naive Bayes Classifier
Use a Gaussian naive Bayes classifier.
model <- x |> e1071::naiveBayes(Species ~ ., data = _)
decisionplot(model, x, class_var = "Species",
predict_type = c("class", "raw")) +
labs(title = "Naive Bayes")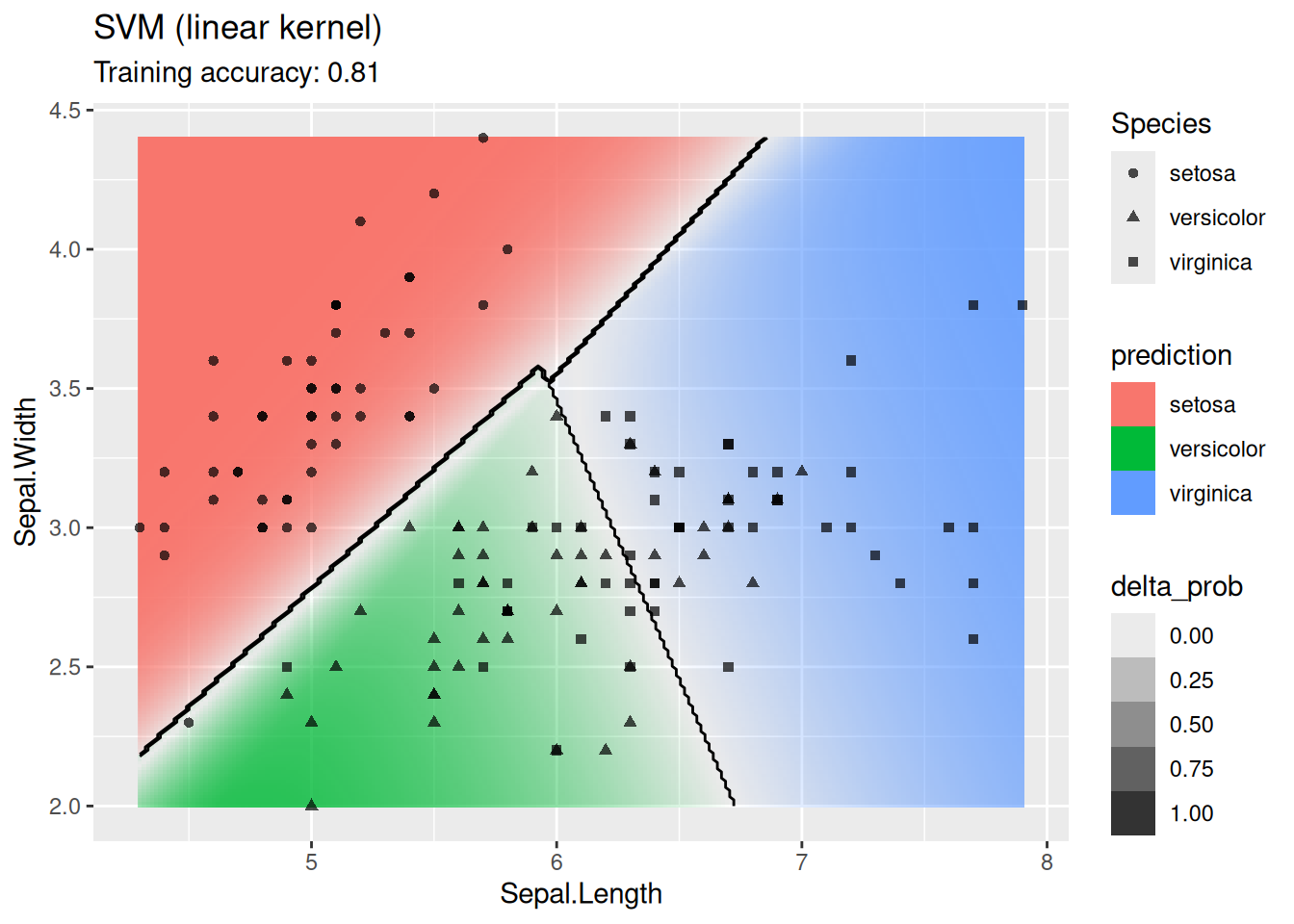
The GBN finds a good model with the advantage that no hyperparameters are needed.
4.12.1.3 Linear Discriminant Analysis
LDA finds linear decision boundaries.
model <- x |> MASS::lda(Species ~ ., data = _)
decisionplot(model, x, class_var = "Species") +
labs(title = "LDA")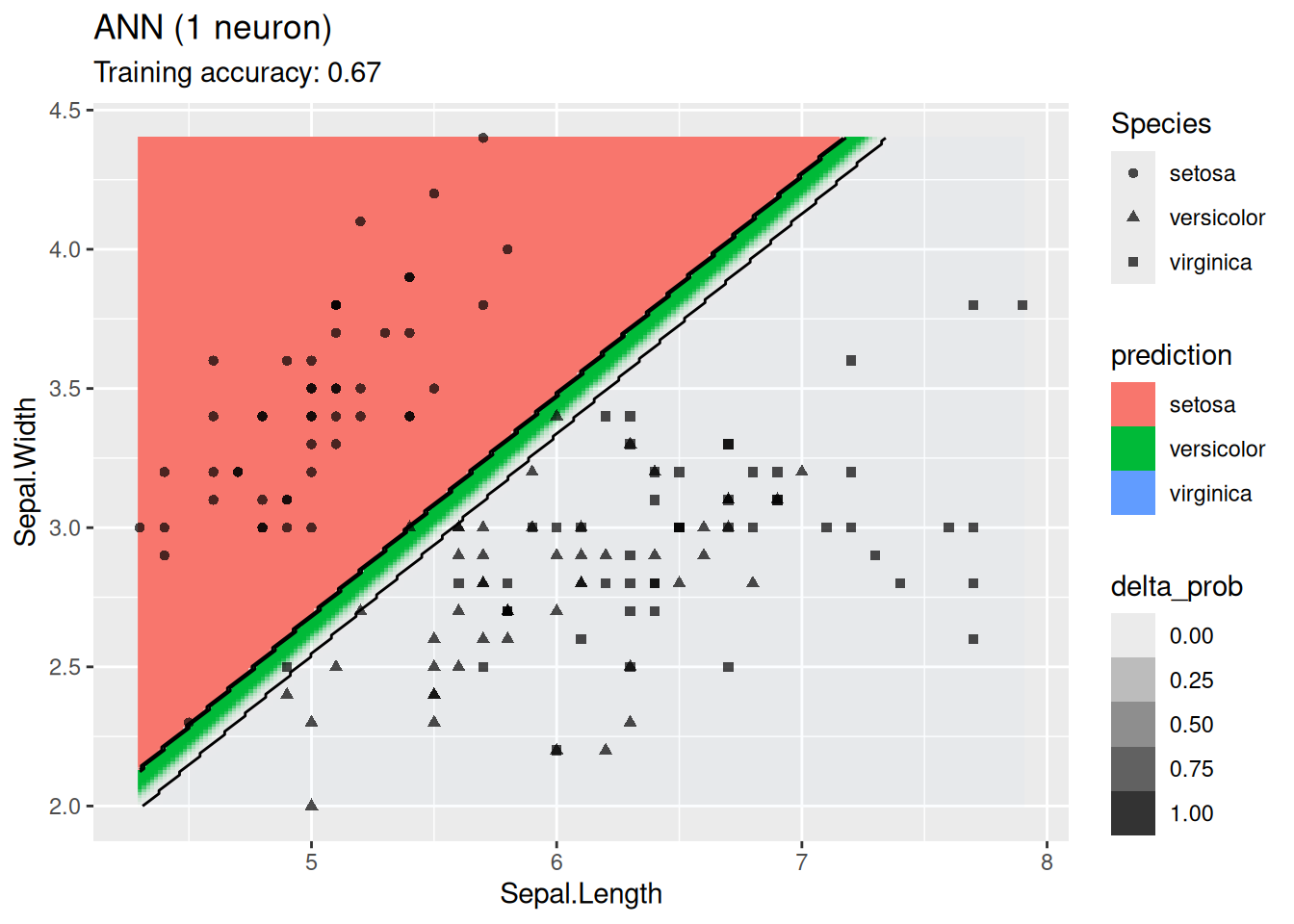
Linear decision boundaries work for this dataset so LDA works well.
4.12.1.4 Multinomial Logistic Regression
Multinomial logistic regression is an extension of logistic regression to problems with more than two classes.
model <- x |> nnet::multinom(Species ~., data = _)
## # weights: 12 (6 variable)
## initial value 164.791843
## iter 10 value 62.715967
## iter 20 value 59.808291
## iter 30 value 55.445984
## iter 40 value 55.375704
## iter 50 value 55.346472
## iter 60 value 55.301707
## iter 70 value 55.253532
## iter 80 value 55.243230
## iter 90 value 55.230241
## iter 100 value 55.212479
## final value 55.212479
## stopped after 100 iterations
decisionplot(model, x, class_var = "Species") +
labs(titel = "Multinomial Logistic Regression")
## Ignoring unknown labels:
## • titel : "Multinomial Logistic Regression"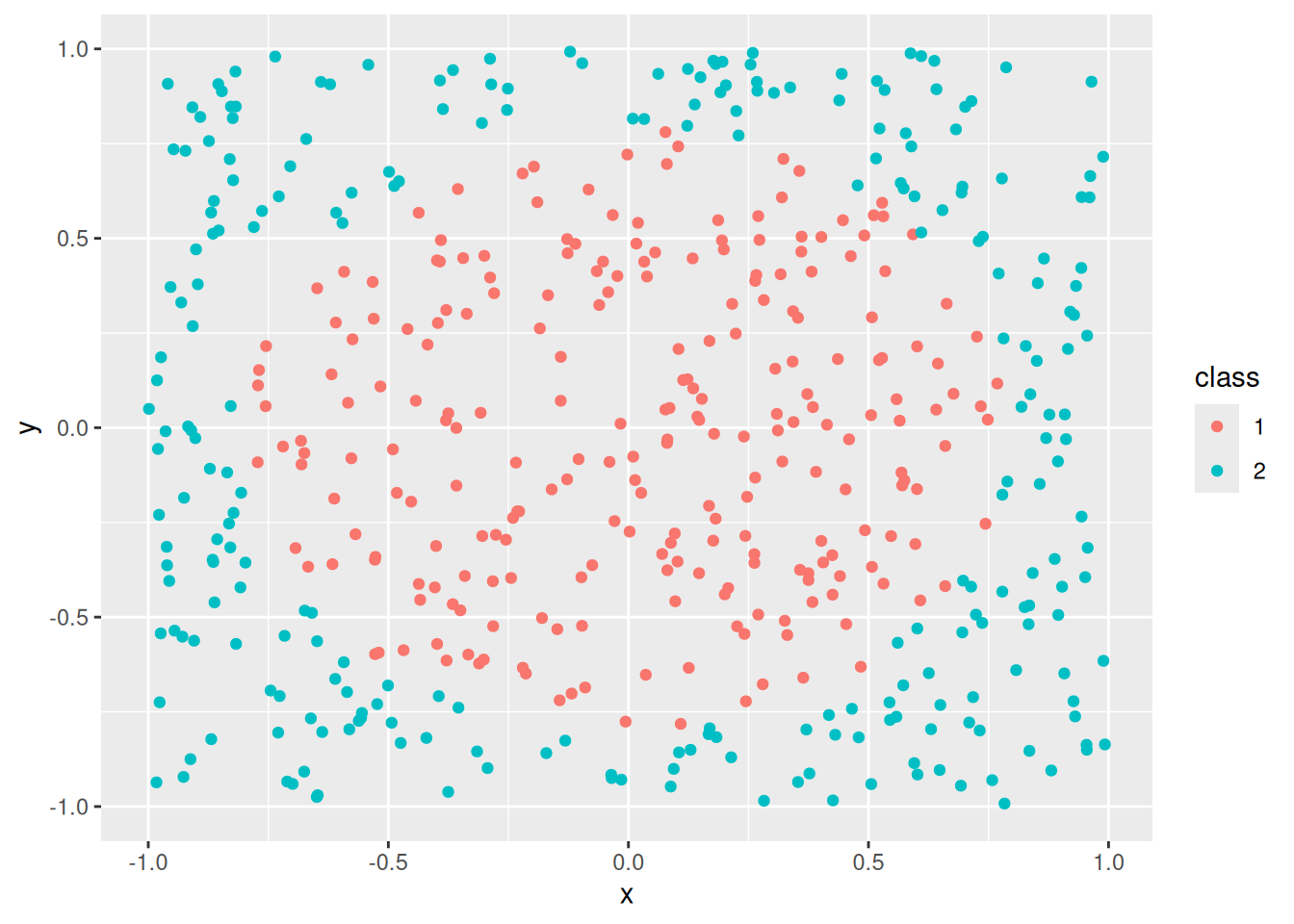
4.12.1.5 Decision Trees
Compare different types of decision trees.
model <- x |> rpart::rpart(Species ~ ., data = _)
decisionplot(model, x, class_var = "Species") +
labs(title = "CART")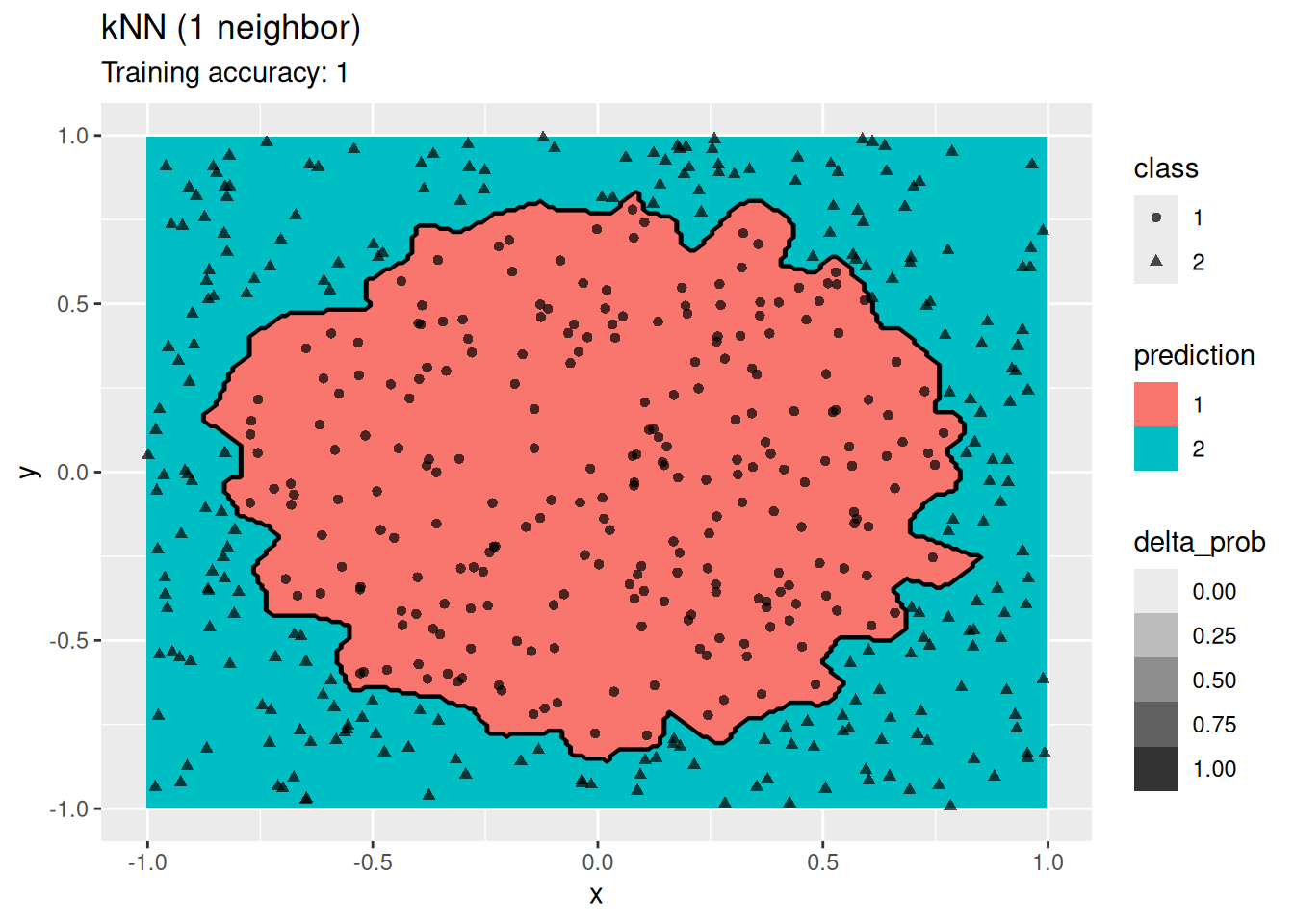
model <- x |> rpart::rpart(Species ~ ., data = _,
control = rpart::rpart.control(cp = 0.001, minsplit = 1))
decisionplot(model, x, class_var = "Species") +
labs(title = "CART (overfitting)")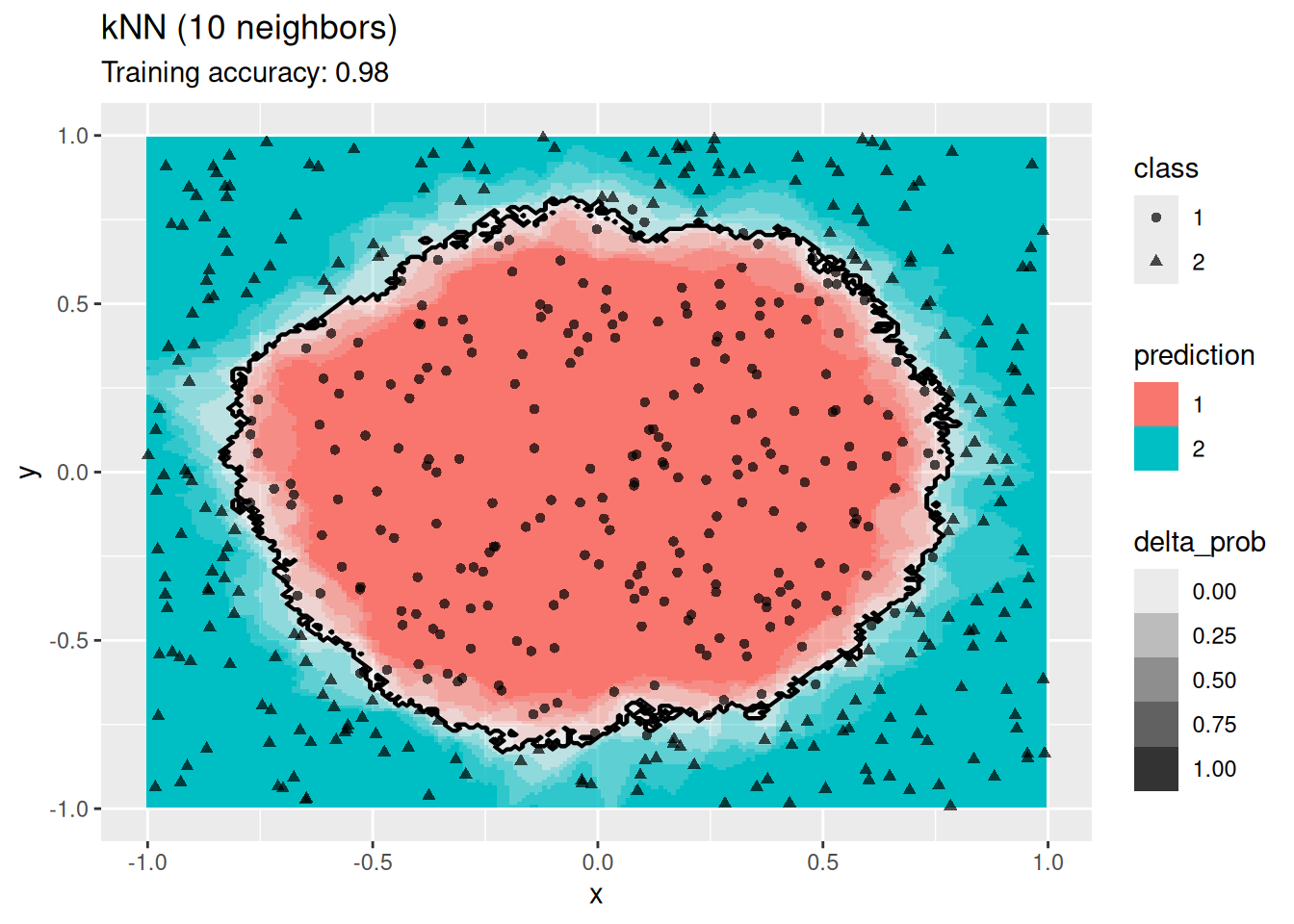
model <- x |> C50::C5.0(Species ~ ., data = _)
decisionplot(model, x, class_var = "Species") +
labs(title = "C5.0")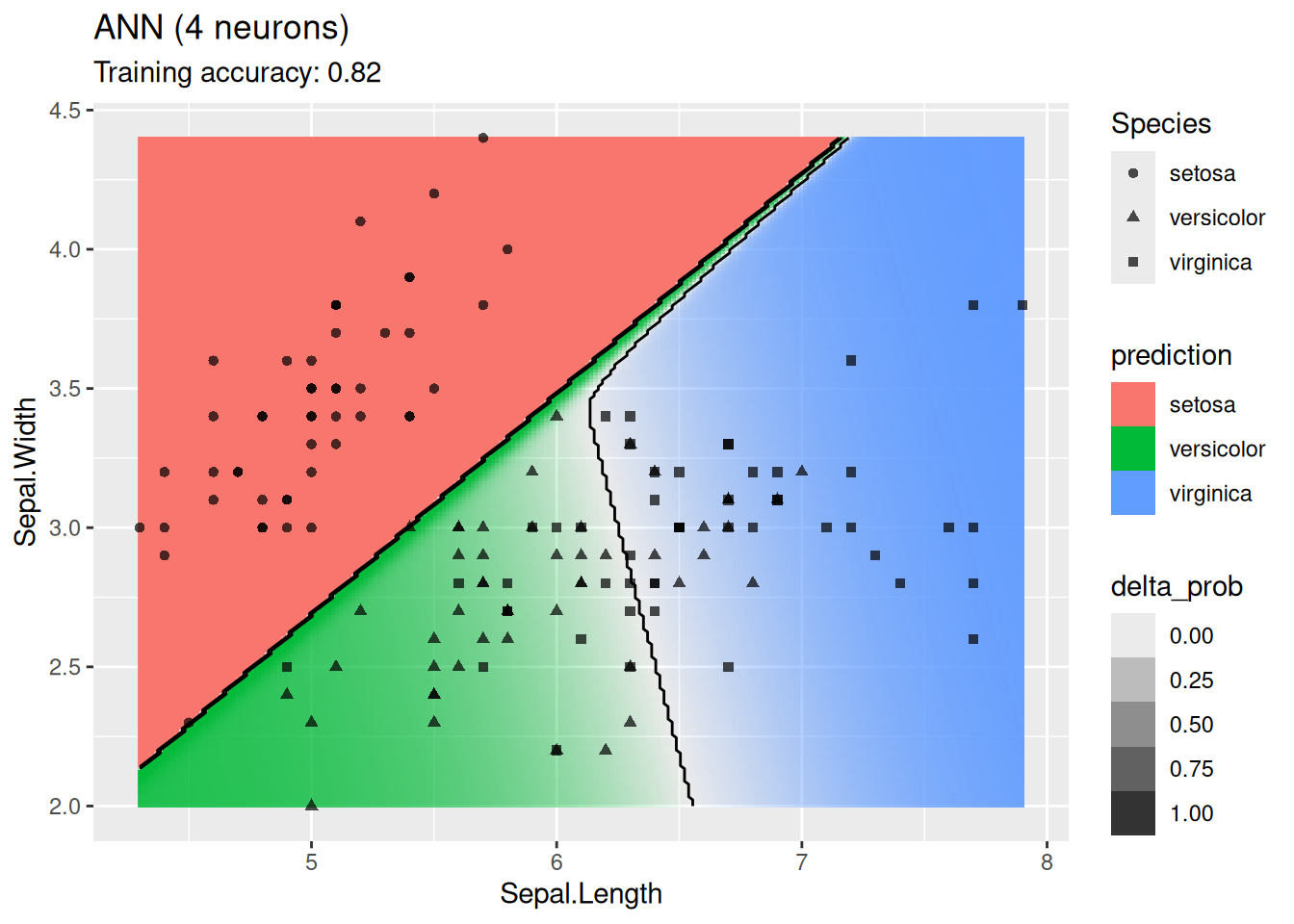
4.12.1.6 Ensemble: Random Forest
Use an ensemble method.
model <- x |> randomForest::randomForest(Species ~ ., data = _)
decisionplot(model, x, class_var = "Species") +
labs(title = "Random Forest")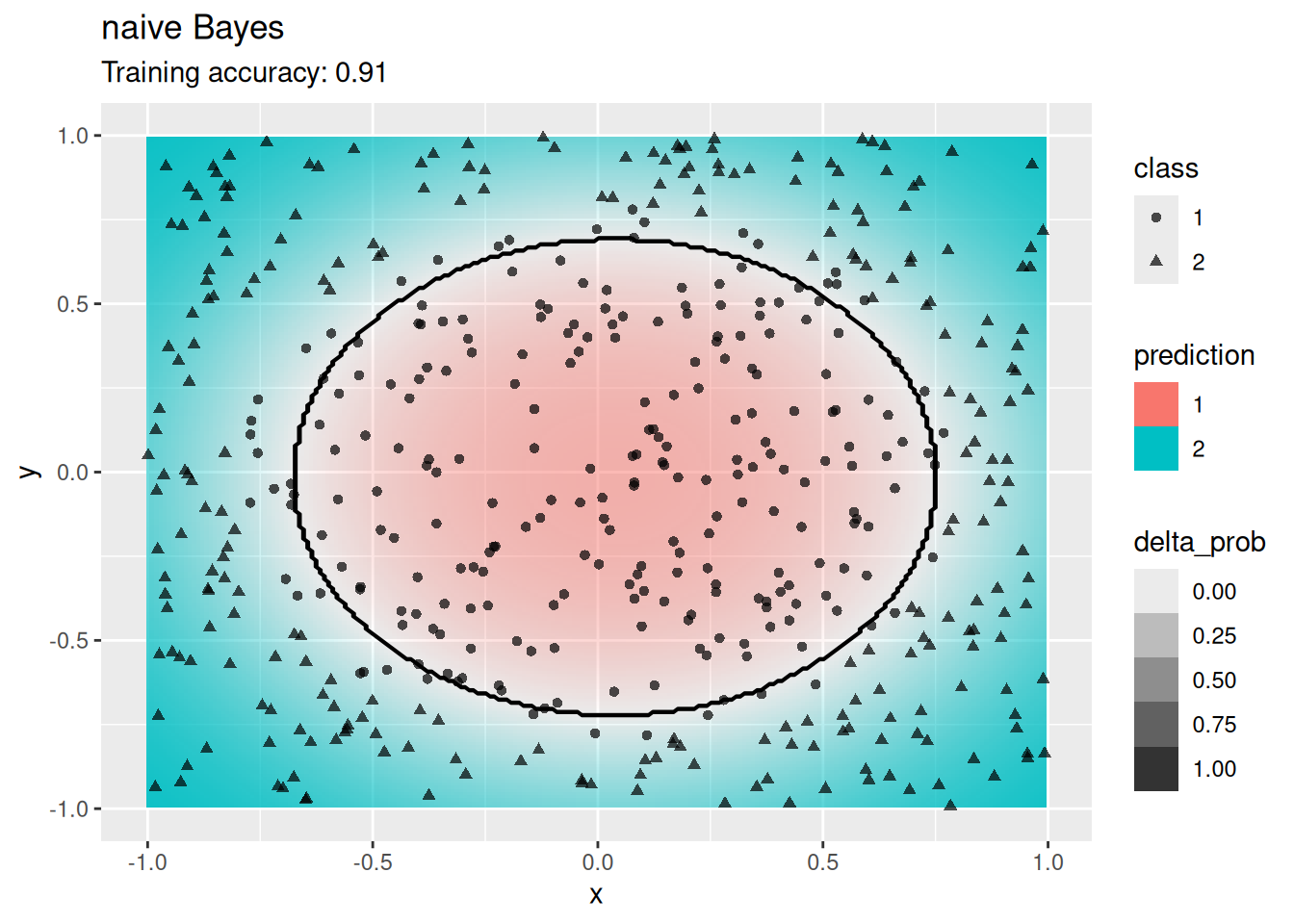
For the default settings for Random forest, the model seems to overfit the training data. More data would probably alleviate this issue.
4.12.1.7 Support Vector Machine
Compare SVMs with different kernel functions.
model <- x |> e1071::svm(Species ~ ., data = _,
kernel = "linear", probability = TRUE)
decisionplot(model, x, class_var = "Species") +
labs(title = "SVM (linear kernel)")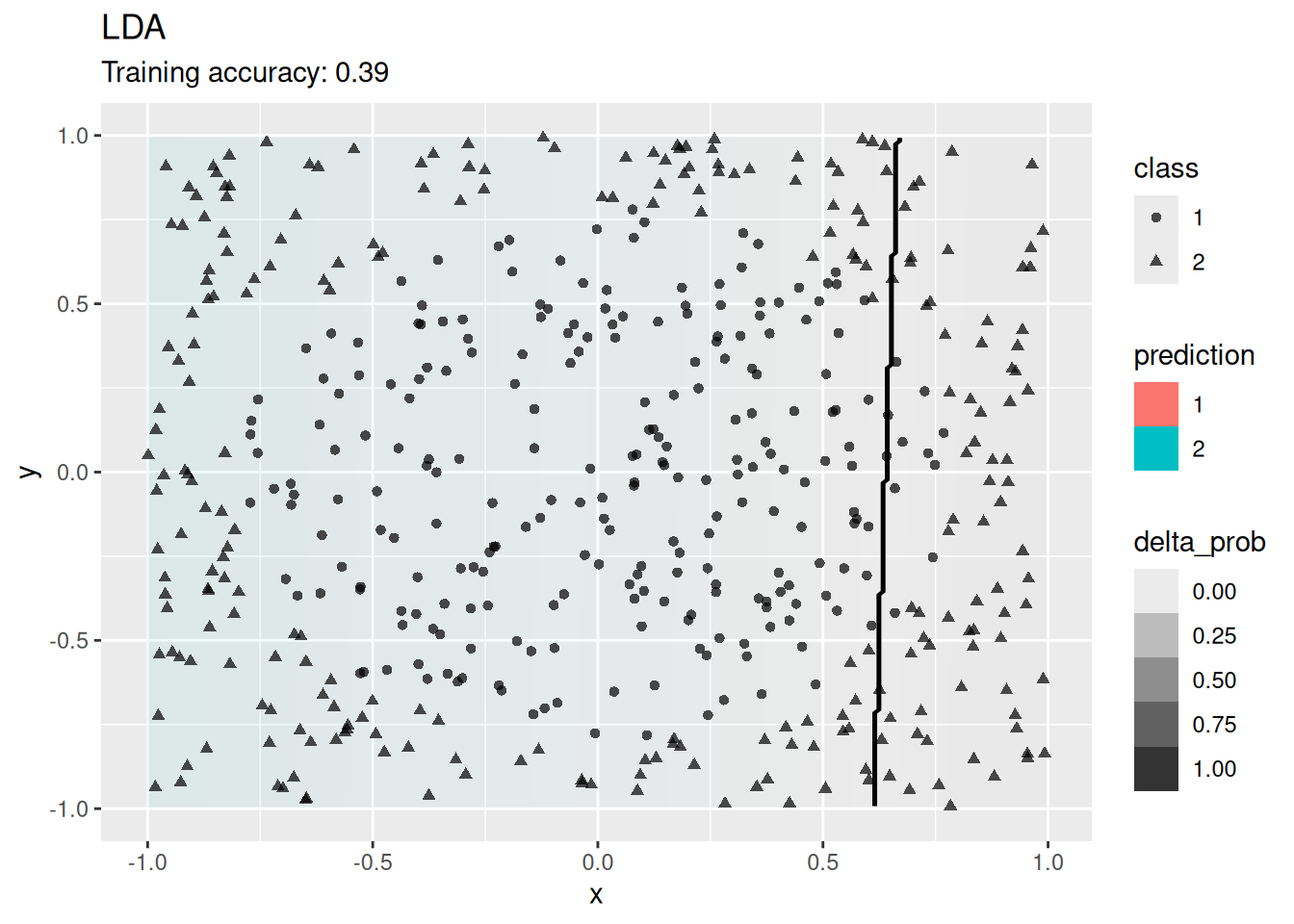
model <- x |> e1071::svm(Species ~ ., data = _,
kernel = "radial", probability = TRUE)
decisionplot(model, x, class_var = "Species") +
labs(title = "SVM (radial kernel)")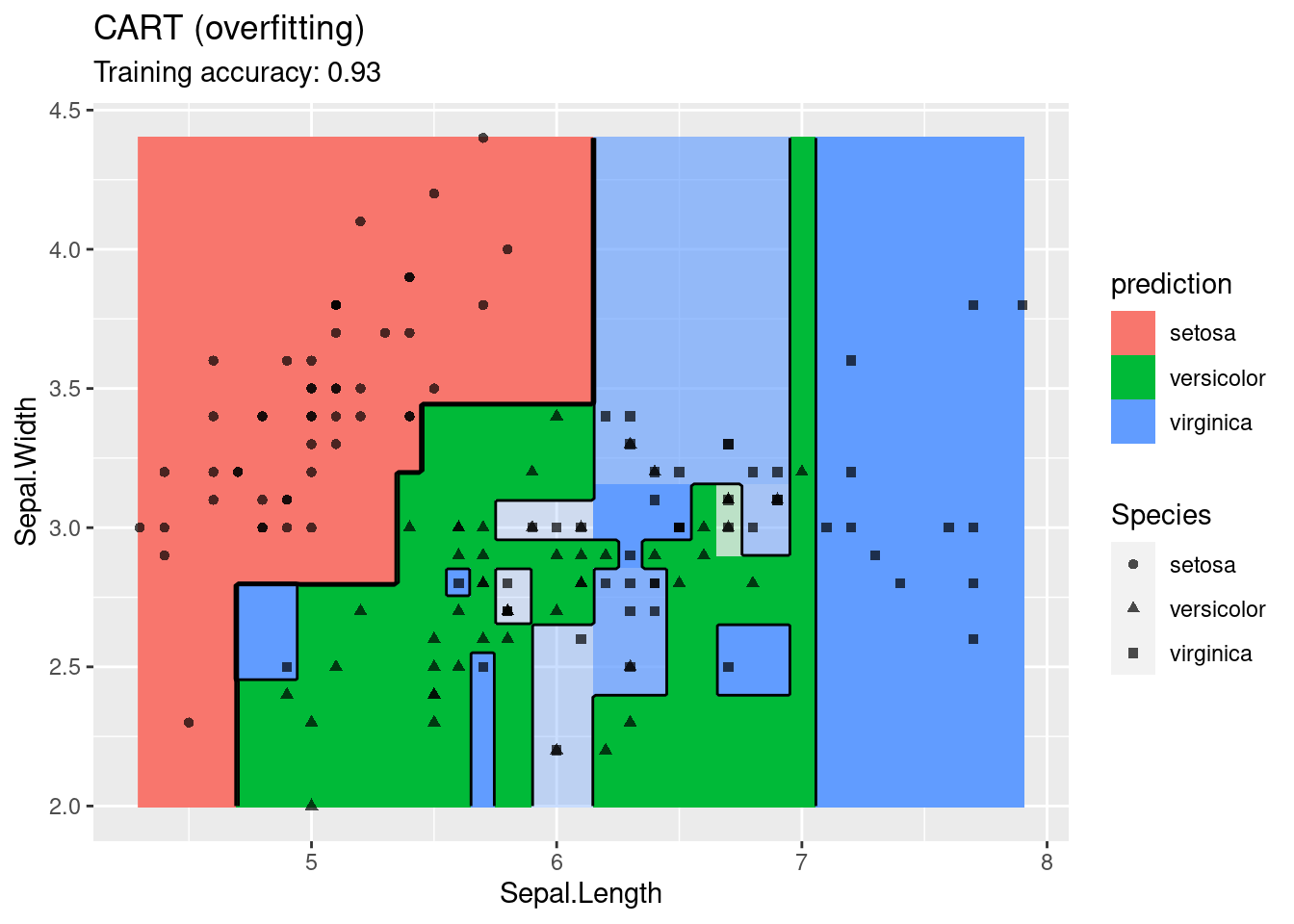
model <- x |> e1071::svm(Species ~ ., data = _,
kernel = "polynomial", probability = TRUE)
decisionplot(model, x, class_var = "Species") +
labs(title = "SVM (polynomial kernel)")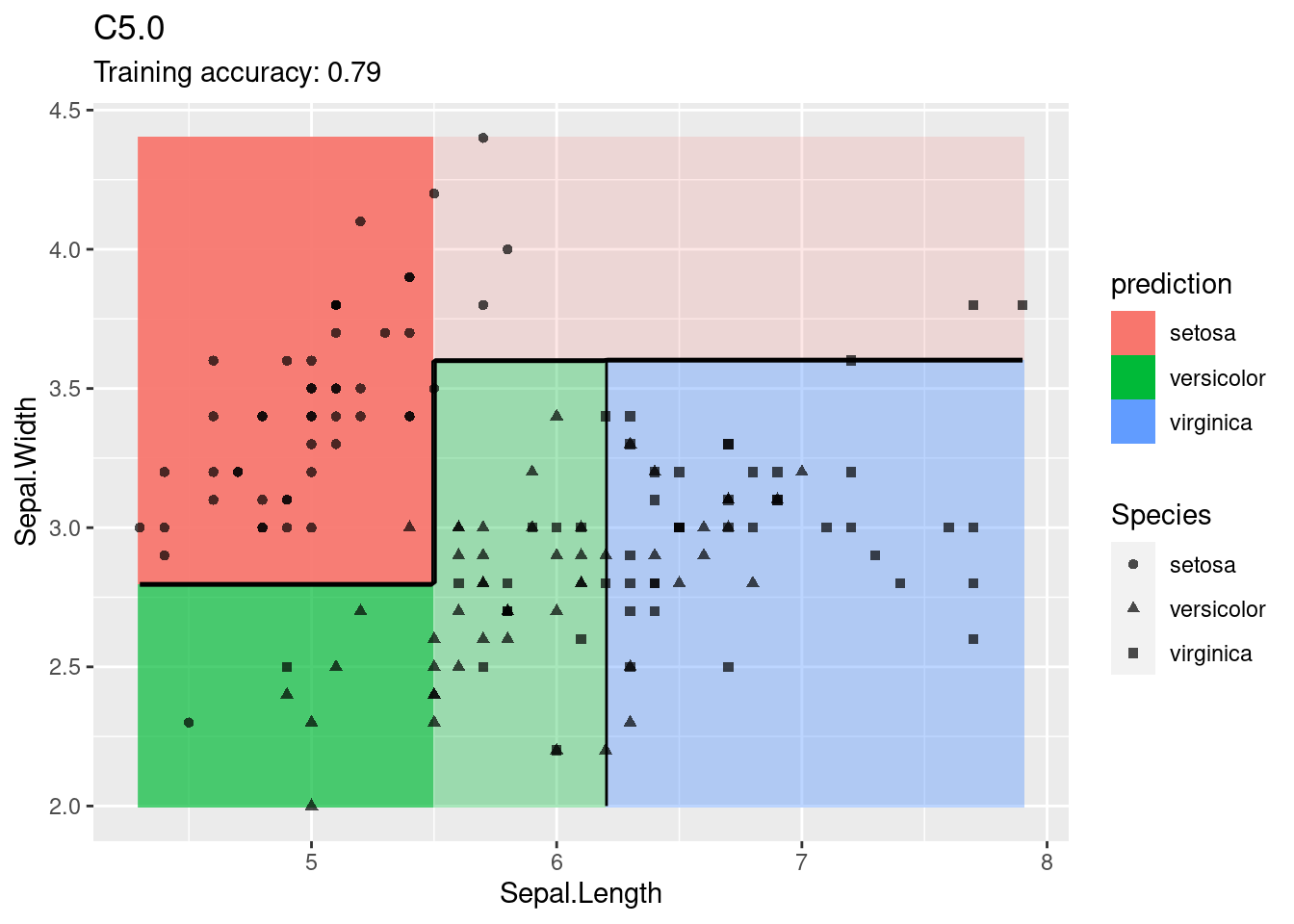
model <- x |> e1071::svm(Species ~ ., data = _,
kernel = "sigmoid", probability = TRUE)
decisionplot(model, x, class_var = "Species") +
labs(title = "SVM (sigmoid kernel)")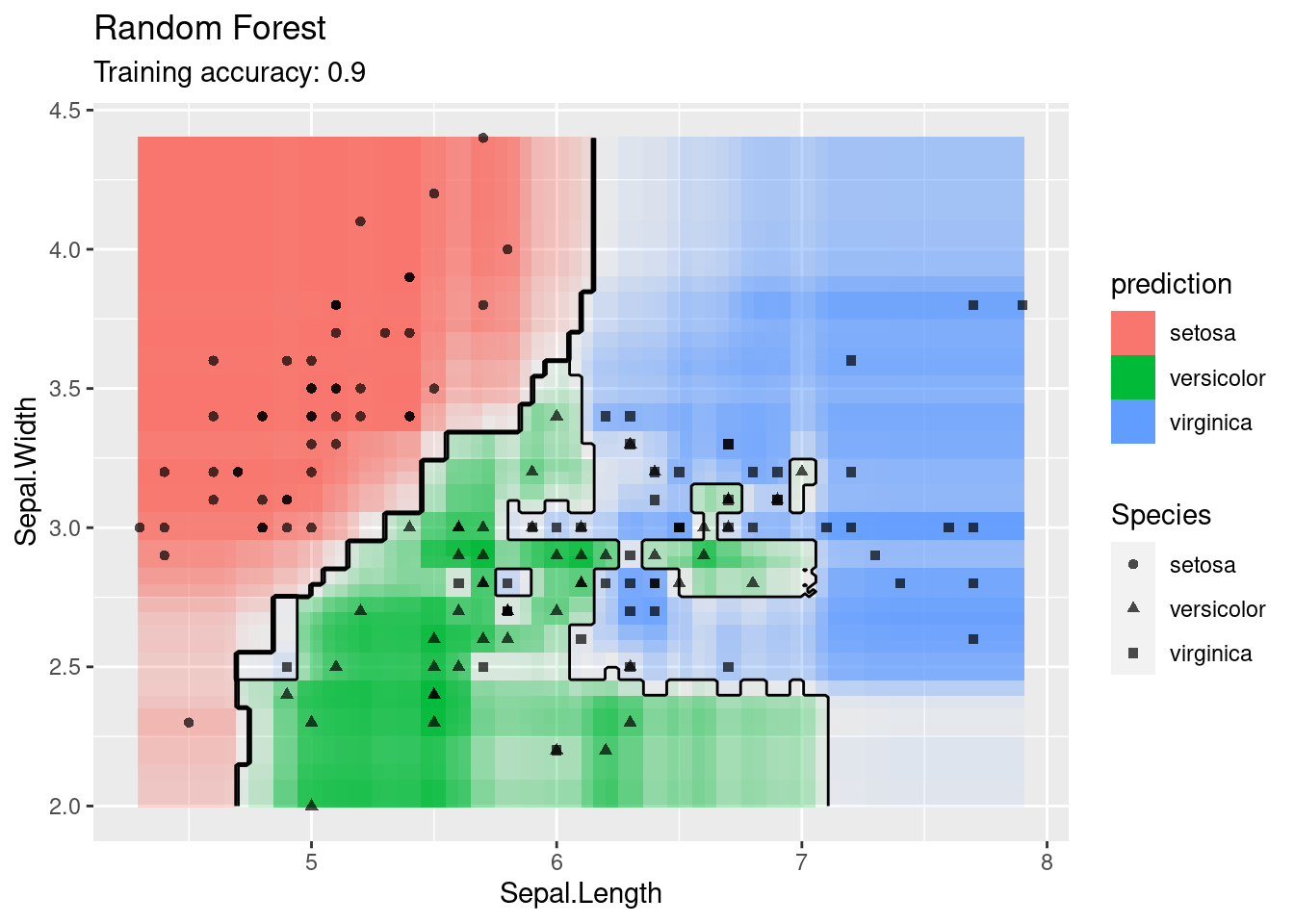
The linear SVM (without a kernel) produces straight lines and works well on the iris data. Most kernels do also well, only the sigmoid kernel seems to find a very strange decision boundary which indicates that the data does not have a linear decision boundary in the projected space.
4.12.1.8 Single Layer Feed-forward Neural Networks
Use a simple network with one hidden layer. We will try a different number of neurons for the hidden layer.
set.seed(1234)
model <- x |> nnet::nnet(Species ~ ., data = _,
size = 1, trace = FALSE)
decisionplot(model, x, class_var = "Species",
predict_type = c("class", "raw")) +
labs(title = "ANN (1 neuron)")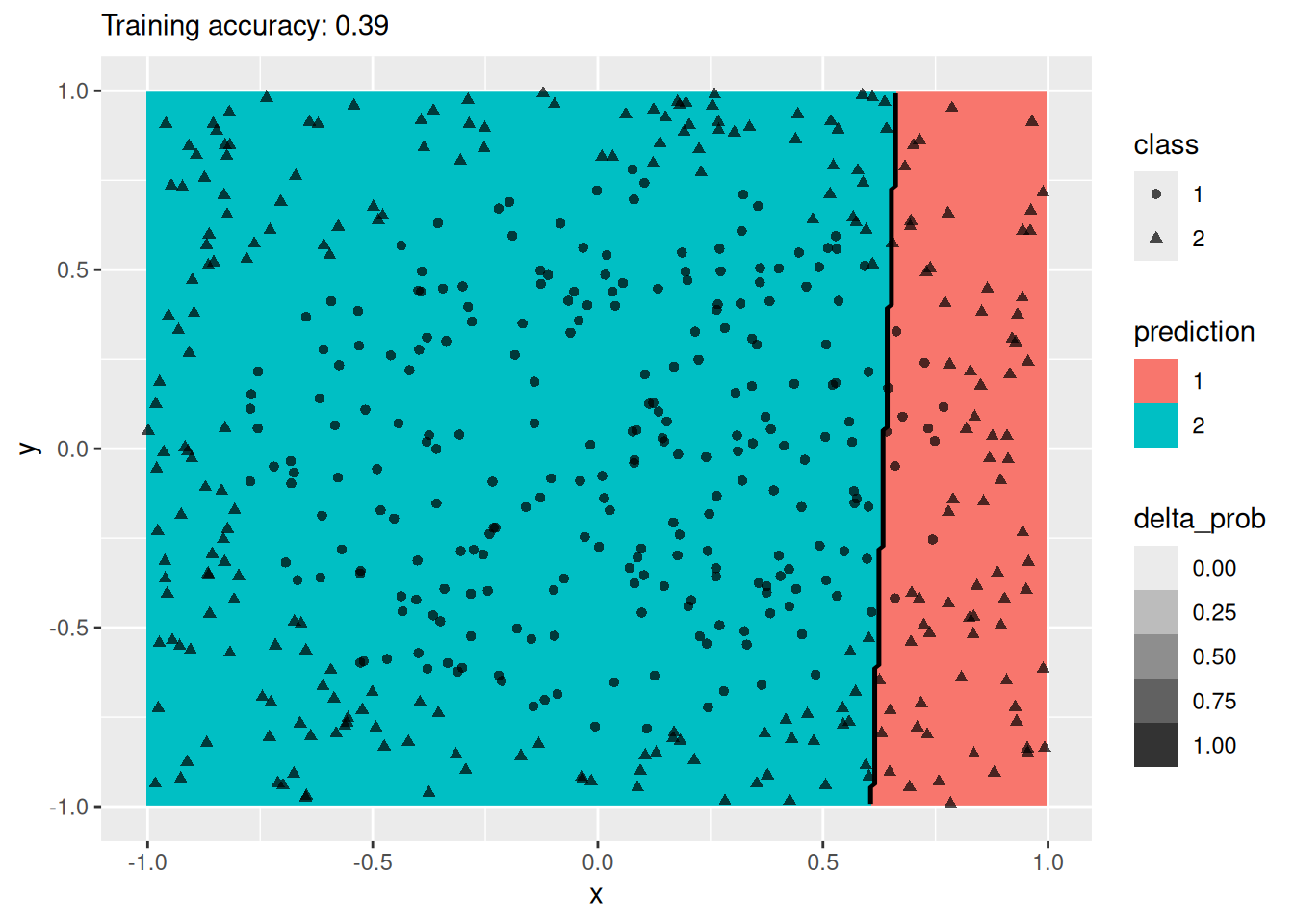
model <- x |> nnet::nnet(Species ~ ., data = _,
size = 2, trace = FALSE)
decisionplot(model, x, class_var = "Species",
predict_type = c("class", "raw")) +
labs(title = "ANN (2 neurons)")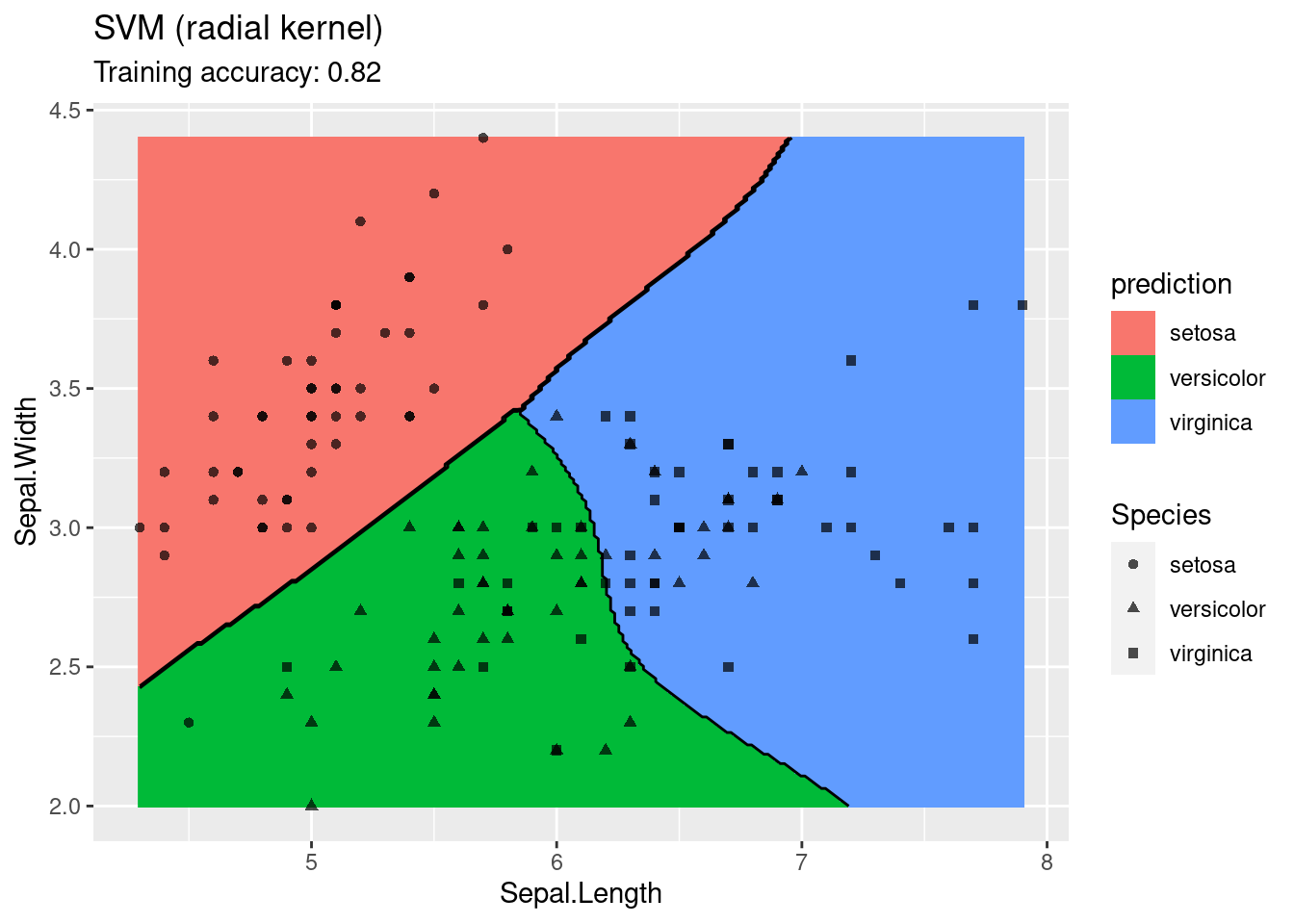
model <- x |> nnet::nnet(Species ~ ., data = _,
size = 4, trace = FALSE)
decisionplot(model, x, class_var = "Species",
predict_type = c("class", "raw")) +
labs(title = "ANN (4 neurons)")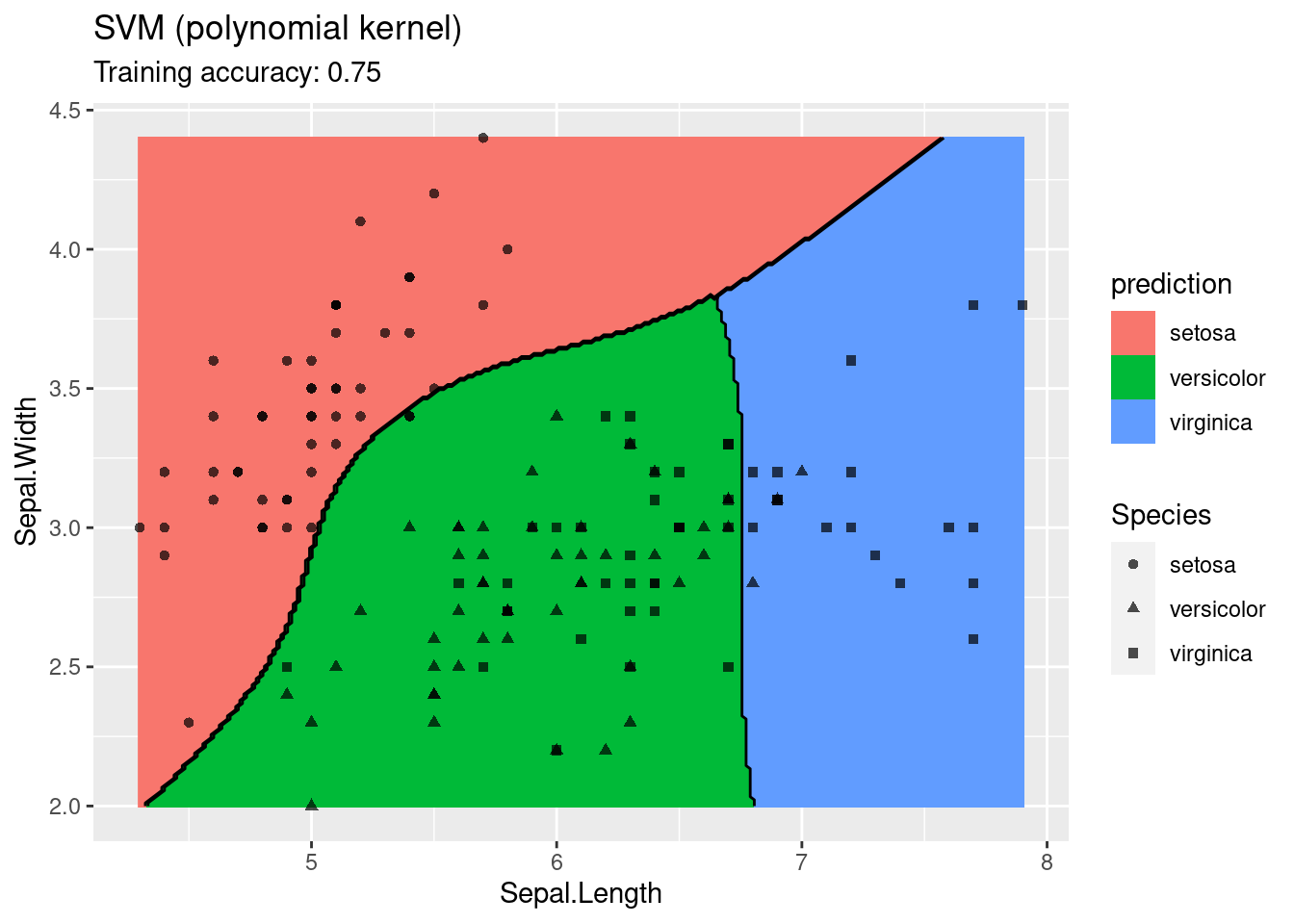
model <- x |> nnet::nnet(Species ~ ., data = _,
size = 6, trace = FALSE)
decisionplot(model, x, class_var = "Species",
predict_type = c("class", "raw")) +
labs(title = "ANN (6 neurons)")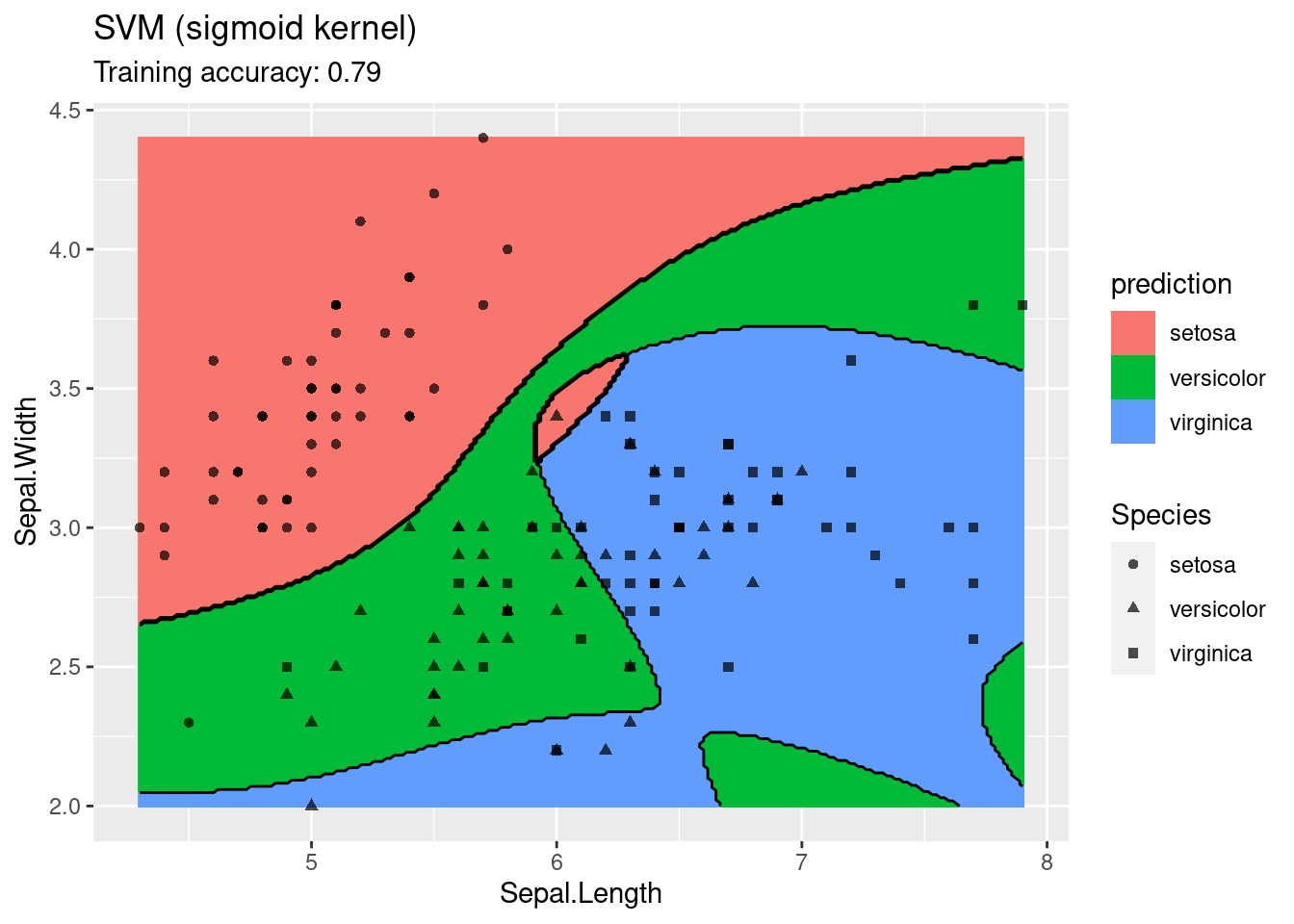
model <- x |> nnet::nnet(Species ~ ., data = _,
size = 20, trace = FALSE)
decisionplot(model, x, class_var = "Species",
predict_type = c("class", "raw")) +
labs(title = "ANN (20 neurons)")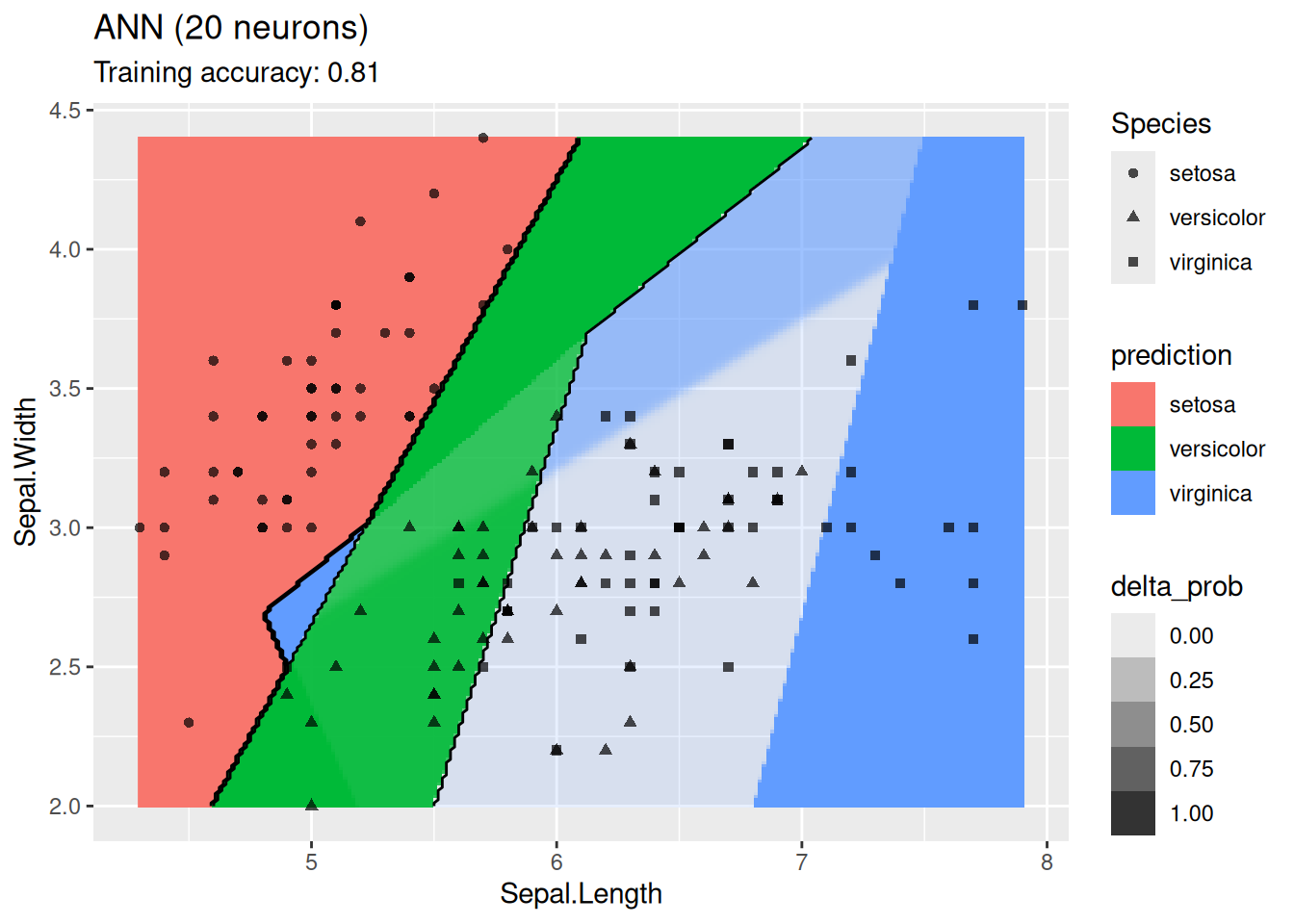
model <- x |> nnet::nnet(Species ~ ., data = _,
size = 100, trace = FALSE)
decisionplot(model, x, class_var = "Species",
predict_type = c("class", "raw")) +
labs(title = "ANN (100 neurons)")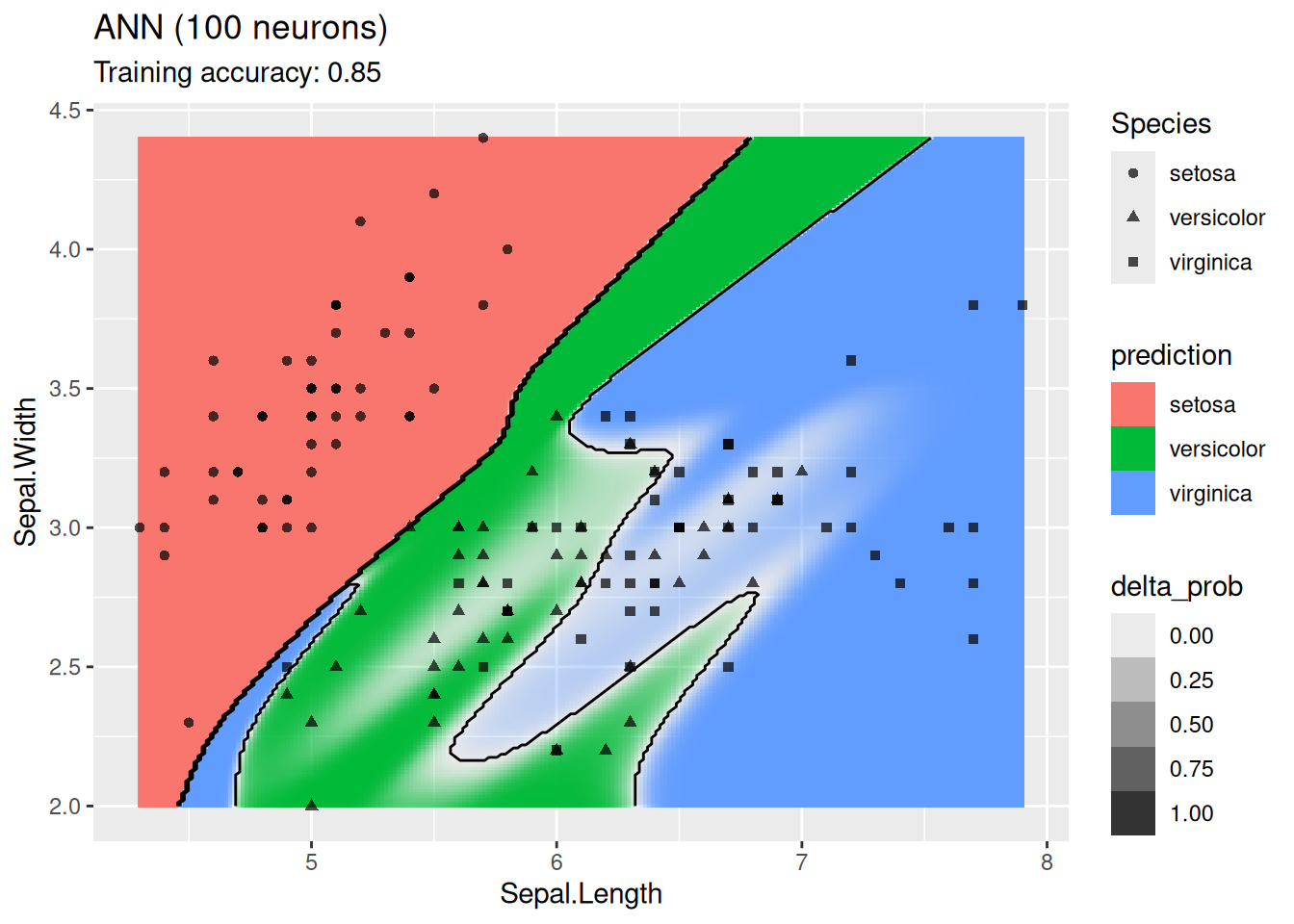
model <- x |> nnet::nnet(Species ~ ., data = _,
size = 100, trace = FALSE)
decisionplot(model, x, class_var = "Species",
predict_type = c("class", "raw")) +
labs(title = "ANN 2nd try (100 neurons)")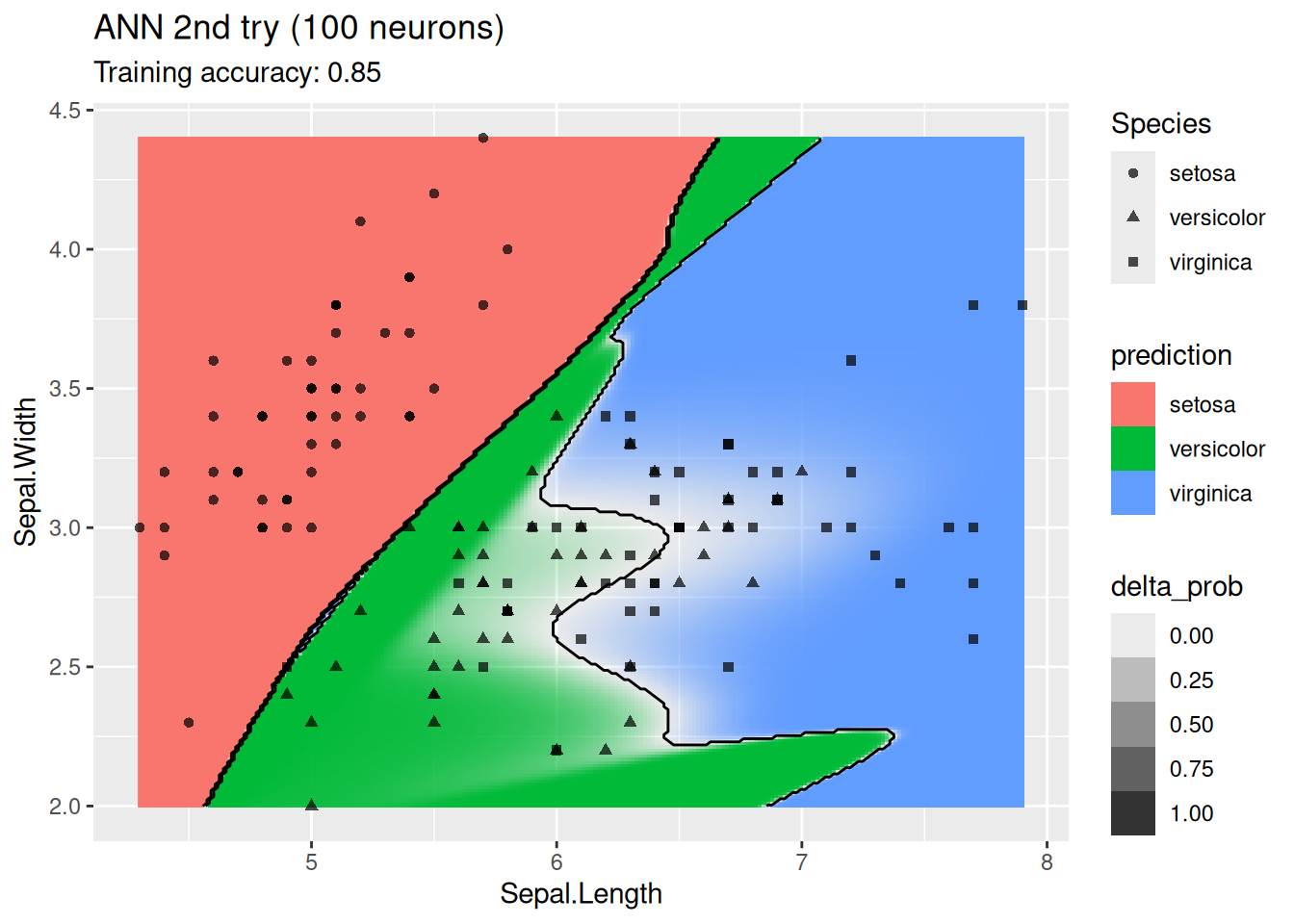
For this simple data set, 2 neurons produce the best classifier. The model starts to overfit with 6 or more neurons. I ran the ANN twice with 100 neurons, the two different decision boundaries indicate that the variability of the ANN with so many neurons is high.
4.12.2 Circle Dataset
set.seed(1000)
x <- mlbench::mlbench.circle(500)
# You can also experiment with the following datasets.
#x <- mlbench::mlbench.cassini(500)
#x <- mlbench::mlbench.spirals(500, sd = .1)
#x <- mlbench::mlbench.smiley(500)
x <- cbind(as.data.frame(x$x), factor(x$classes))
colnames(x) <- c("x", "y", "class")
x <- as_tibble(x)
x
## # A tibble: 500 × 3
## x y class
## <dbl> <dbl> <fct>
## 1 -0.344 0.448 1
## 2 0.518 0.915 2
## 3 -0.772 -0.0913 1
## 4 0.382 0.412 1
## 5 0.0328 0.438 1
## 6 -0.865 -0.354 2
## 7 0.477 0.640 2
## 8 0.167 -0.809 2
## 9 -0.568 -0.281 1
## 10 -0.488 0.638 2
## # ℹ 490 more rows
ggplot(x, aes(x = x, y = y, color = class)) +
geom_point()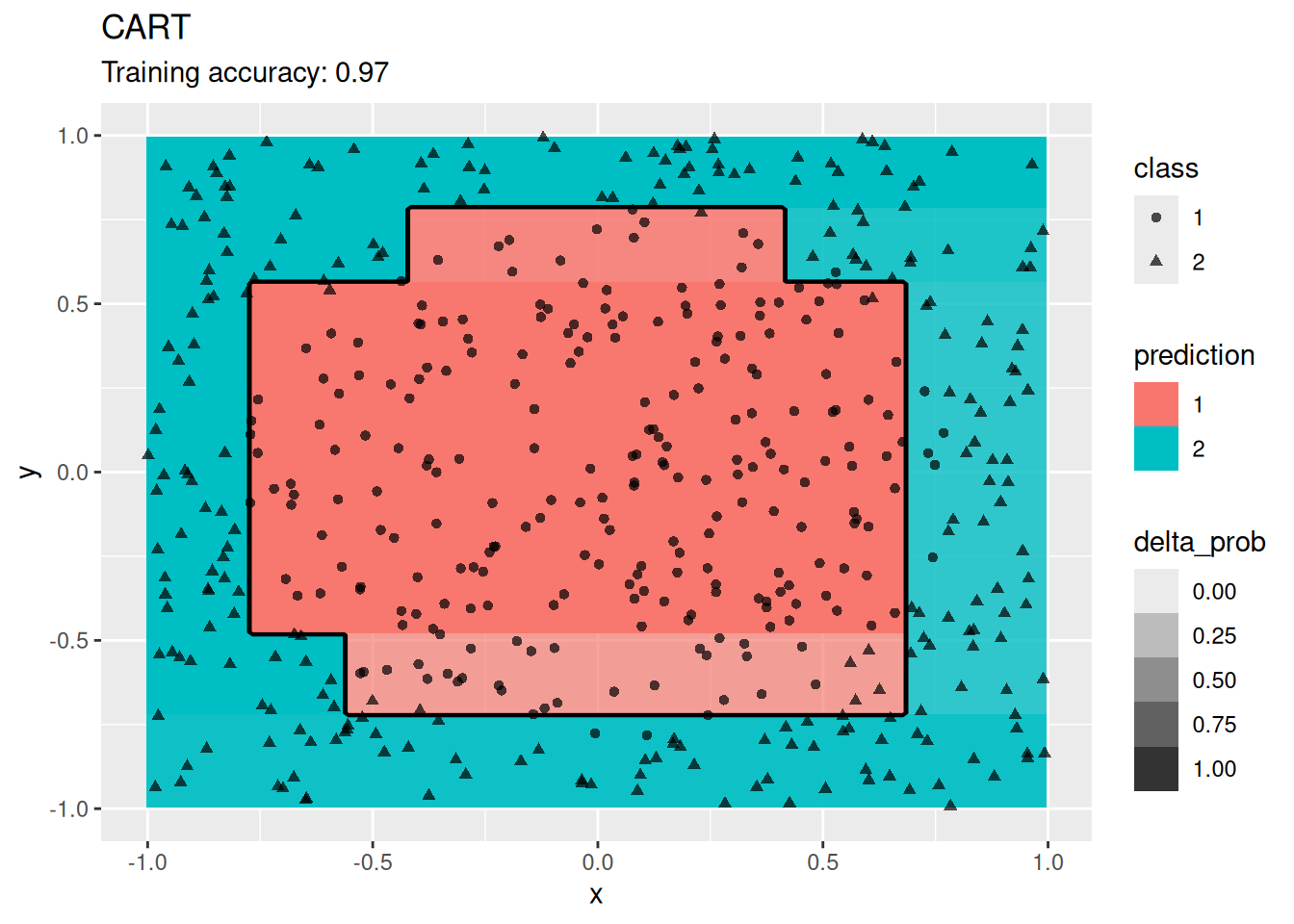
This dataset is challenging for some classification algorithms since the optimal decision boundary is a circle around the class in the center.
4.12.2.1 Nearest Neighbor Classifier
Compare kNN classifiers with different values for \(k\).
model <- x |> caret::knn3(class ~ ., data = _, k = 1)
decisionplot(model, x, class_var = "class") +
labs(title = "kNN (1 neighbor)")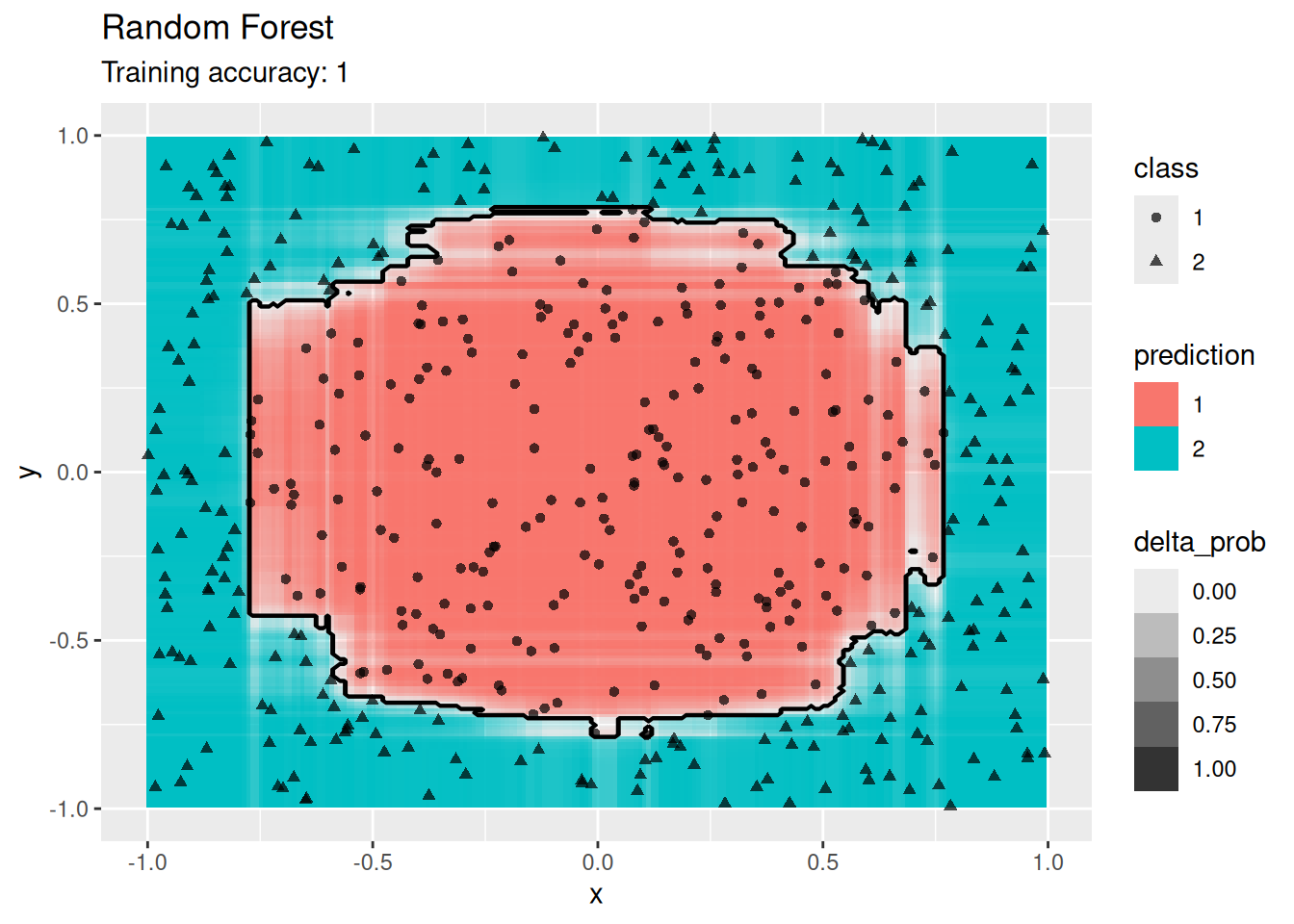
model <- x |> caret::knn3(class ~ ., data = _, k = 10)
decisionplot(model, x, class_var = "class") +
labs(title = "kNN (10 neighbors)")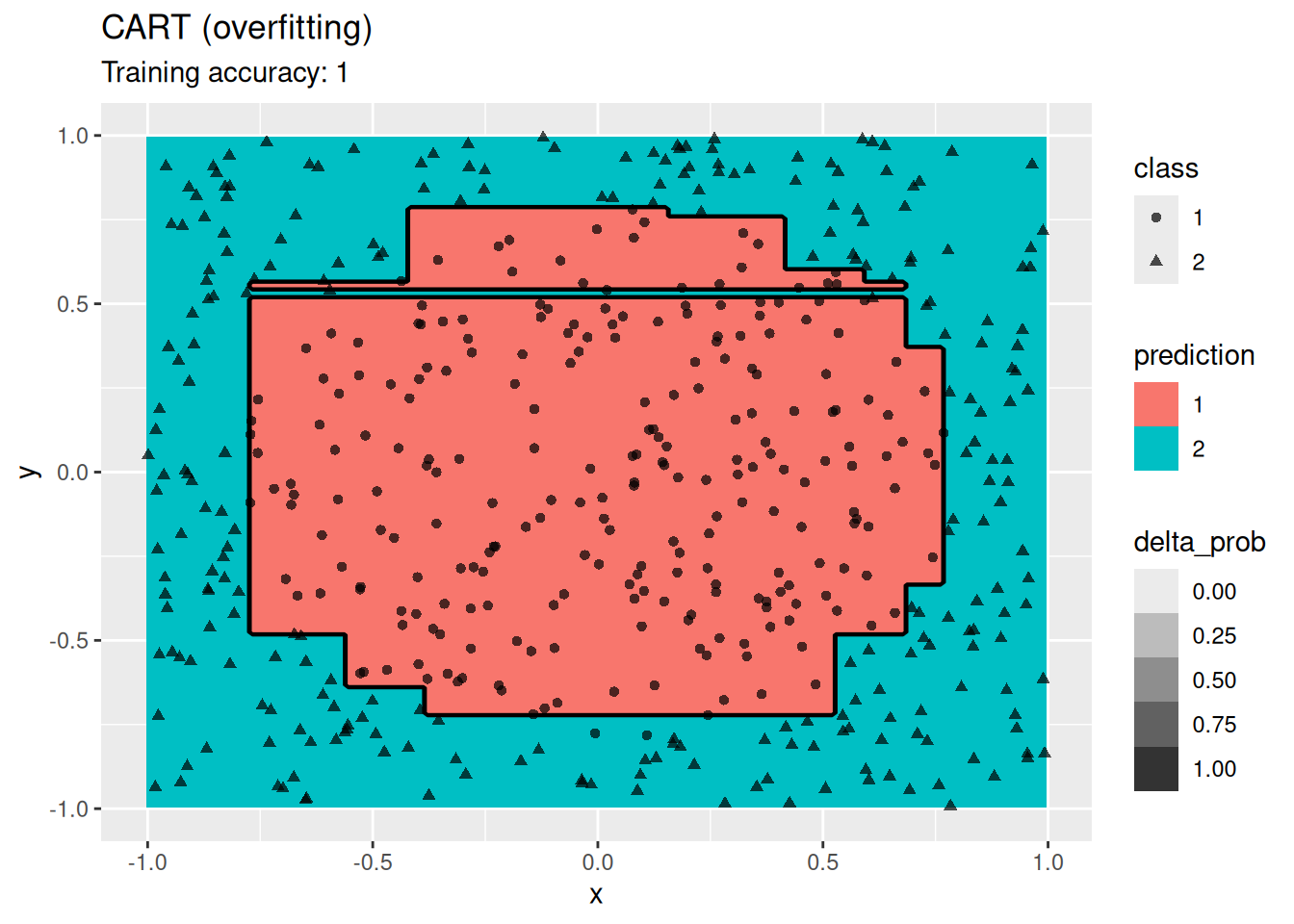
k-Nearest does not find a smooth decision boundary, but tends to overfit the training data at low values for \(k\).
4.12.2.2 Naive Bayes Classifier
The Gaussian naive Bayes classifier works very well on the data.
model <- x |> e1071::naiveBayes(class ~ ., data = _)
decisionplot(model, x, class_var = "class",
predict_type = c("class", "raw")) +
labs(title = "naive Bayes")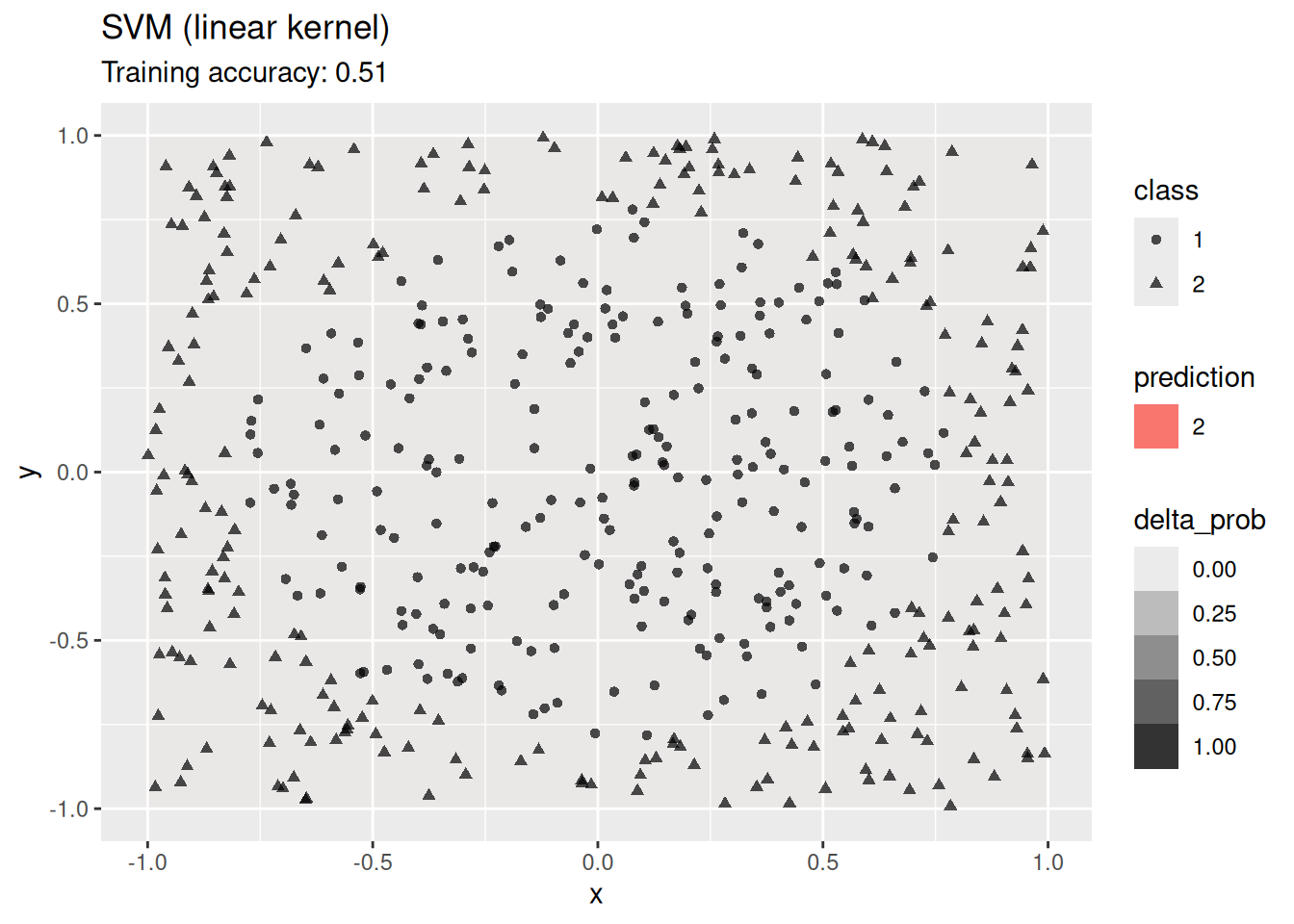
4.12.2.3 Linear Discriminant Analysis
LDA cannot find a good model since the true decision boundary is not linear.
model <- x |> MASS::lda(class ~ ., data = _)
decisionplot(model, x, class_var = "class") + labs(title = "LDA")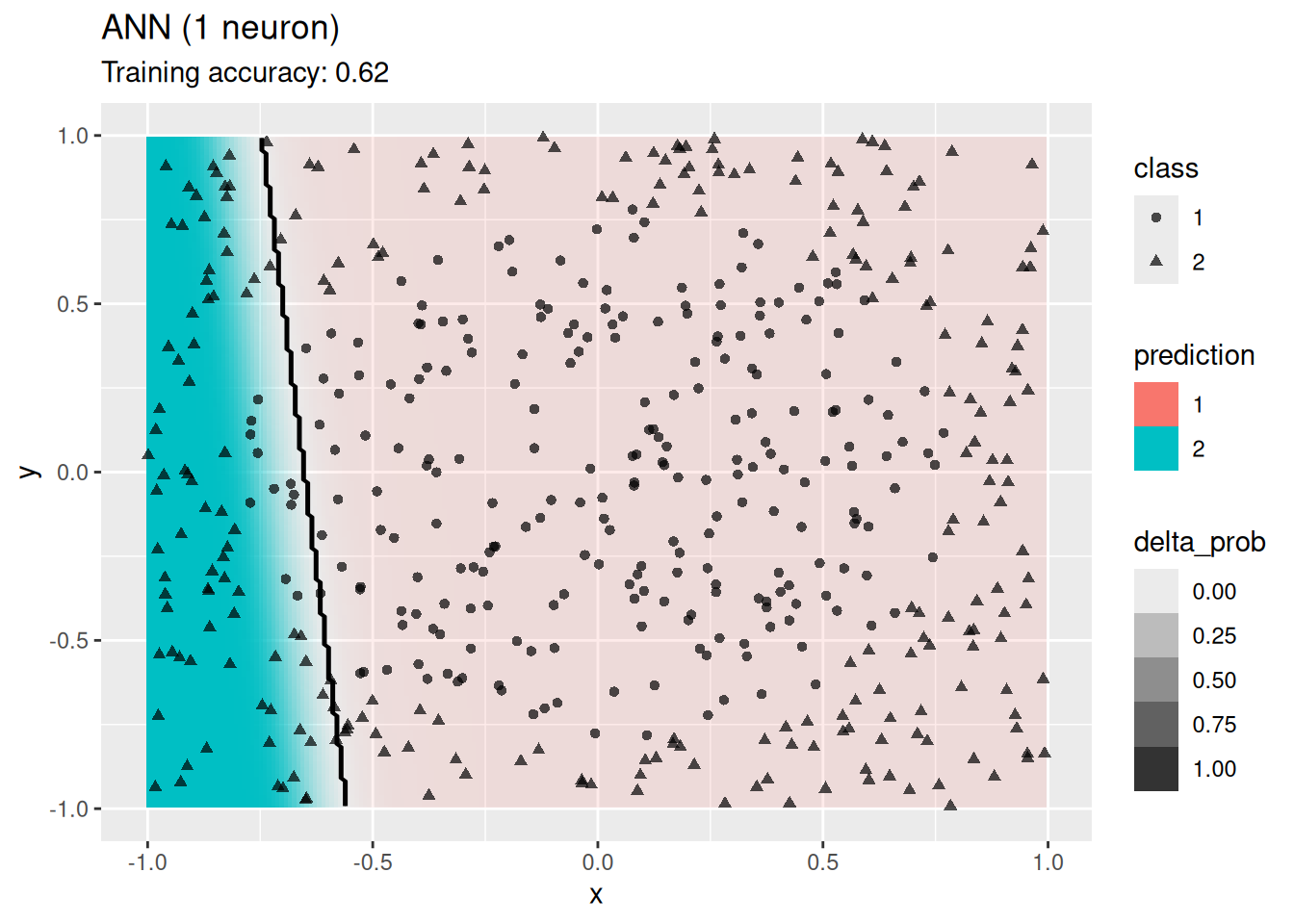
4.12.2.4 Multinomial Logistic Regression
Multinomial logistic regression is an extension of logistic regression to problems with more than two classes.
model <- x |> nnet::multinom(class ~., data = _)
## # weights: 4 (3 variable)
## initial value 346.573590
## final value 346.308371
## converged
decisionplot(model, x, class_var = "class") +
labs(titel = "Multinomial Logistic Regression")
## Ignoring unknown labels:
## • titel : "Multinomial Logistic Regression"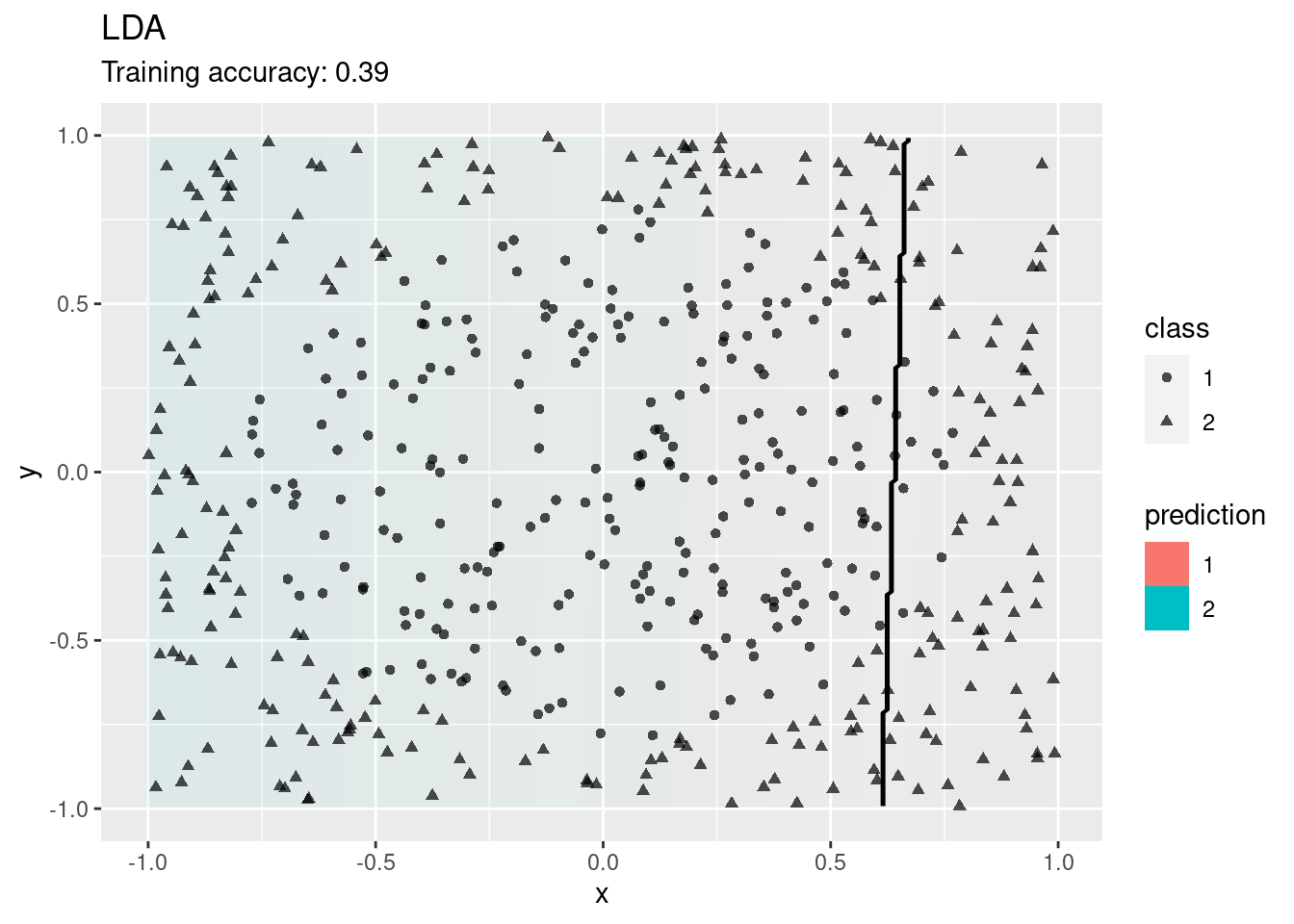
Logistic regression also tries to find a linear decision boundary and fails.
4.12.2.5 Decision Trees
Compare different decision tree algorithms.
model <- x |> rpart::rpart(class ~ ., data = _)
decisionplot(model, x, class_var = "class") +
labs(title = "CART")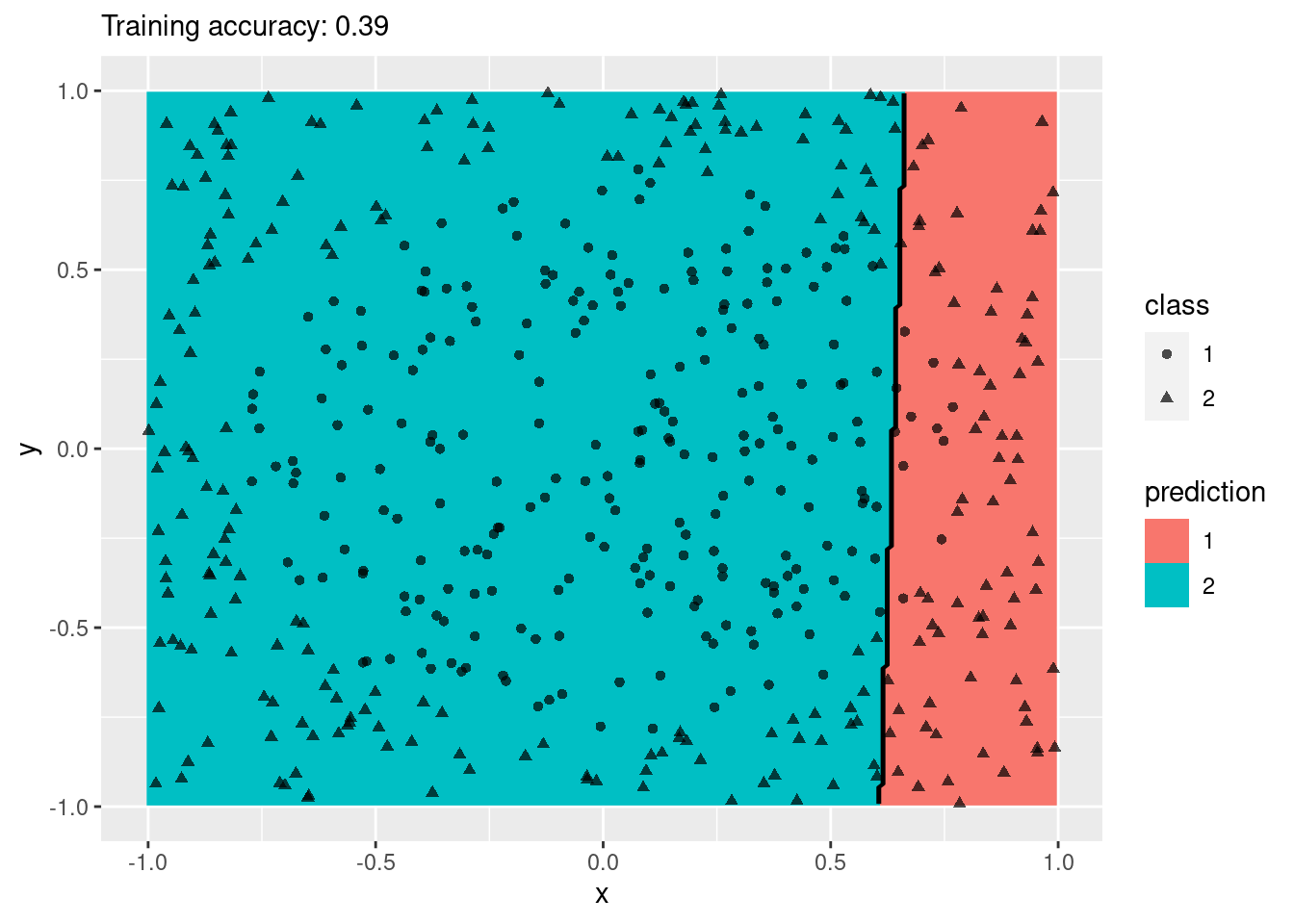
model <- x |> rpart::rpart(class ~ ., data = _,
control = rpart::rpart.control(cp = 0, minsplit = 1))
decisionplot(model, x, class_var = "class") +
labs(title = "CART (overfitting)")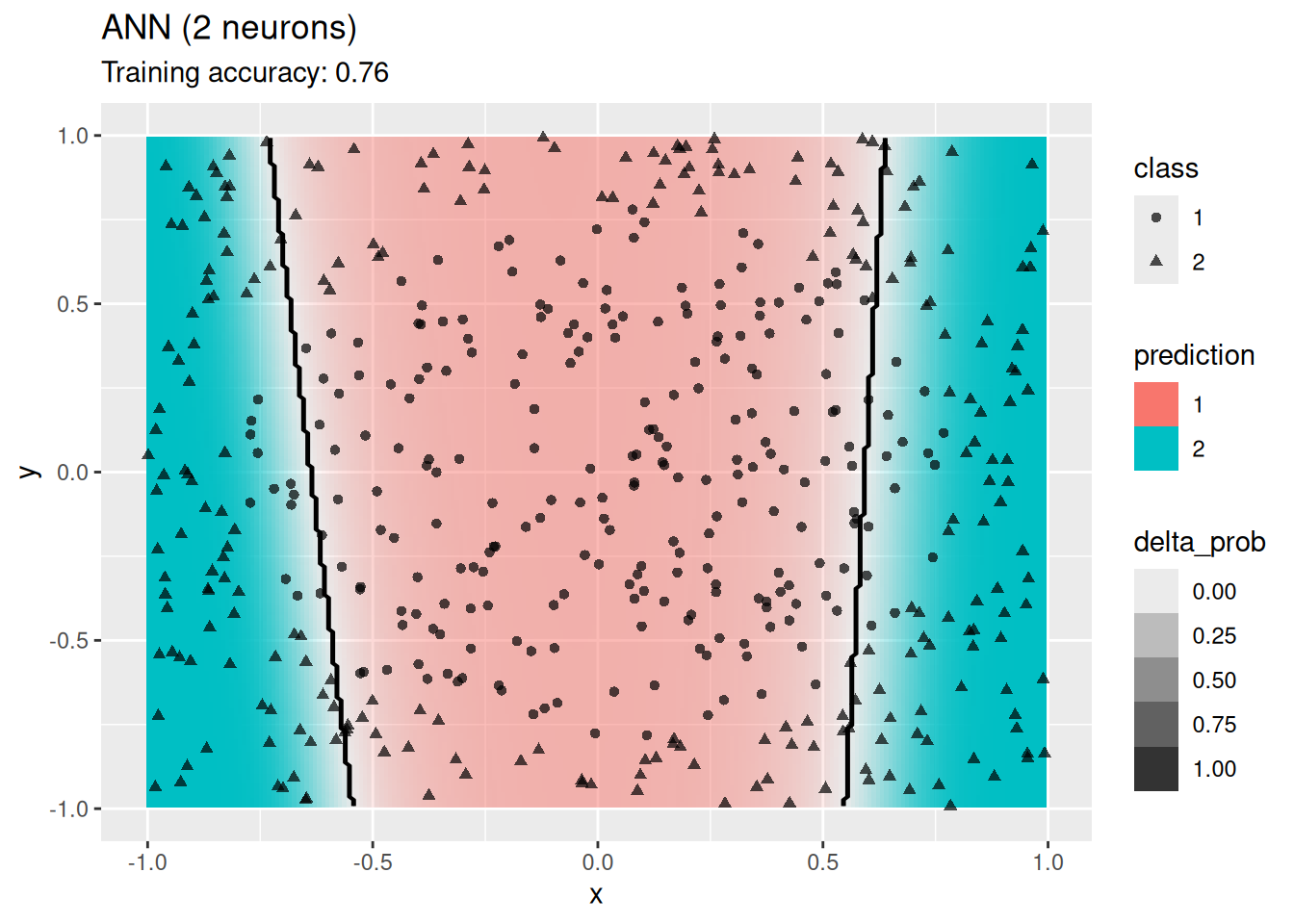
model <- x |> C50::C5.0(class ~ ., data = _)
decisionplot(model, x, class_var = "class") +
labs(title = "C5.0")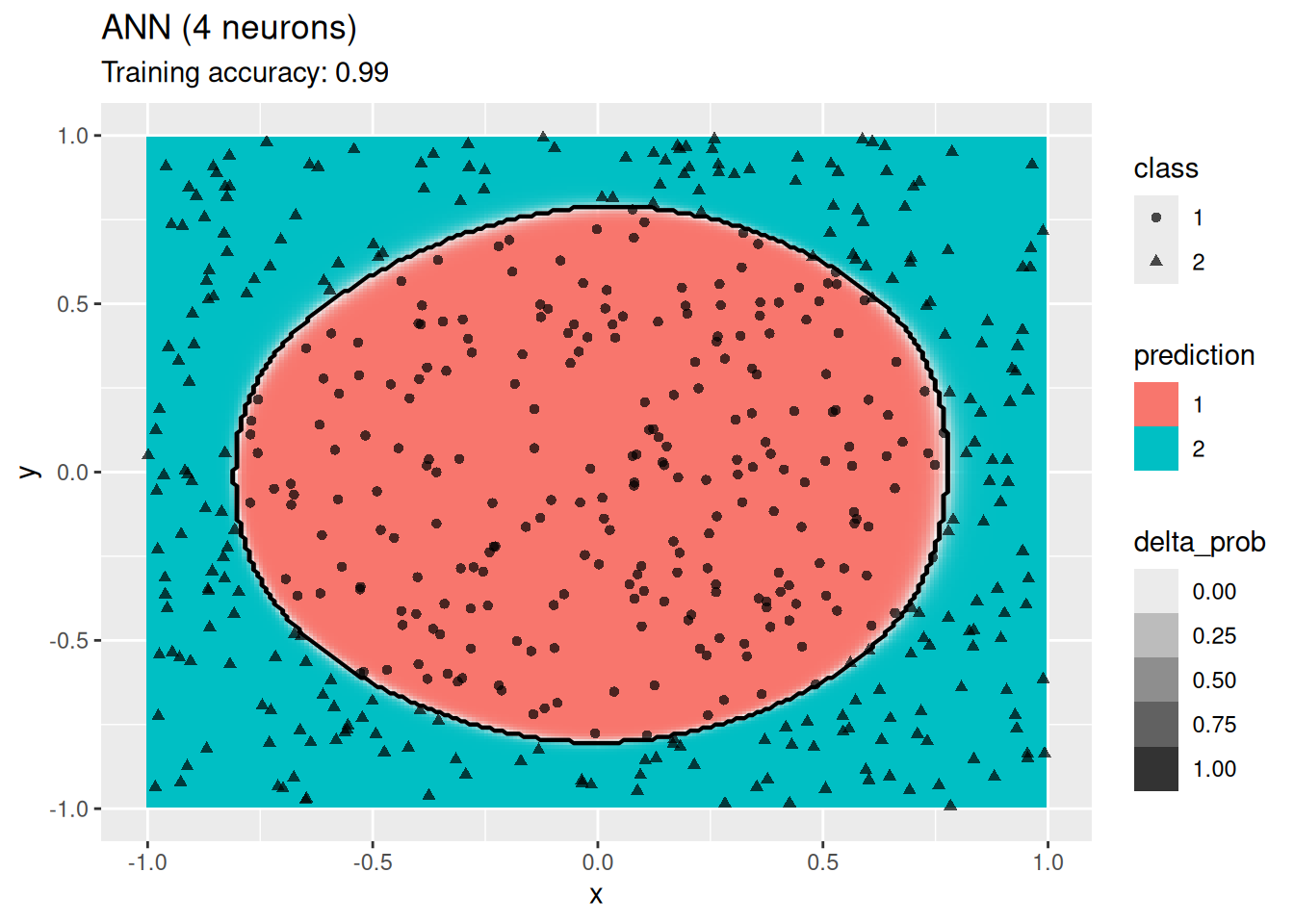
Decision trees do well with the restriction that they can only create cuts parallel to the axes.
4.12.2.6 Ensemble: Random Forest
Try random forest on the dataset.
library(randomForest)
## randomForest 4.7-1.2
## Type rfNews() to see new features/changes/bug fixes.
##
## Attaching package: 'randomForest'
## The following object is masked from 'package:dplyr':
##
## combine
## The following object is masked from 'package:ggplot2':
##
## margin
model <- x |> randomForest(class ~ ., data = _)
decisionplot(model, x, class_var = "class") +
labs(title = "Random Forest")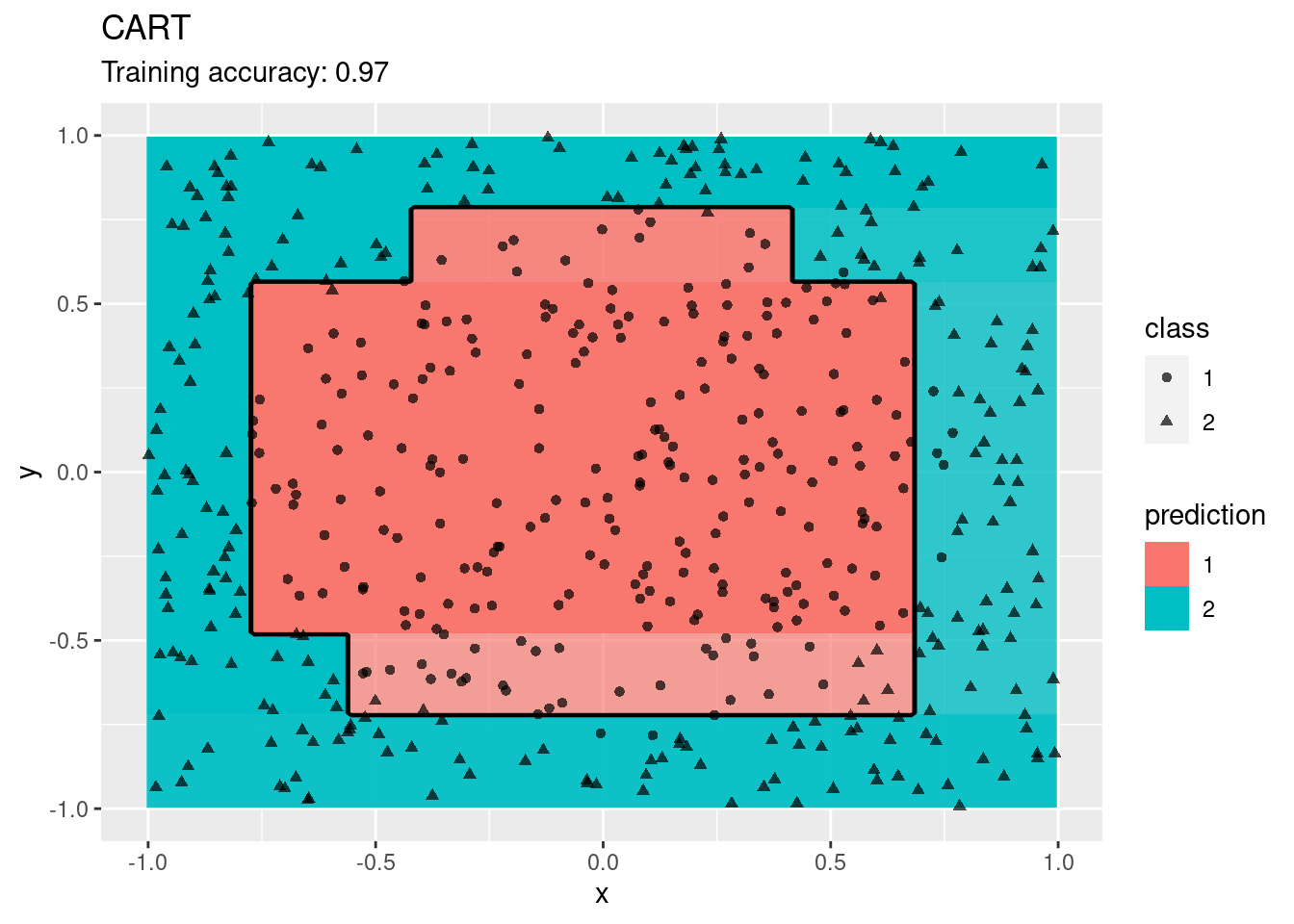
4.12.2.7 Support Vector Machine
Compare SVMs with different kernels.
model <- x |> e1071::svm(class ~ ., data = _,
kernel = "linear", probability = TRUE)
decisionplot(model, x, class_var = "class") +
labs(title = "SVM (linear kernel)")
## Warning: Computation failed in `stat_contour()`.
## Caused by error in `zero_range()`:
## ! `x` must be length 1 or 2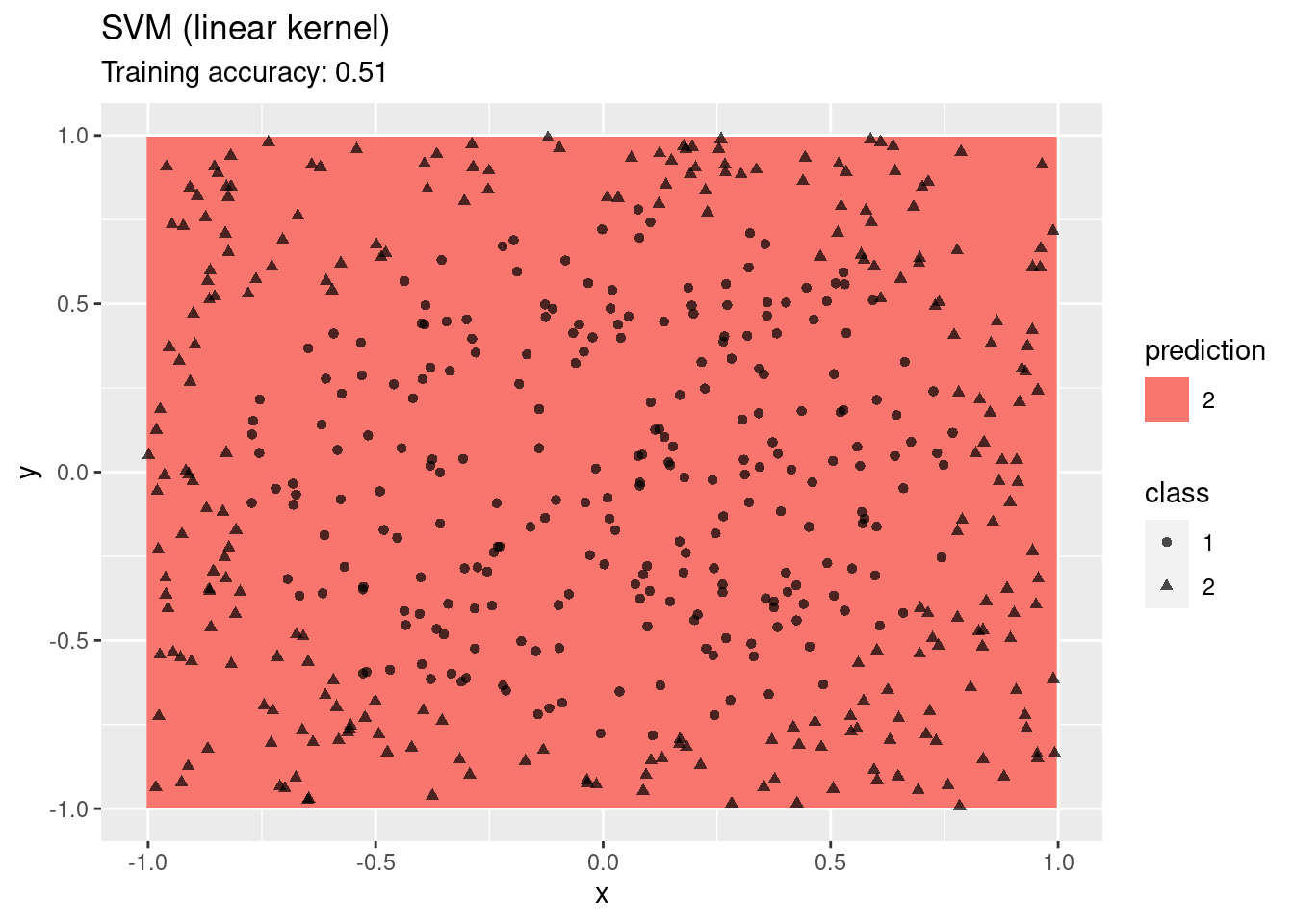
model <- x |> e1071::svm(class ~ ., data = _,
kernel = "radial", probability = TRUE)
decisionplot(model, x, class_var = "class") +
labs(title = "SVM (radial kernel)")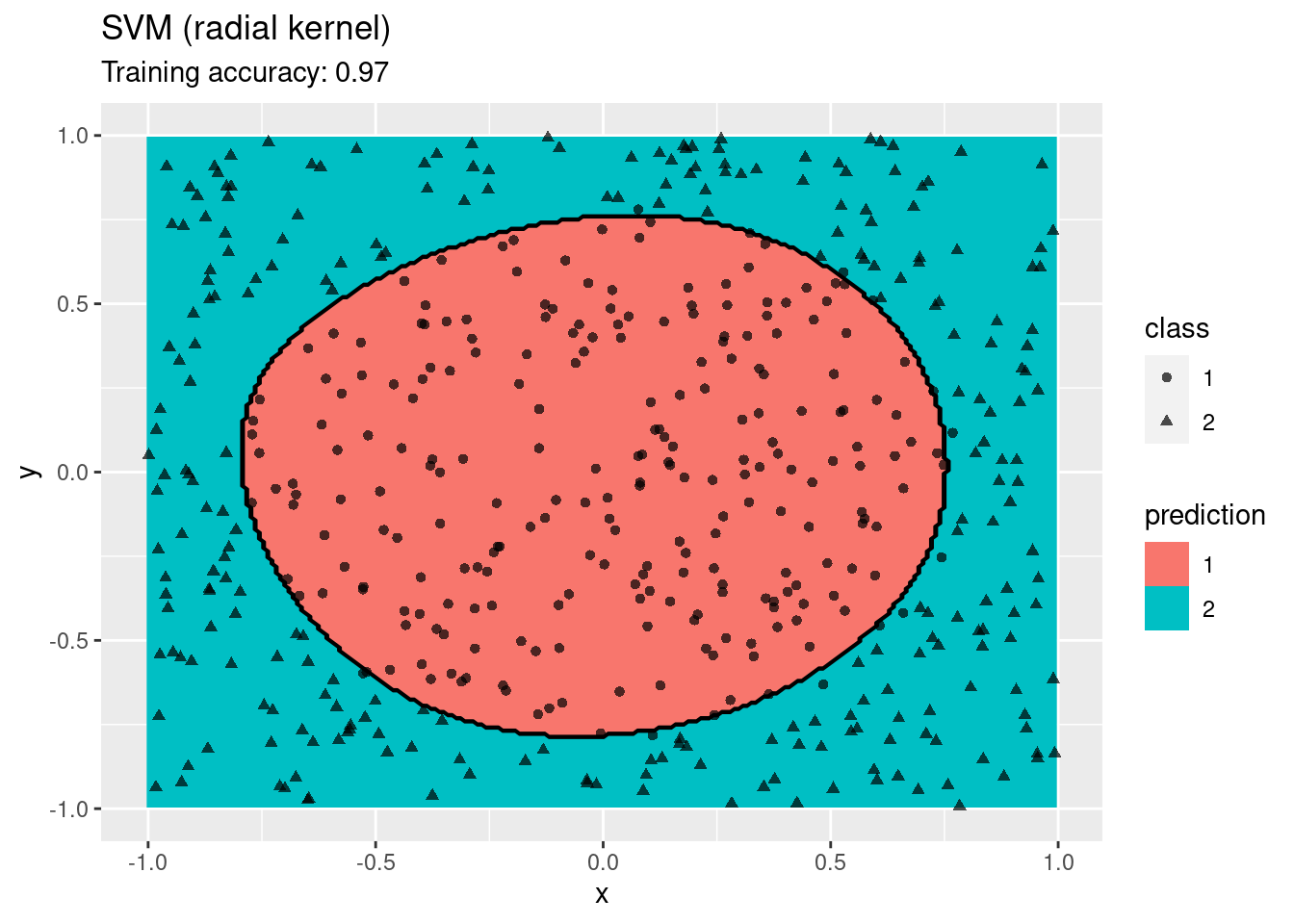
model <- x |> e1071::svm(class ~ ., data = _,
kernel = "polynomial", probability = TRUE)
decisionplot(model, x, class_var = "class") +
labs(title = "SVM (polynomial kernel)")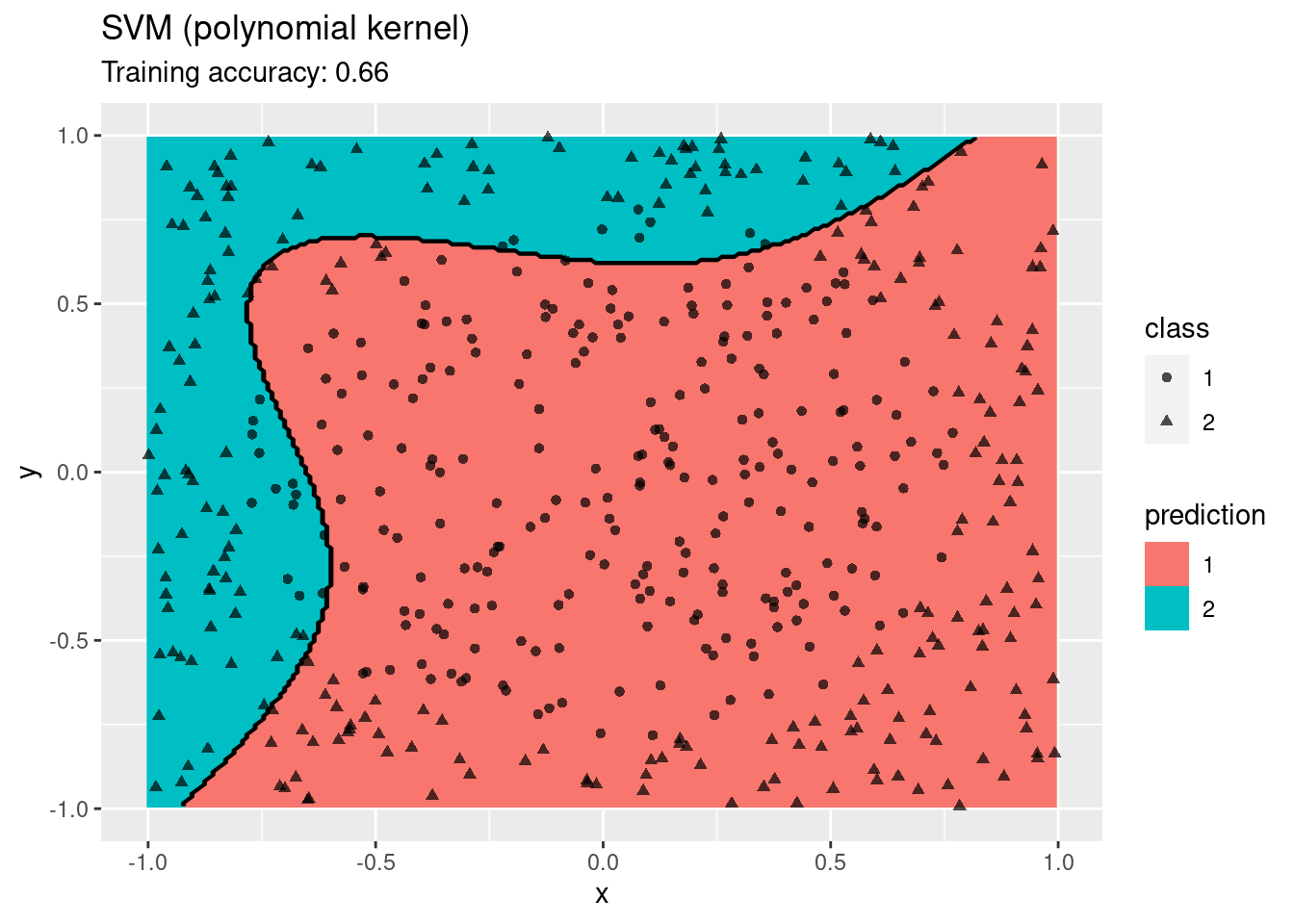
model <- x |> e1071::svm(class ~ ., data = _,
kernel = "sigmoid", probability = TRUE)
decisionplot(model, x, class_var = "class") +
labs(title = "SVM (sigmoid kernel)")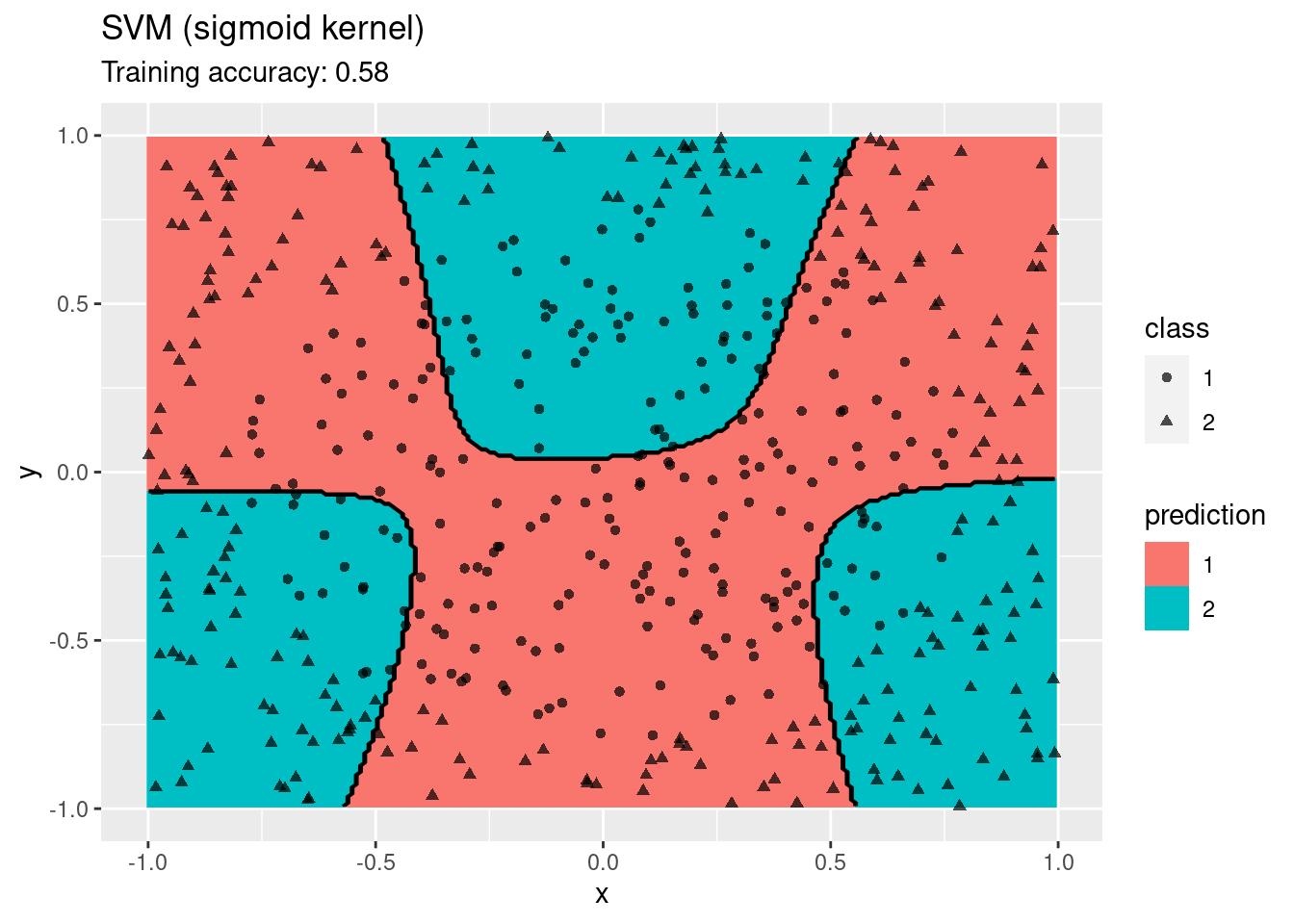
A linear SVM does not work on this data set. An SMV with a radial kernel performs well, the other kernels have issues with finding a linear decision boundary in the projected space.
4.12.2.8 Single Layer Feed-forward Neural Networks
Use a simple network with one hidden layer. We will try a different number of neurons for the hidden layer.
model <- x |> nnet::nnet(class ~ ., data = _, size = 1, trace = FALSE)
decisionplot(model, x, class_var = "class",
predict_type = c("class", "raw")) + labs(title = "ANN (1 neuron)")
model <- x |> nnet::nnet(class ~ ., data = _, size = 2, trace = FALSE)
decisionplot(model, x, class_var = "class",
predict_type = c("class", "raw")) + labs(title = "ANN (2 neurons)")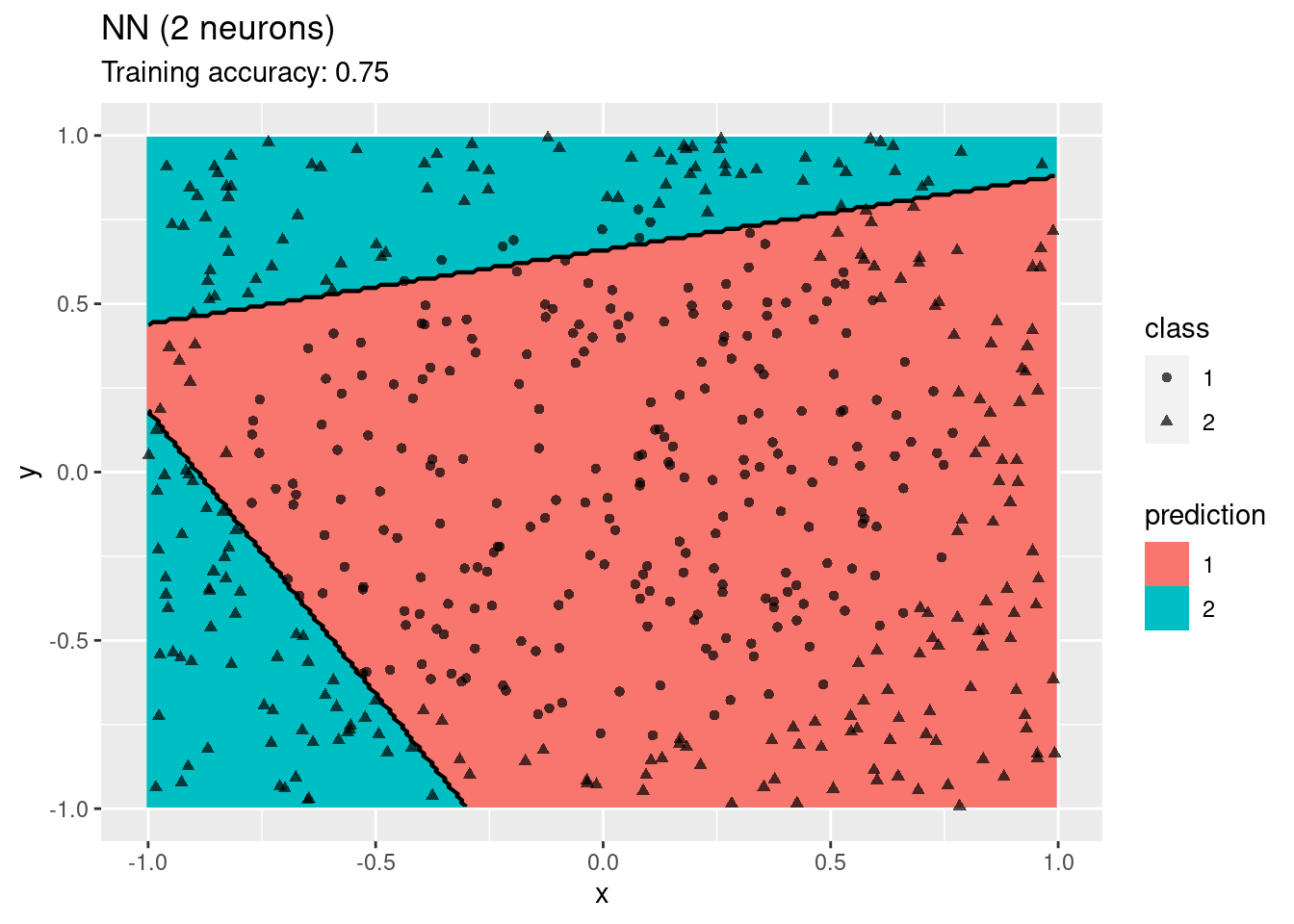
model <- x |> nnet::nnet(class ~ ., data = _, size = 4, trace = FALSE)
decisionplot(model, x, class_var = "class",
predict_type = c("class", "raw")) + labs(title = "ANN (4 neurons)")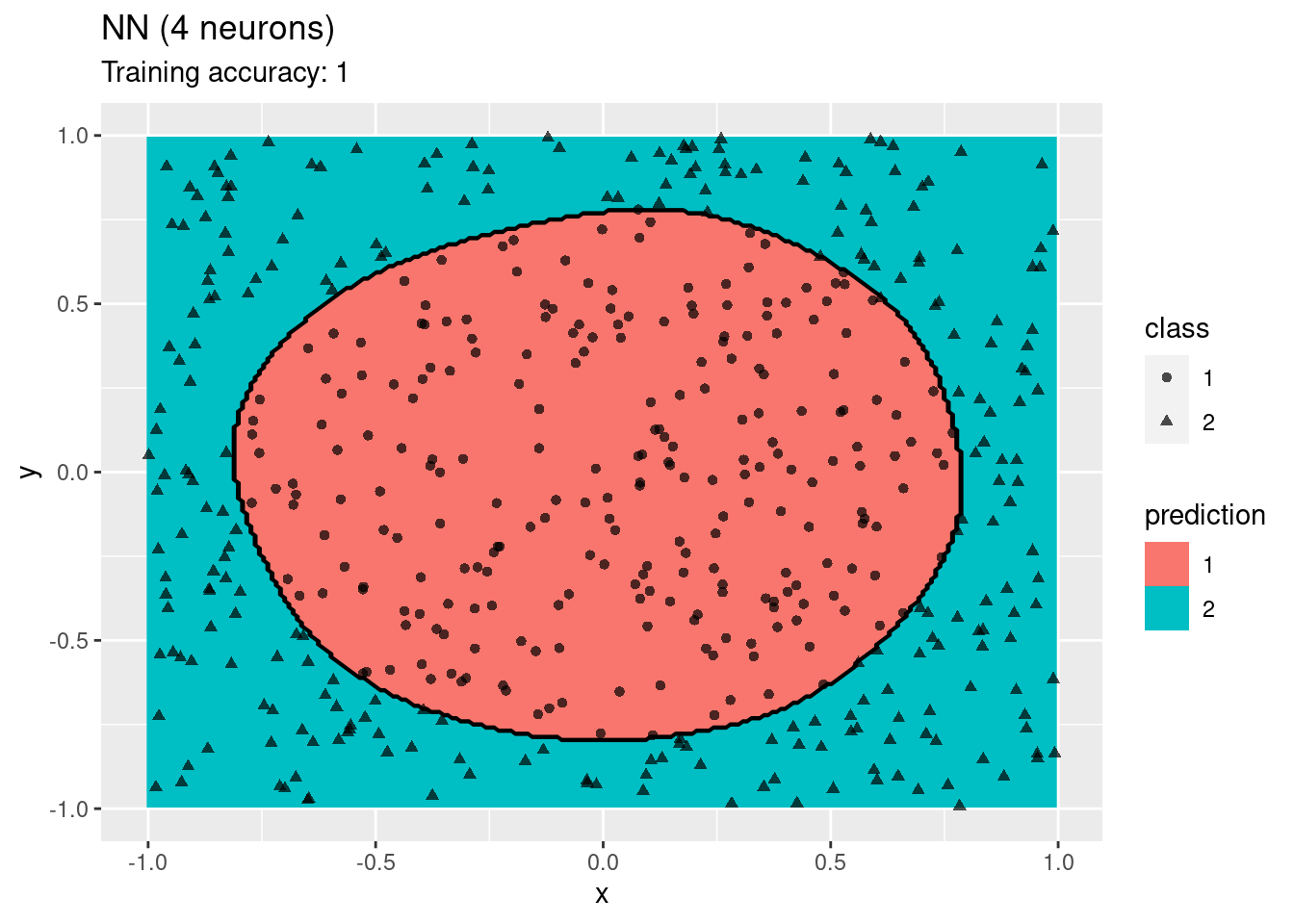
model <- x |> nnet::nnet(class ~ ., data = _, size = 6, trace = FALSE)
decisionplot(model, x, class_var = "class",
predict_type = c("class", "raw")) + labs(title = "ANN (6 neurons)")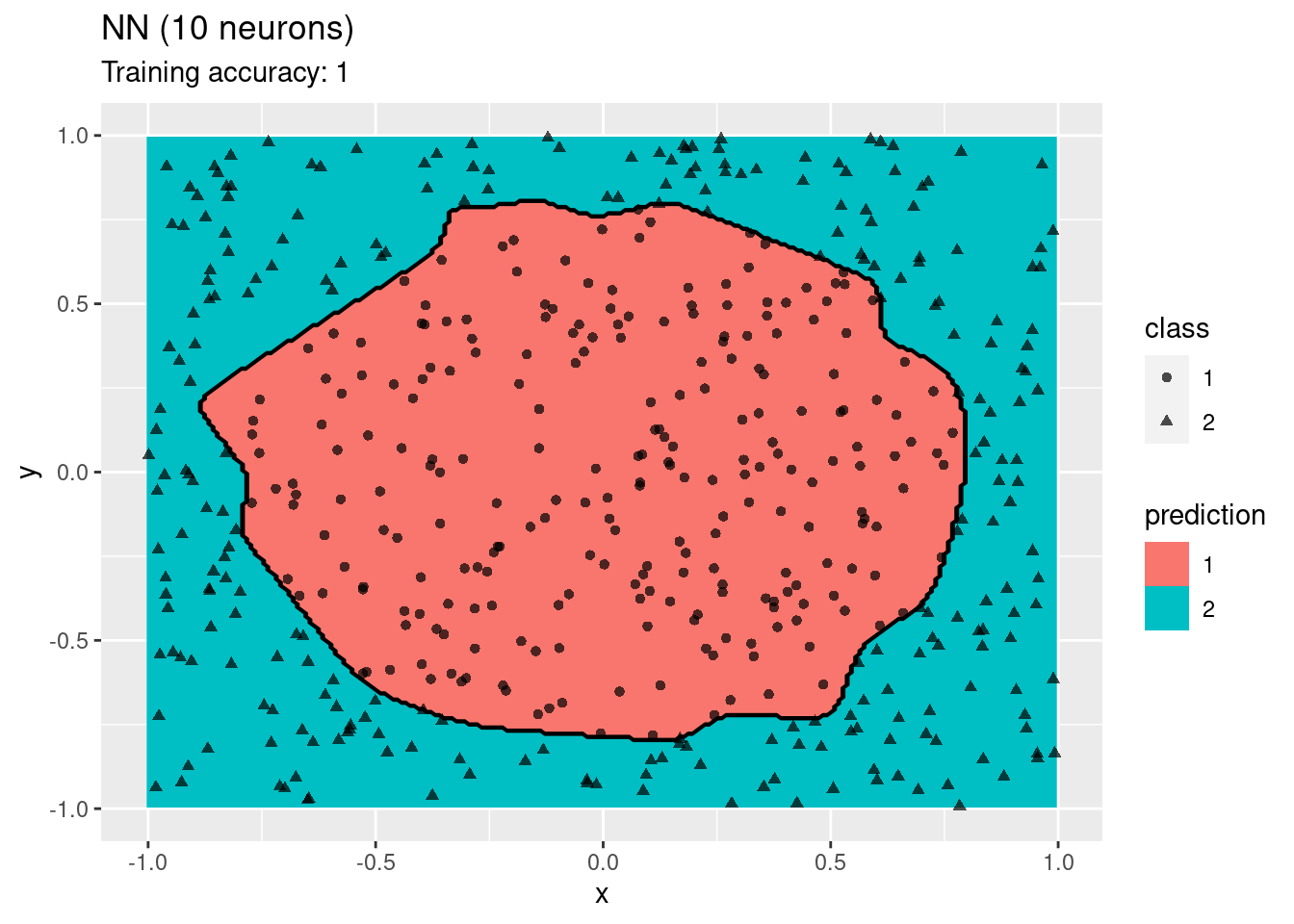
model <- x |> nnet::nnet(class ~ ., data = _, size = 20, trace = FALSE)
decisionplot(model, x, class_var = "class",
predict_type = c("class", "raw")) + labs(title = "ANN (20 neurons)")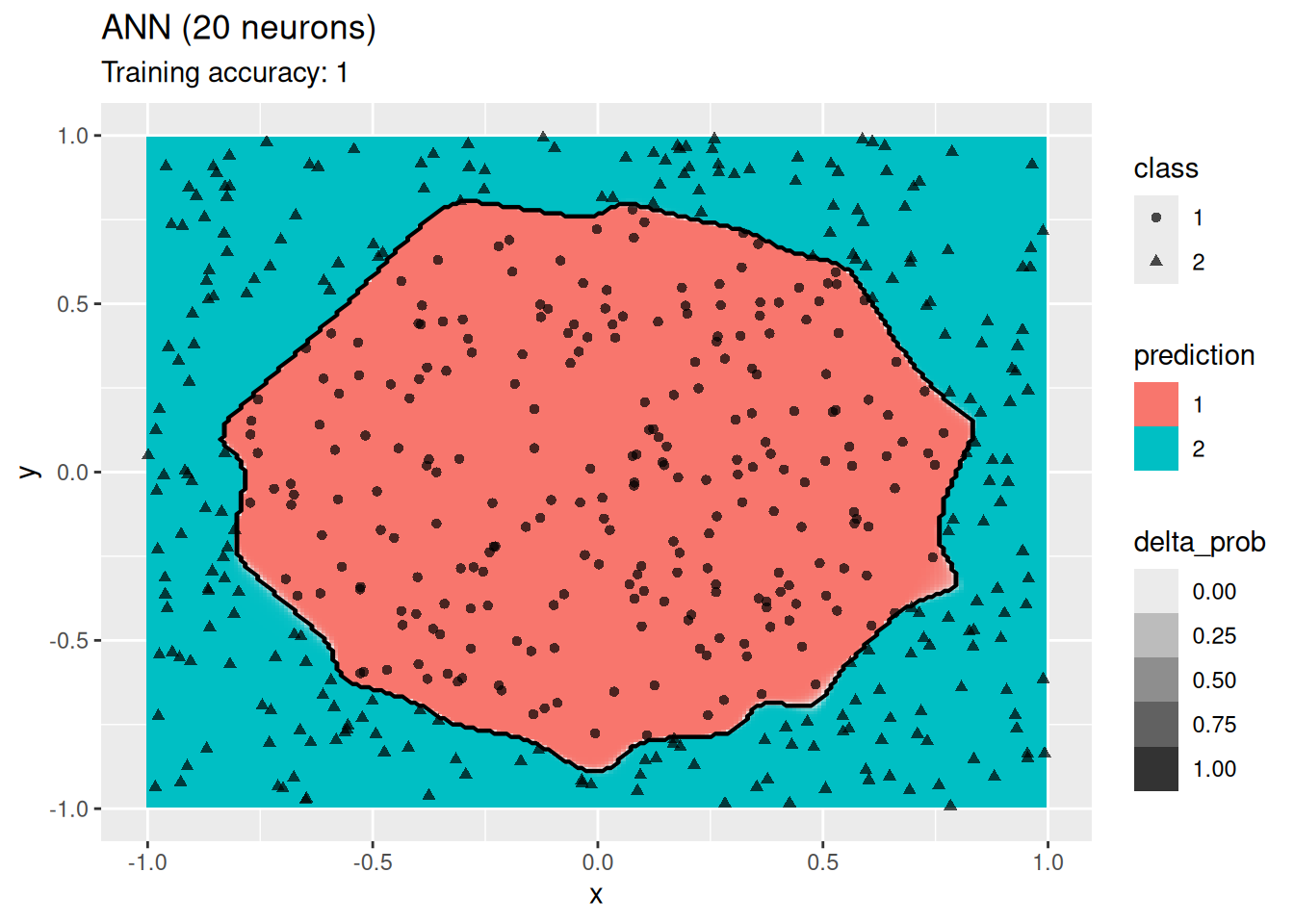
The plots show that a network with 4 and 6 neurons performs well, while a larger number of neurons leads to overfitting the training data.
4.13 More Information on Classification with R
- Package caret: http://topepo.github.io/caret/index.html
- Tidymodels (machine learning with tidyverse): https://www.tidymodels.org/
- R taskview on machine learning: http://cran.r-project.org/web/views/MachineLearning.html
4.14 Exercises*
We will again use the Palmer penguin data for the exercises.
library(palmerpenguins)
head(penguins)
## # A tibble: 6 × 8
## species island bill_length_mm bill_depth_mm
## <chr> <chr> <dbl> <dbl>
## 1 Adelie Torgersen 39.1 18.7
## 2 Adelie Torgersen 39.5 17.4
## 3 Adelie Torgersen 40.3 18
## 4 Adelie Torgersen NA NA
## 5 Adelie Torgersen 36.7 19.3
## 6 Adelie Torgersen 39.3 20.6
## # ℹ 4 more variables: flipper_length_mm <dbl>,
## # body_mass_g <dbl>, sex <chr>, year <dbl>Create a R markdown file with the code and do the following below.
- Apply at least 3 different classification models to the data.
- Compare the models and a simple baseline model. Which model performs the best? Does it perform significantly better than the other models?