5 Association Analysis: Basic Concepts
This chapter introduces association rules mining using the APRIORI algorithm. In addition, analyzing sets of association rules using visualization techniques is demonstrated.
The corresponding chapter of the data mining textbook is available online: Chapter 5: Association Analysis: Basic Concepts and Algorithms.
Packages Used in this Chapter
pkgs <- c("arules", "arulesViz", "mlbench",
"palmerpenguins", "tidyverse")
pkgs_install <- pkgs[!(pkgs %in% installed.packages()[,"Package"])]
if(length(pkgs_install)) install.packages(pkgs_install)The packages used for this chapter are:
- arules (Hahsler et al. 2025)
- arulesViz (Hahsler 2025)
- mlbench (Leisch and Dimitriadou 2024)
- palmerpenguins (Horst, Hill, and Gorman 2022)
- tidyverse (Wickham 2023b)
5.1 Preliminaries
Association rule mining plays a vital role in discovering hidden patterns and relationships within large transactional datasets. Applications range from exploratory data analysis in marketing to building rule-based classifiers. Agrawal, Imielinski, and Swami (1993) introduced the problem of mining association rules from transaction data as follows (the definition is taken from Hahsler, Grün, and Hornik (2005)):
Let \(I = \{i_1,i_2,...,i_n\}\) be a set of \(n\) binary attributes called items. Let \(D = \{t_1,t_2,...,t_m\}\) be a set of transactions called the database. Each transaction in \(D\) has a unique transaction ID and contains a subset of the items in \(I\). A rule is defined as an implication of the form \(X \Rightarrow Y\) where \(X,Y \subseteq I\) and \(X \cap Y = \emptyset\) are called itemsets. On itemsets and rules several quality measures can be defined. The most important measures are support and confidence. The support \(supp(X)\) of an itemset \(X\) is defined as the proportion of transactions in the data set which contain the itemset. Itemsets with a support which surpasses a user-defined threshold \(\sigma\) are called frequent itemsets. The confidence of a rule is defined as \(conf(X \Rightarrow Y) = supp(X \cup Y)/supp(X)\). Association rules are rules with \(supp(X \cup Y) \ge \sigma\) and \(conf(X) \ge \delta\) where \(\sigma\) and \(\delta\) are user-defined thresholds. The found set of association rules is then used reason about the data.
You can read the free sample chapter from the textbook (Tan, Steinbach, and Kumar 2005): Chapter 5. Association Analysis: Basic Concepts and Algorithms
5.1.1 The arules Package
Association rule mining in R is implemented in the package arules.
For information about the arules package try: help(package="arules")
and vignette("arules") (also available at
CRAN)
arules uses the S4 object system to implement classes and methods.
Standard R objects use the S3 object
system which do not use formal class
definitions and are usually implemented as a list with a class
attribute. arules and many other R packages use the S4 object
system which is based on formal class
definitions with member variables and methods (similar to
object-oriented programming languages like Java and C++). Some important
differences of using S4 objects compared to the usual S3 objects are:
- coercion (casting):
as(from, "class_name") - help for classes:
class? class_name
5.1.2 Transactions
5.1.2.1 Create Transactions
We will use the Zoo dataset from mlbench.
data(Zoo, package = "mlbench")
head(Zoo)
## hair feathers eggs milk airborne aquatic
## aardvark TRUE FALSE FALSE TRUE FALSE FALSE
## antelope TRUE FALSE FALSE TRUE FALSE FALSE
## bass FALSE FALSE TRUE FALSE FALSE TRUE
## bear TRUE FALSE FALSE TRUE FALSE FALSE
## boar TRUE FALSE FALSE TRUE FALSE FALSE
## buffalo TRUE FALSE FALSE TRUE FALSE FALSE
## predator toothed backbone breathes venomous fins
## aardvark TRUE TRUE TRUE TRUE FALSE FALSE
## antelope FALSE TRUE TRUE TRUE FALSE FALSE
## bass TRUE TRUE TRUE FALSE FALSE TRUE
## bear TRUE TRUE TRUE TRUE FALSE FALSE
## boar TRUE TRUE TRUE TRUE FALSE FALSE
## buffalo FALSE TRUE TRUE TRUE FALSE FALSE
## legs tail domestic catsize type
## aardvark 4 FALSE FALSE TRUE mammal
## antelope 4 TRUE FALSE TRUE mammal
## bass 0 TRUE FALSE FALSE fish
## bear 4 FALSE FALSE TRUE mammal
## boar 4 TRUE FALSE TRUE mammal
## buffalo 4 TRUE FALSE TRUE mammalThe data in the data.frame need to be converted into a set of
transactions where each row represents a transaction and each column is
translated into items. This is done using the constructor
transactions(). For the Zoo data set this means that we consider
animals as transactions and the different traits (features) will become
items that each animal has. For example the animal antelope has the
item hair in its transaction.
trans <- transactions(Zoo)
## Warning: Column(s) 13 not logical or factor. Applying
## default discretization (see '? discretizeDF').The conversion gives a warning because only discrete features (factor
and logical) can be directly translated into items. Continuous
features need to be discretized first.
What is column 13?
summary(Zoo[13])
## legs
## Min. :0.00
## 1st Qu.:2.00
## Median :4.00
## Mean :2.84
## 3rd Qu.:4.00
## Max. :8.00
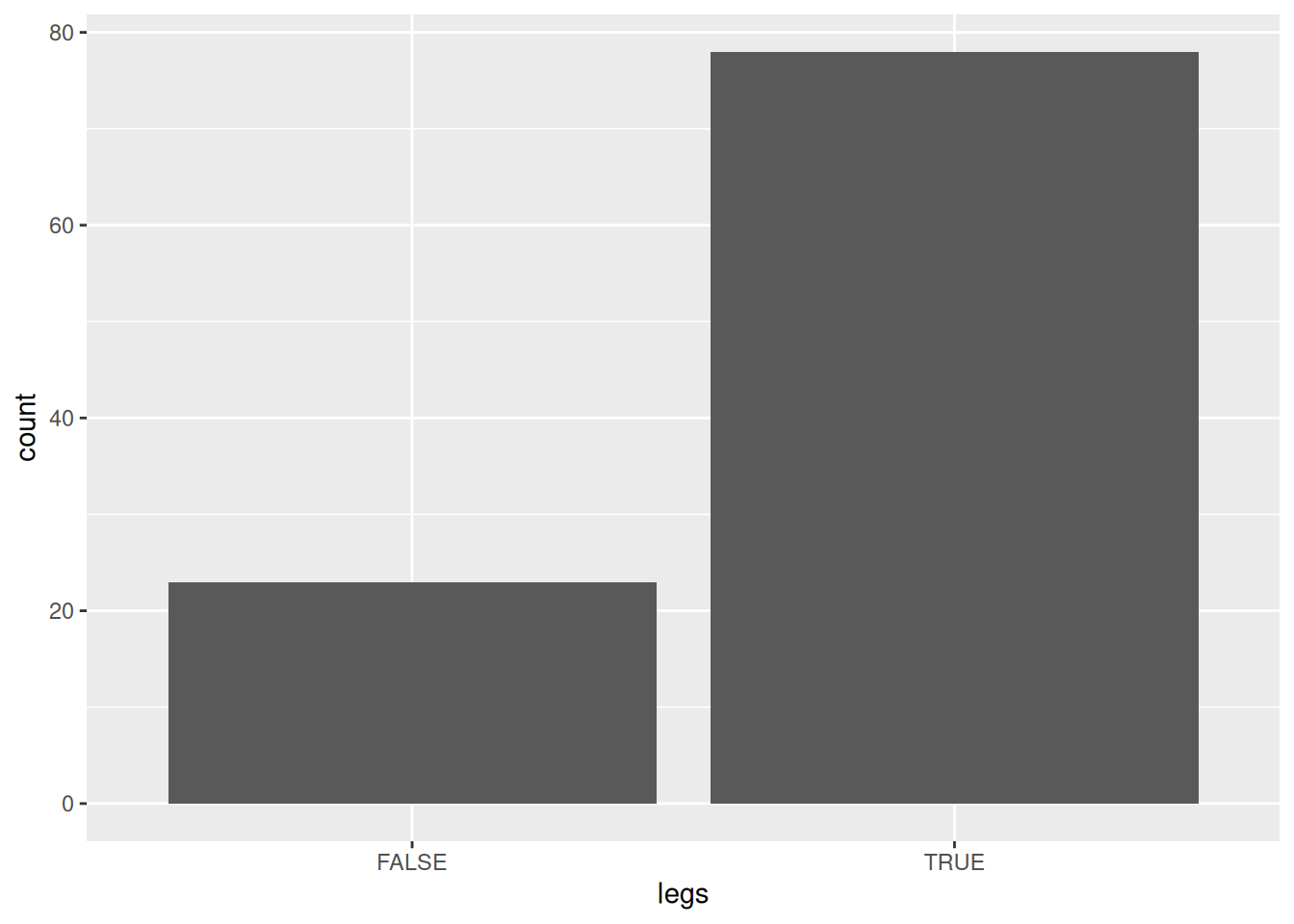
ggplot(Zoo, aes(legs)) + geom_bar()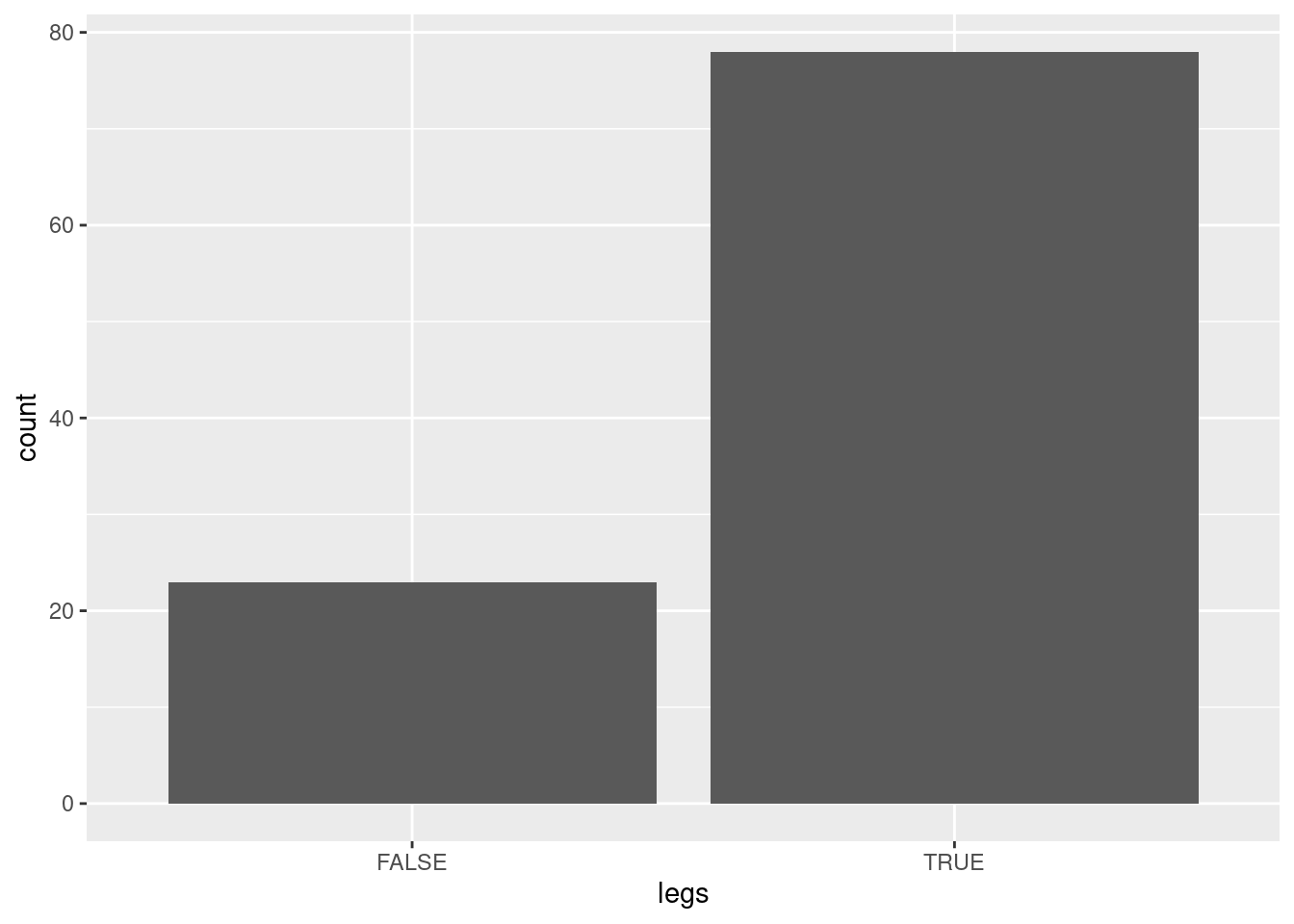
Zoo$legs |> table()
##
## 0 2 4 5 6 8
## 23 27 38 1 10 2There are several ways how we can convert a continuous value into discrete items
5.1.2.2 Alternative Encodings for Continuous Values
Alternative 1: Make legs into has/does not have legs
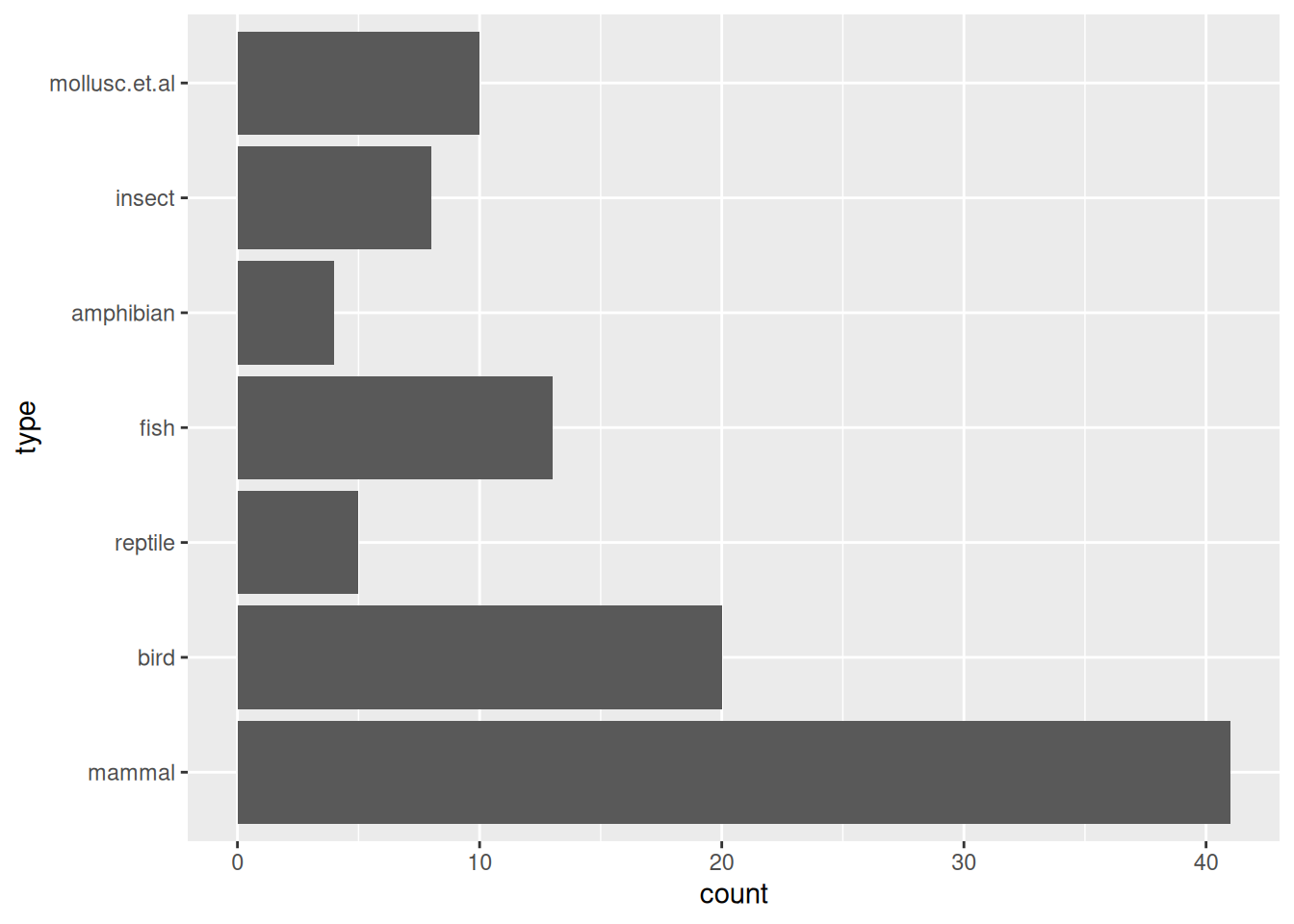
Zoo_has_legs$legs |> table()
##
## FALSE TRUE
## 23 78Alternative 2: Use each unique value as an item.
Zoo_unique_leg_values <- Zoo |> mutate(legs = factor(legs))
Zoo_unique_leg_values$legs |> head()
## [1] 4 4 0 4 4 4
## Levels: 0 2 4 5 6 8Alternative 3: Use the discretize function (see
? discretize
and discretization in the code for Chapter
2):
Zoo_discretized_legs <- Zoo |> mutate(
legs = discretize(legs, breaks = 2, method="interval")
)
table(Zoo_discretized_legs$legs)
##
## [0,4) [4,8]
## 50 51In the following we will use Alternative 1 where the legs item indicates if the animal has legs. We convert this data set into a set of transactions.
trans <- transactions(Zoo_has_legs)
trans
## transactions in sparse format with
## 101 transactions (rows) and
## 23 items (columns)5.1.2.3 Inspecting Transactions
It is very important to check that the conversion to transactions worked as intended.
summary(trans)
## transactions as itemMatrix in sparse format with
## 101 rows (elements/itemsets/transactions) and
## 23 columns (items) and a density of 0.3612
##
## most frequent items:
## backbone breathes legs tail toothed (Other)
## 83 80 78 75 61 462
##
## element (itemset/transaction) length distribution:
## sizes
## 3 4 5 6 7 8 9 10 11 12
## 3 2 6 5 8 21 27 25 3 1
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 3.00 8.00 9.00 8.31 10.00 12.00
##
## includes extended item information - examples:
## labels variables levels
## 1 hair hair TRUE
## 2 feathers feathers TRUE
## 3 eggs eggs TRUE
##
## includes extended transaction information - examples:
## transactionID
## 1 aardvark
## 2 antelope
## 3 bassLook at the created items. They are also called columns names since the transactions are stored as a large, sparse logical matrix.
colnames(trans)
## [1] "hair" "feathers"
## [3] "eggs" "milk"
## [5] "airborne" "aquatic"
## [7] "predator" "toothed"
## [9] "backbone" "breathes"
## [11] "venomous" "fins"
## [13] "legs" "tail"
## [15] "domestic" "catsize"
## [17] "type=mammal" "type=bird"
## [19] "type=reptile" "type=fish"
## [21] "type=amphibian" "type=insect"
## [23] "type=mollusc.et.al"Compare this to the original features (column names) from Zoo.
colnames(Zoo)
## [1] "hair" "feathers" "eggs" "milk" "airborne"
## [6] "aquatic" "predator" "toothed" "backbone" "breathes"
## [11] "venomous" "fins" "legs" "tail" "domestic"
## [16] "catsize" "type"We see that the nominal variable type was converted into several items, one for each value.
We can also look at a (first) few transactions as a logical matrix. TRUE
indicates the presence of an item.
as(trans, "matrix")[1:3,]
## hair feathers eggs milk airborne aquatic
## aardvark TRUE FALSE FALSE TRUE FALSE FALSE
## antelope TRUE FALSE FALSE TRUE FALSE FALSE
## bass FALSE FALSE TRUE FALSE FALSE TRUE
## predator toothed backbone breathes venomous fins
## aardvark TRUE TRUE TRUE TRUE FALSE FALSE
## antelope FALSE TRUE TRUE TRUE FALSE FALSE
## bass TRUE TRUE TRUE FALSE FALSE TRUE
## legs tail domestic catsize type=mammal type=bird
## aardvark TRUE FALSE FALSE TRUE TRUE FALSE
## antelope TRUE TRUE FALSE TRUE TRUE FALSE
## bass FALSE TRUE FALSE FALSE FALSE FALSE
## type=reptile type=fish type=amphibian type=insect
## aardvark FALSE FALSE FALSE FALSE
## antelope FALSE FALSE FALSE FALSE
## bass FALSE TRUE FALSE FALSE
## type=mollusc.et.al
## aardvark FALSE
## antelope FALSE
## bass FALSEThe matrix is large. We can get a visual impression by plot the binary matrix
as an image. Dark dots represent items (TRUE values in the matrix).
image(trans)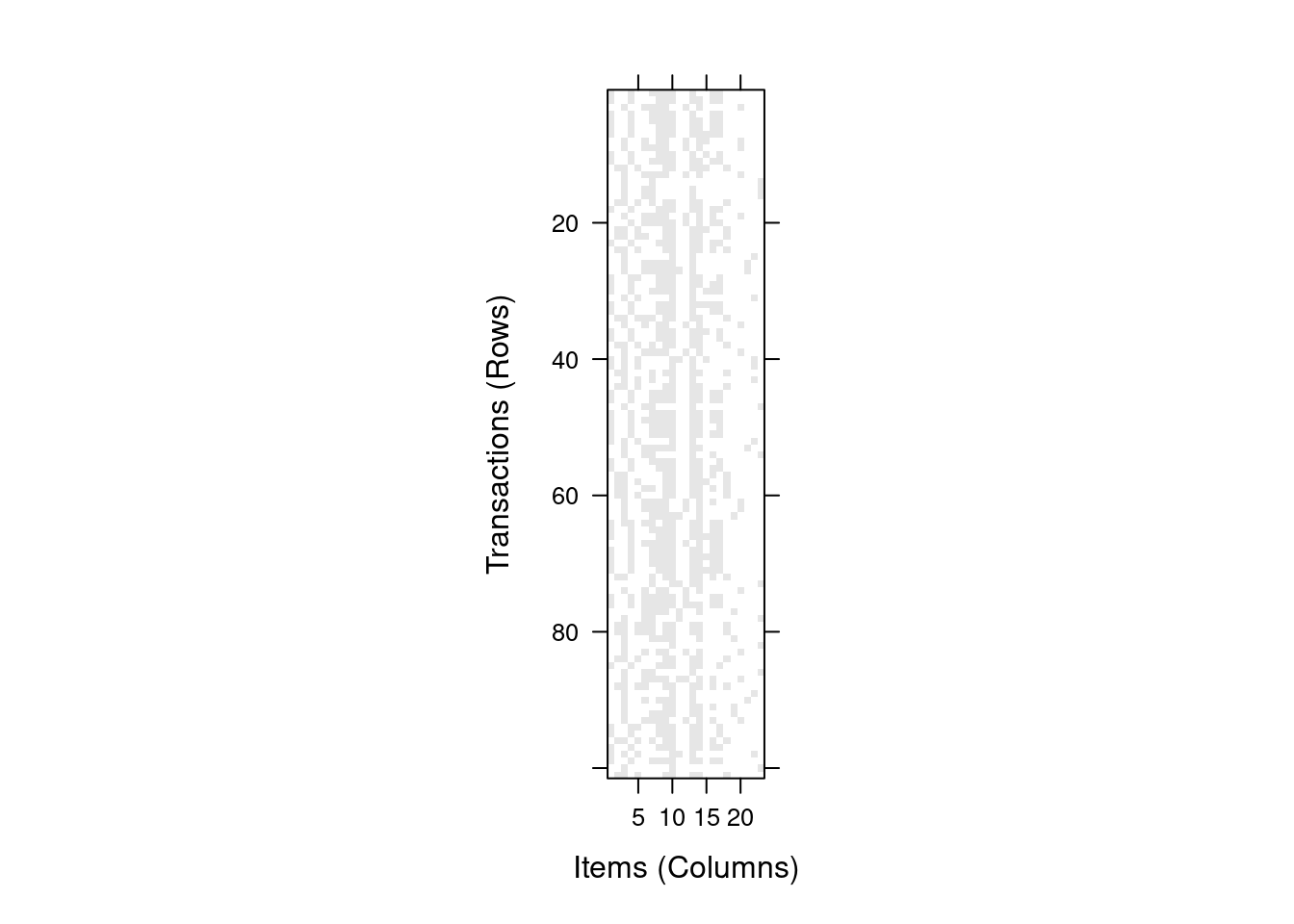
Since each transaction typically only contains a small number of items, it is often more convenient to inspect transactions as sets of items.
inspect(trans[1:3])
## items transactionID
## [1] {hair,
## milk,
## predator,
## toothed,
## backbone,
## breathes,
## legs,
## catsize,
## type=mammal} aardvark
## [2] {hair,
## milk,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## catsize,
## type=mammal} antelope
## [3] {eggs,
## aquatic,
## predator,
## toothed,
## backbone,
## fins,
## tail,
## type=fish} bassIt is often also interesting to look at the relative frequency (=support) of items in the data set. Here we look at the 20 most frequent items.
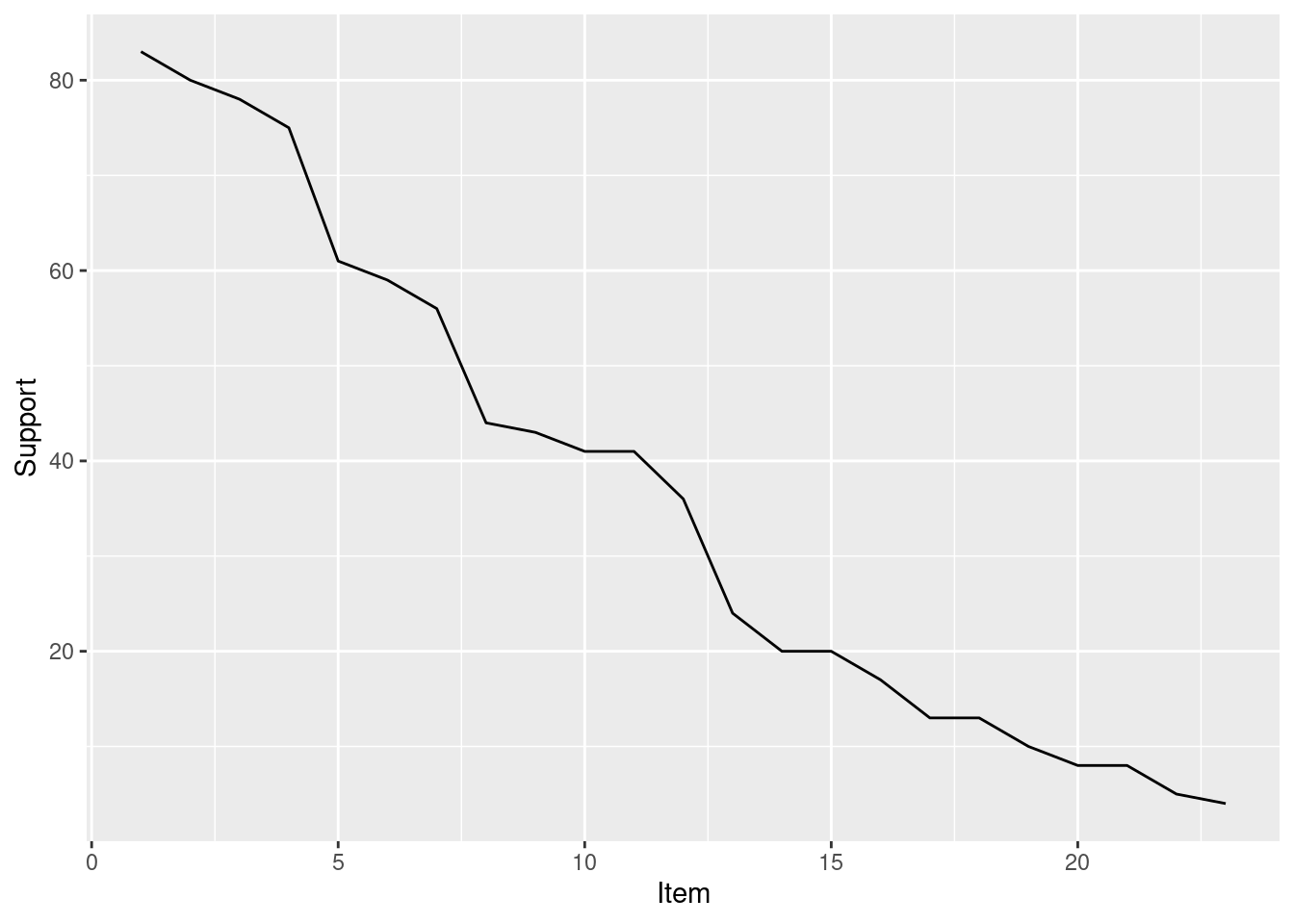
itemFrequencyPlot(trans,topN = 20)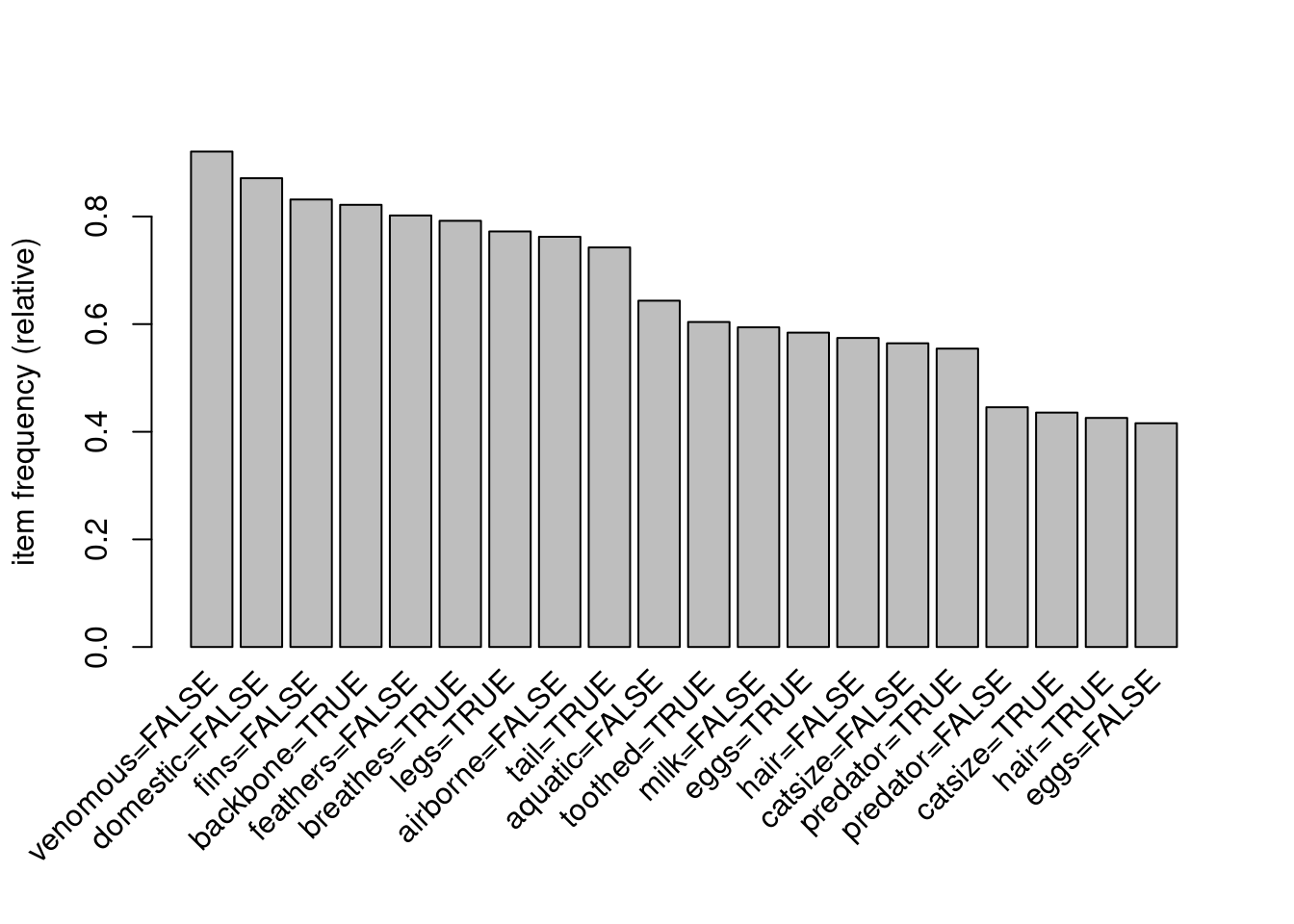
The bar chart only works well for a small number of items. The frequenct distribution over all items can also be shown as a line graph.
ggplot(
tibble(
Support = sort(itemFrequency(trans, type = "absolute"),
decreasing = TRUE),
Item = seq_len(ncol(trans))
), aes(x = Item, y = Support)) +
geom_line()
5.1.2.4 Negative Items
The typical transaction encoding focuses on items for features that the animals have. We can also create items for missing features (e.g., the animal does not lay eggs). This can be easily done by converting the logical values into factors. Now we have a nominal variable with thwo values which will be converted into two items.
sapply(Zoo_has_legs, class)
## hair feathers eggs milk airborne aquatic
## "logical" "logical" "logical" "logical" "logical" "logical"
## predator toothed backbone breathes venomous fins
## "logical" "logical" "logical" "logical" "logical" "logical"
## legs tail domestic catsize type
## "logical" "logical" "logical" "logical" "factor"
Zoo_factors <- Zoo_has_legs |>
mutate(across(where(is.logical), factor))
sapply(Zoo_factors, class)
## hair feathers eggs milk airborne aquatic
## "factor" "factor" "factor" "factor" "factor" "factor"
## predator toothed backbone breathes venomous fins
## "factor" "factor" "factor" "factor" "factor" "factor"
## legs tail domestic catsize type
## "factor" "factor" "factor" "factor" "factor"
summary(Zoo_factors)
## hair feathers eggs milk airborne
## FALSE:58 FALSE:81 FALSE:42 FALSE:60 FALSE:77
## TRUE :43 TRUE :20 TRUE :59 TRUE :41 TRUE :24
##
##
##
##
##
## aquatic predator toothed backbone breathes
## FALSE:65 FALSE:45 FALSE:40 FALSE:18 FALSE:21
## TRUE :36 TRUE :56 TRUE :61 TRUE :83 TRUE :80
##
##
##
##
##
## venomous fins legs tail domestic
## FALSE:93 FALSE:84 FALSE:23 FALSE:26 FALSE:88
## TRUE : 8 TRUE :17 TRUE :78 TRUE :75 TRUE :13
##
##
##
##
##
## catsize type
## FALSE:57 mammal :41
## TRUE :44 bird :20
## reptile : 5
## fish :13
## amphibian : 4
## insect : 8
## mollusc.et.al:10
trans_factors <- transactions(Zoo_factors)
trans_factors
## transactions in sparse format with
## 101 transactions (rows) and
## 39 items (columns)
itemFrequencyPlot(trans_factors, topN = 20)
## Select transactions that contain a certain item
trans_insects <- trans_factors[trans %in% "type=insect"]
trans_insects
## transactions in sparse format with
## 8 transactions (rows) and
## 39 items (columns)
inspect(trans_insects)
## items transactionID
## [1] {hair=FALSE,
## feathers=FALSE,
## eggs=TRUE,
## milk=FALSE,
## airborne=FALSE,
## aquatic=FALSE,
## predator=FALSE,
## toothed=FALSE,
## backbone=FALSE,
## breathes=TRUE,
## venomous=FALSE,
## fins=FALSE,
## legs=TRUE,
## tail=FALSE,
## domestic=FALSE,
## catsize=FALSE,
## type=insect} flea
## [2] {hair=FALSE,
## feathers=FALSE,
## eggs=TRUE,
## milk=FALSE,
## airborne=TRUE,
## aquatic=FALSE,
## predator=FALSE,
## toothed=FALSE,
## backbone=FALSE,
## breathes=TRUE,
## venomous=FALSE,
## fins=FALSE,
## legs=TRUE,
## tail=FALSE,
## domestic=FALSE,
## catsize=FALSE,
## type=insect} gnat
## [3] {hair=TRUE,
## feathers=FALSE,
## eggs=TRUE,
## milk=FALSE,
## airborne=TRUE,
## aquatic=FALSE,
## predator=FALSE,
## toothed=FALSE,
## backbone=FALSE,
## breathes=TRUE,
## venomous=TRUE,
## fins=FALSE,
## legs=TRUE,
## tail=FALSE,
## domestic=TRUE,
## catsize=FALSE,
## type=insect} honeybee
## [4] {hair=TRUE,
## feathers=FALSE,
## eggs=TRUE,
## milk=FALSE,
## airborne=TRUE,
## aquatic=FALSE,
## predator=FALSE,
## toothed=FALSE,
## backbone=FALSE,
## breathes=TRUE,
## venomous=FALSE,
## fins=FALSE,
## legs=TRUE,
## tail=FALSE,
## domestic=FALSE,
## catsize=FALSE,
## type=insect} housefly
## [5] {hair=FALSE,
## feathers=FALSE,
## eggs=TRUE,
## milk=FALSE,
## airborne=TRUE,
## aquatic=FALSE,
## predator=TRUE,
## toothed=FALSE,
## backbone=FALSE,
## breathes=TRUE,
## venomous=FALSE,
## fins=FALSE,
## legs=TRUE,
## tail=FALSE,
## domestic=FALSE,
## catsize=FALSE,
## type=insect} ladybird
## [6] {hair=TRUE,
## feathers=FALSE,
## eggs=TRUE,
## milk=FALSE,
## airborne=TRUE,
## aquatic=FALSE,
## predator=FALSE,
## toothed=FALSE,
## backbone=FALSE,
## breathes=TRUE,
## venomous=FALSE,
## fins=FALSE,
## legs=TRUE,
## tail=FALSE,
## domestic=FALSE,
## catsize=FALSE,
## type=insect} moth
## [7] {hair=FALSE,
## feathers=FALSE,
## eggs=TRUE,
## milk=FALSE,
## airborne=FALSE,
## aquatic=FALSE,
## predator=FALSE,
## toothed=FALSE,
## backbone=FALSE,
## breathes=TRUE,
## venomous=FALSE,
## fins=FALSE,
## legs=TRUE,
## tail=FALSE,
## domestic=FALSE,
## catsize=FALSE,
## type=insect} termite
## [8] {hair=TRUE,
## feathers=FALSE,
## eggs=TRUE,
## milk=FALSE,
## airborne=TRUE,
## aquatic=FALSE,
## predator=FALSE,
## toothed=FALSE,
## backbone=FALSE,
## breathes=TRUE,
## venomous=TRUE,
## fins=FALSE,
## legs=TRUE,
## tail=FALSE,
## domestic=FALSE,
## catsize=FALSE,
## type=insect} wasp5.1.2.5 Vertical Layout (Transaction ID Lists)
The default layout for transactions is horizontal layout (i.e. each transaction is a row). The vertical layout represents transaction data as a list of transaction IDs for each item (= transaction ID lists).
vertical <- as(trans, "tidLists")
as(vertical, "matrix")[1:10, 1:5]
## aardvark antelope bass bear boar
## hair TRUE TRUE FALSE TRUE TRUE
## feathers FALSE FALSE FALSE FALSE FALSE
## eggs FALSE FALSE TRUE FALSE FALSE
## milk TRUE TRUE FALSE TRUE TRUE
## airborne FALSE FALSE FALSE FALSE FALSE
## aquatic FALSE FALSE TRUE FALSE FALSE
## predator TRUE FALSE TRUE TRUE TRUE
## toothed TRUE TRUE TRUE TRUE TRUE
## backbone TRUE TRUE TRUE TRUE TRUE
## breathes TRUE TRUE FALSE TRUE TRUE5.2 Frequent Itemset Generation
Even for the small Zoo dataset, we have already a large number of possible itemsets.
2^ncol(trans)
## [1] 8388608Finding frequent itemsets uses the parameter target = "frequent" (the default target
is to directly mine rules).
its <- apriori(trans, parameter=list(target = "frequent"))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime
## NA 0.1 1 none FALSE TRUE 5
## support minlen maxlen target ext
## 0.1 1 10 frequent itemsets TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 10
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[23 item(s), 101 transaction(s)] done [0.00s].
## sorting and recoding items ... [18 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 7 8 9 10
## Warning in apriori(trans, parameter = list(target =
## "frequent")): Mining stopped (maxlen reached). Only
## patterns up to a length of 10 returned!
## done [0.00s].
## sorting transactions ... done [0.00s].
## writing ... [1465 set(s)] done [0.00s].
## creating S4 object ... done [0.00s].
its
## set of 1465 itemsetsThe default minimum support is .1 (10%). Note: The Zoo data set is very small with very few items. For larger datasets, the default minimum support might be too low and you may run out of memory. You probably want to start out with a higher minimum support like .5 (50%) and then work your way down.
We can calculate the support needed to find itemsets that effect at least 5 animals.
5/nrow(trans)
## [1] 0.0495This shows that we need to go down to a minimum support of about 5%.
its <- apriori(trans, parameter=list(target = "frequent",
support = 0.05))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime
## NA 0.1 1 none FALSE TRUE 5
## support minlen maxlen target ext
## 0.05 1 10 frequent itemsets TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 5
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[23 item(s), 101 transaction(s)] done [0.00s].
## sorting and recoding items ... [21 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 7 8 9 10
## Warning in apriori(trans, parameter = list(target =
## "frequent", support = 0.05)): Mining stopped (maxlen
## reached). Only patterns up to a length of 10 returned!
## done [0.00s].
## sorting transactions ... done [0.00s].
## writing ... [2537 set(s)] done [0.00s].
## creating S4 object ... done [0.00s].
its
## set of 2537 itemsetsWe will get many itemsets. We can sort them by support, and show the top 10 itemsets.
its <- sort(its, by = "support")
its |> head(n = 10) |> inspect()
## items support count
## [1] {backbone} 0.8218 83
## [2] {breathes} 0.7921 80
## [3] {legs} 0.7723 78
## [4] {tail} 0.7426 75
## [5] {backbone, tail} 0.7327 74
## [6] {breathes, legs} 0.7228 73
## [7] {backbone, breathes} 0.6832 69
## [8] {backbone, legs} 0.6337 64
## [9] {backbone, breathes, legs} 0.6337 64
## [10] {toothed} 0.6040 61We can also look at the largest frequent itemsets. Large means here many items.
its[size(its) > 8] |> inspect()
## items support count
## [1] {hair,
## milk,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## catsize,
## type=mammal} 0.23762 24
## [2] {hair,
## milk,
## predator,
## toothed,
## backbone,
## breathes,
## legs,
## catsize,
## type=mammal} 0.15842 16
## [3] {hair,
## milk,
## predator,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## type=mammal} 0.14851 15
## [4] {hair,
## milk,
## predator,
## backbone,
## breathes,
## legs,
## tail,
## catsize,
## type=mammal} 0.13861 14
## [5] {hair,
## milk,
## predator,
## toothed,
## breathes,
## legs,
## tail,
## catsize,
## type=mammal} 0.12871 13
## [6] {hair,
## milk,
## predator,
## toothed,
## backbone,
## legs,
## tail,
## catsize,
## type=mammal} 0.12871 13
## [7] {hair,
## milk,
## predator,
## toothed,
## backbone,
## breathes,
## tail,
## catsize,
## type=mammal} 0.12871 13
## [8] {milk,
## predator,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## catsize,
## type=mammal} 0.12871 13
## [9] {hair,
## milk,
## predator,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## catsize} 0.12871 13
## [10] {hair,
## predator,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## catsize,
## type=mammal} 0.12871 13
## [11] {hair,
## milk,
## predator,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## catsize,
## type=mammal} 0.12871 13
## [12] {hair,
## milk,
## toothed,
## backbone,
## breathes,
## legs,
## domestic,
## catsize,
## type=mammal} 0.05941 6
## [13] {hair,
## milk,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## domestic,
## type=mammal} 0.05941 6
## [14] {feathers,
## eggs,
## airborne,
## predator,
## backbone,
## breathes,
## legs,
## tail,
## type=bird} 0.05941 65.3 Rule Generation
We use the APRIORI algorithm (see
? apriori)
rules <- apriori(trans,
parameter = list(support = 0.05,
confidence = 0.9))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime
## 0.9 0.1 1 none FALSE TRUE 5
## support minlen maxlen target ext
## 0.05 1 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 5
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[23 item(s), 101 transaction(s)] done [0.00s].
## sorting and recoding items ... [21 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 7 8 9 10
## Warning in apriori(trans, parameter = list(support = 0.05,
## confidence = 0.9)): Mining stopped (maxlen reached). Only
## patterns up to a length of 10 returned!
## done [0.00s].
## writing ... [7174 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
length(rules)
## [1] 7174
rules |> head() |> inspect()
## lhs rhs support confidence
## [1] {type=insect} => {eggs} 0.07921 1.0
## [2] {type=insect} => {legs} 0.07921 1.0
## [3] {type=insect} => {breathes} 0.07921 1.0
## [4] {type=mollusc.et.al} => {eggs} 0.08911 0.9
## [5] {type=fish} => {fins} 0.12871 1.0
## [6] {type=fish} => {aquatic} 0.12871 1.0
## coverage lift count
## [1] 0.07921 1.712 8
## [2] 0.07921 1.295 8
## [3] 0.07921 1.262 8
## [4] 0.09901 1.541 9
## [5] 0.12871 5.941 13
## [6] 0.12871 2.806 13
rules |> head() |> quality()
## support confidence coverage lift count
## 1 0.07921 1.0 0.07921 1.712 8
## 2 0.07921 1.0 0.07921 1.295 8
## 3 0.07921 1.0 0.07921 1.262 8
## 4 0.08911 0.9 0.09901 1.541 9
## 5 0.12871 1.0 0.12871 5.941 13
## 6 0.12871 1.0 0.12871 2.806 13It is common to sort rules by the lift measure and inspect the rules with the largest lift.
rules <- sort(rules, by = "lift")
rules |> head(n = 10) |> inspect()
## lhs rhs support confidence coverage lift count
## [1] {eggs,
## fins} => {type=fish} 0.12871 1 0.12871 7.769 13
## [2] {eggs,
## aquatic,
## fins} => {type=fish} 0.12871 1 0.12871 7.769 13
## [3] {eggs,
## predator,
## fins} => {type=fish} 0.08911 1 0.08911 7.769 9
## [4] {eggs,
## toothed,
## fins} => {type=fish} 0.12871 1 0.12871 7.769 13
## [5] {eggs,
## fins,
## tail} => {type=fish} 0.12871 1 0.12871 7.769 13
## [6] {eggs,
## backbone,
## fins} => {type=fish} 0.12871 1 0.12871 7.769 13
## [7] {eggs,
## aquatic,
## predator,
## fins} => {type=fish} 0.08911 1 0.08911 7.769 9
## [8] {eggs,
## aquatic,
## toothed,
## fins} => {type=fish} 0.12871 1 0.12871 7.769 13
## [9] {eggs,
## aquatic,
## fins,
## tail} => {type=fish} 0.12871 1 0.12871 7.769 13
## [10] {eggs,
## aquatic,
## backbone,
## fins} => {type=fish} 0.12871 1 0.12871 7.769 13We see that most high-lift rules are about fish. The reason may be since fish have very specific features that are very different from the other animal types in the data.
As a comparison, we show next what rules are generated if we include negative items in the transactions.
r <- apriori(trans_factors)
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime
## 0.8 0.1 1 none FALSE TRUE 5
## support minlen maxlen target ext
## 0.1 1 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 10
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[39 item(s), 101 transaction(s)] done [0.00s].
## sorting and recoding items ... [34 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 7 8 9 10
## Warning in apriori(trans_factors): Mining stopped (maxlen
## reached). Only patterns up to a length of 10 returned!
## done [0.05s].
## writing ... [1517191 rule(s)] done [0.20s].
## creating S4 object ... done [0.62s].
r
## set of 1517191 rulesThis encoding creates very dense data (i.e., each transaction contains many items). This leads to finding many rules and may lead to the algorithm running out of memory. This is how much memory the rule set uses.
print(object.size(r), unit = "Mb")
## 110.2 MbLet’s inspect the top 10 lift rules.
inspect(r[1:10])
## lhs rhs support confidence
## [1] {} => {feathers=FALSE} 0.8020 0.8020
## [2] {} => {backbone=TRUE} 0.8218 0.8218
## [3] {} => {fins=FALSE} 0.8317 0.8317
## [4] {} => {domestic=FALSE} 0.8713 0.8713
## [5] {} => {venomous=FALSE} 0.9208 0.9208
## [6] {domestic=TRUE} => {predator=FALSE} 0.1089 0.8462
## [7] {domestic=TRUE} => {aquatic=FALSE} 0.1188 0.9231
## [8] {domestic=TRUE} => {legs=TRUE} 0.1188 0.9231
## [9] {domestic=TRUE} => {breathes=TRUE} 0.1188 0.9231
## [10] {domestic=TRUE} => {backbone=TRUE} 0.1188 0.9231
## coverage lift count
## [1] 1.0000 1.000 81
## [2] 1.0000 1.000 83
## [3] 1.0000 1.000 84
## [4] 1.0000 1.000 88
## [5] 1.0000 1.000 93
## [6] 0.1287 1.899 11
## [7] 0.1287 1.434 12
## [8] 0.1287 1.195 12
## [9] 0.1287 1.165 12
## [10] 0.1287 1.123 12
r |> head(n = 10, by = "lift") |> inspect()
## lhs rhs support confidence coverage lift count
## [1] {breathes=FALSE,
## fins=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [2] {eggs=TRUE,
## fins=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [3] {milk=FALSE,
## fins=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [4] {breathes=FALSE,
## fins=TRUE,
## legs=FALSE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [5] {aquatic=TRUE,
## breathes=FALSE,
## fins=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [6] {hair=FALSE,
## breathes=FALSE,
## fins=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [7] {eggs=TRUE,
## breathes=FALSE,
## fins=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [8] {milk=FALSE,
## breathes=FALSE,
## fins=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [9] {toothed=TRUE,
## breathes=FALSE,
## fins=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13
## [10] {breathes=FALSE,
## fins=TRUE,
## tail=TRUE} => {type=fish} 0.1287 1 0.1287 7.769 13The rules are similar, but now show that fish do not breathe (air) or give milk. It is often benficial to introduce negative items for some features, but not for all.
5.3.1 Additional Interest Measures
Many different interest measures can be calculated for existing rules
(or itemsets) using the function
interestMeasure().
interestMeasure(rules[1:10], measure = c("phi", "gini"),
trans = trans)
## phi gini
## 1 1.0000 0.2243
## 2 1.0000 0.2243
## 3 0.8138 0.1485
## 4 1.0000 0.2243
## 5 1.0000 0.2243
## 6 1.0000 0.2243
## 7 0.8138 0.1485
## 8 1.0000 0.2243
## 9 1.0000 0.2243
## 10 1.0000 0.2243To store the new interest measures with the rule set, we have to add them to the quality slot.
quality(rules) <- cbind(quality(rules),
interestMeasure(rules, measure = c("phi", "gini"),
trans = trans))Find rules which score high for Phi correlation between the LHS and RHS of the rule.
rules |> head(by = "phi") |> inspect()
## lhs rhs support confidence coverage lift count phi gini
## [1] {eggs,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13 1 0.2243
## [2] {eggs,
## aquatic,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13 1 0.2243
## [3] {eggs,
## toothed,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13 1 0.2243
## [4] {eggs,
## fins,
## tail} => {type=fish} 0.1287 1 0.1287 7.769 13 1 0.2243
## [5] {eggs,
## backbone,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13 1 0.2243
## [6] {eggs,
## aquatic,
## toothed,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13 1 0.22435.3.2 Mine Using Templates
Sometimes it is beneficial to specify what items should be where in the found
rule. Forapriori() we can use the parameter appearance to specify this
(see
? APappearance).
In the following we restrict rules to an animal type in the RHS and
any item in the LHS. We first create all type related items.
type <- grep("type=", itemLabels(trans), value = TRUE)
type
## [1] "type=mammal" "type=bird"
## [3] "type=reptile" "type=fish"
## [5] "type=amphibian" "type=insect"
## [7] "type=mollusc.et.al"Now, we can restrict the appearance in the RHS.
rules_type <- apriori(trans, appearance= list(rhs = type))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime
## 0.8 0.1 1 none FALSE TRUE 5
## support minlen maxlen target ext
## 0.1 1 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 10
##
## set item appearances ...[7 item(s)] done [0.00s].
## set transactions ...[23 item(s), 101 transaction(s)] done [0.00s].
## sorting and recoding items ... [18 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 7 8 9 10
## Warning in apriori(trans, appearance = list(rhs = type)):
## Mining stopped (maxlen reached). Only patterns up to a
## length of 10 returned!
## done [0.00s].
## writing ... [571 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
rules_type |> sort(by = "lift") |> head() |> inspect()
## lhs rhs support confidence coverage lift count
## [1] {eggs,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13
## [2] {eggs,
## aquatic,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13
## [3] {eggs,
## toothed,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13
## [4] {eggs,
## fins,
## tail} => {type=fish} 0.1287 1 0.1287 7.769 13
## [5] {eggs,
## backbone,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 13
## [6] {eggs,
## aquatic,
## toothed,
## fins} => {type=fish} 0.1287 1 0.1287 7.769 135.3.3 Redundant Rules
Association rule mining is prone to generate too many very specific rules. A rule can be defined as redundant if a more general rules with the same or a higher confidence exists.
rules_type
## set of 571 rules
table(size(rules_type))
##
## 2 3 4 5 6 7 8 9 10
## 3 29 95 155 150 92 37 9 1
rules_type_non_redundant <- rules_type[!is.redundant(rules_type)]
rules_type_non_redundant
## set of 29 rules
table(size(rules_type_non_redundant))
##
## 2 3 4 5
## 3 13 10 3
inspect(rules_type_non_redundant)
## lhs rhs support confidence coverage lift count
## [1] {feathers} => {type=bird} 0.1980 1.0000 0.1980 5.050 20
## [2] {milk} => {type=mammal} 0.4059 1.0000 0.4059 2.463 41
## [3] {hair} => {type=mammal} 0.3861 0.9070 0.4257 2.234 39
## [4] {eggs,
## fins} => {type=fish} 0.1287 1.0000 0.1287 7.769 13
## [5] {fins,
## tail} => {type=fish} 0.1287 0.8125 0.1584 6.312 13
## [6] {airborne,
## tail} => {type=bird} 0.1584 0.8889 0.1782 4.489 16
## [7] {airborne,
## backbone} => {type=bird} 0.1584 0.8889 0.1782 4.489 16
## [8] {hair,
## catsize} => {type=mammal} 0.2970 1.0000 0.2970 2.463 30
## [9] {hair,
## predator} => {type=mammal} 0.1980 1.0000 0.1980 2.463 20
## [10] {hair,
## toothed} => {type=mammal} 0.3762 1.0000 0.3762 2.463 38
## [11] {hair,
## tail} => {type=mammal} 0.3267 1.0000 0.3267 2.463 33
## [12] {hair,
## backbone} => {type=mammal} 0.3861 1.0000 0.3861 2.463 39
## [13] {toothed,
## catsize} => {type=mammal} 0.3069 0.8857 0.3465 2.182 31
## [14] {breathes,
## catsize} => {type=mammal} 0.3168 0.8205 0.3861 2.021 32
## [15] {toothed,
## legs} => {type=mammal} 0.3663 0.8810 0.4158 2.170 37
## [16] {toothed,
## breathes} => {type=mammal} 0.3960 0.8511 0.4653 2.097 40
## [17] {eggs,
## airborne,
## tail} => {type=bird} 0.1584 1.0000 0.1584 5.050 16
## [18] {eggs,
## airborne,
## backbone} => {type=bird} 0.1584 1.0000 0.1584 5.050 16
## [19] {eggs,
## legs,
## tail} => {type=bird} 0.1980 0.8333 0.2376 4.208 20
## [20] {predator,
## legs,
## catsize} => {type=mammal} 0.1683 0.8095 0.2079 1.994 17
## [21] {predator,
## breathes,
## catsize} => {type=mammal} 0.1980 0.8696 0.2277 2.142 20
## [22] {toothed,
## legs,
## catsize} => {type=mammal} 0.2772 1.0000 0.2772 2.463 28
## [23] {toothed,
## breathes,
## catsize} => {type=mammal} 0.3069 1.0000 0.3069 2.463 31
## [24] {backbone,
## legs,
## catsize} => {type=mammal} 0.2871 0.8056 0.3564 1.984 29
## [25] {toothed,
## legs,
## tail} => {type=mammal} 0.3168 0.9412 0.3366 2.319 32
## [26] {toothed,
## breathes,
## tail} => {type=mammal} 0.3366 0.8947 0.3762 2.204 34
## [27] {eggs,
## aquatic,
## toothed,
## tail} => {type=fish} 0.1287 0.9286 0.1386 7.214 13
## [28] {predator,
## legs,
## tail,
## catsize} => {type=mammal} 0.1386 0.8235 0.1683 2.029 14
## [29] {predator,
## backbone,
## legs,
## catsize} => {type=mammal} 0.1683 0.8500 0.1980 2.094 17We see that this simple redundancy check results in a rule set of a manageable size which can can be easily analyzed by a human.
5.4 Compact Representation of Frequent Itemsets
An itemset is maximal in a set if no proper superset of the itemset is contained in the set. Since we are often interest in the most specific itemsets with the largest number of items this is often useful for reducing the size of the set for manual inspection.
its_max <- its[is.maximal(its)]
its_max
## set of 22 itemsets
its_max |> head(by = "support") |> inspect()
## items support count
## [1] {hair,
## milk,
## predator,
## toothed,
## backbone,
## breathes,
## legs,
## tail,
## catsize,
## type=mammal} 0.12871 13
## [2] {eggs,
## aquatic,
## predator,
## toothed,
## backbone,
## fins,
## tail,
## type=fish} 0.08911 9
## [3] {aquatic,
## predator,
## toothed,
## backbone,
## breathes} 0.07921 8
## [4] {aquatic,
## predator,
## toothed,
## backbone,
## fins,
## tail,
## catsize} 0.06931 7
## [5] {eggs,
## venomous} 0.05941 6
## [6] {predator,
## venomous} 0.05941 6Another compact representation is the idea of closed itemsets. The closure of an itemset is its largest proper superset which has the same support (is contained in exactly the same transactions). An itemset is closed, if it is its own closure. This is similar to the idea of maximal itemsets but only removes itemsets if a superset with the same support exists.
its_closed <- its[is.closed(its)]
its_closed
## set of 230 itemsets
its_closed |> head(by = "support") |> inspect()
## items support count
## [1] {backbone} 0.8218 83
## [2] {breathes} 0.7921 80
## [3] {legs} 0.7723 78
## [4] {tail} 0.7426 75
## [5] {backbone, tail} 0.7327 74
## [6] {breathes, legs} 0.7228 73Here is a comparison of the number of frequent itemsets with closed and maximal itemsets.
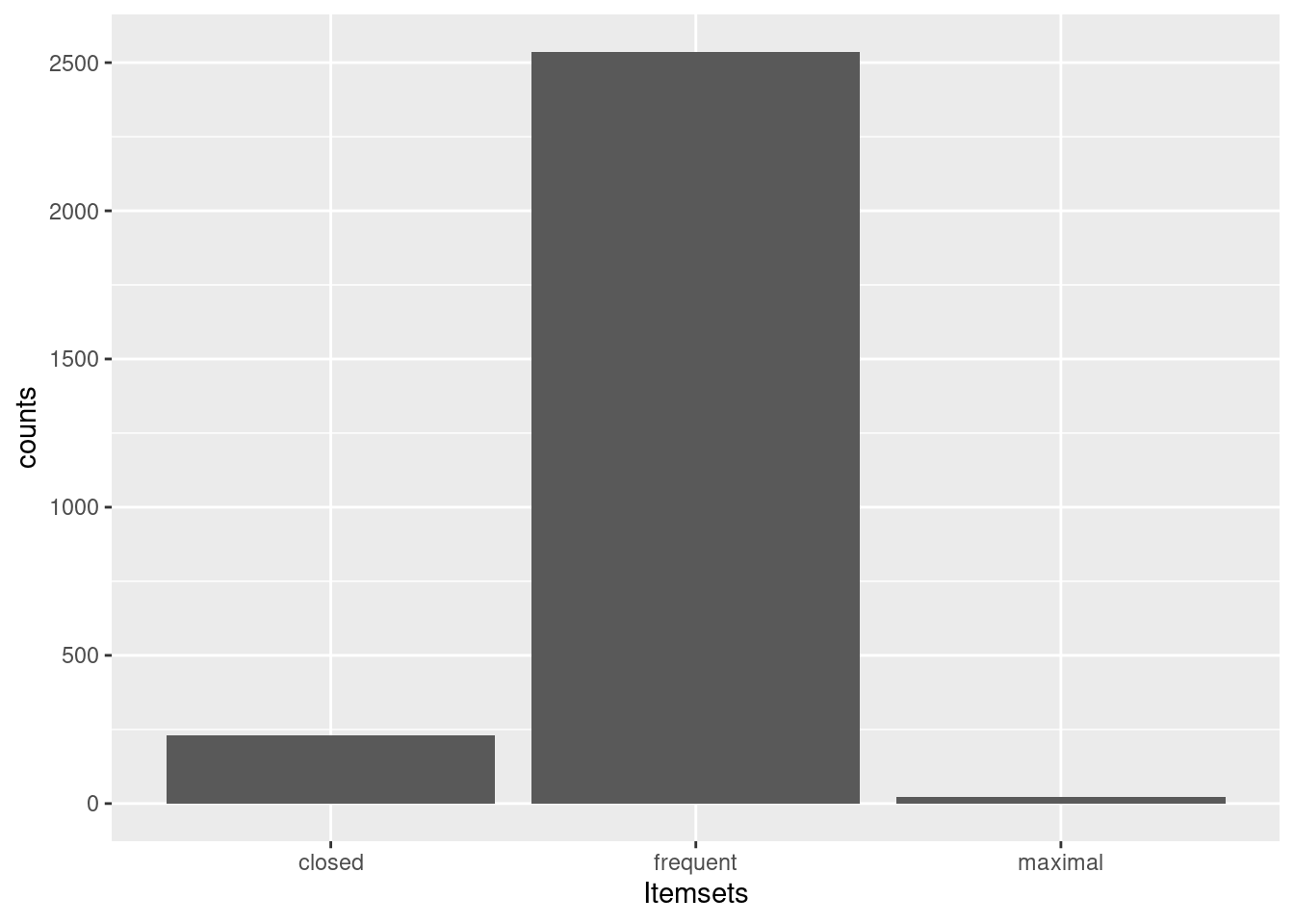
ggplot(as_tibble(counts, rownames = "Itemsets"),
aes(Itemsets, counts)) + geom_bar(stat = "identity")
5.5 Association Rule Visualization*
Visualization is a very powerful approach to analyse large sets of mined association rules and frequent itemsets. We present here some options to create static visualizations and inspect rule sets interactively.
5.5.1 Static Visualizations
Load the arulesViz library.
Create rules for the Zoo dataset converting the legs variable into a binary indicator.
data(Zoo, package = "mlbench")
Zoo_has_legs <- Zoo |> mutate(legs = legs > 0)
trans <- transactions(Zoo_has_legs)
trans
## transactions in sparse format with
## 101 transactions (rows) and
## 23 items (columns)
rules <- apriori(trans,
parameter = list(support = 0.05,
confidence = 0.9))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime
## 0.9 0.1 1 none FALSE TRUE 5
## support minlen maxlen target ext
## 0.05 1 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 5
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[23 item(s), 101 transaction(s)] done [0.00s].
## sorting and recoding items ... [21 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 6 7 8 9 10
## Warning in apriori(trans, parameter = list(support = 0.05,
## confidence = 0.9)): Mining stopped (maxlen reached). Only
## patterns up to a length of 10 returned!
## done [0.00s].
## writing ... [7174 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
quality(rules) <- cbind(quality(rules),
interestMeasure(rules, measure = c("phi", "gini"),
trans = trans))
rules
## set of 7174 rules5.5.1.1 Scatterplot
The default plot for association rules is a support/confidence scatterplot.
plot(rules)
## To reduce overplotting, jitter is added! Use jitter = 0 to prevent jitter.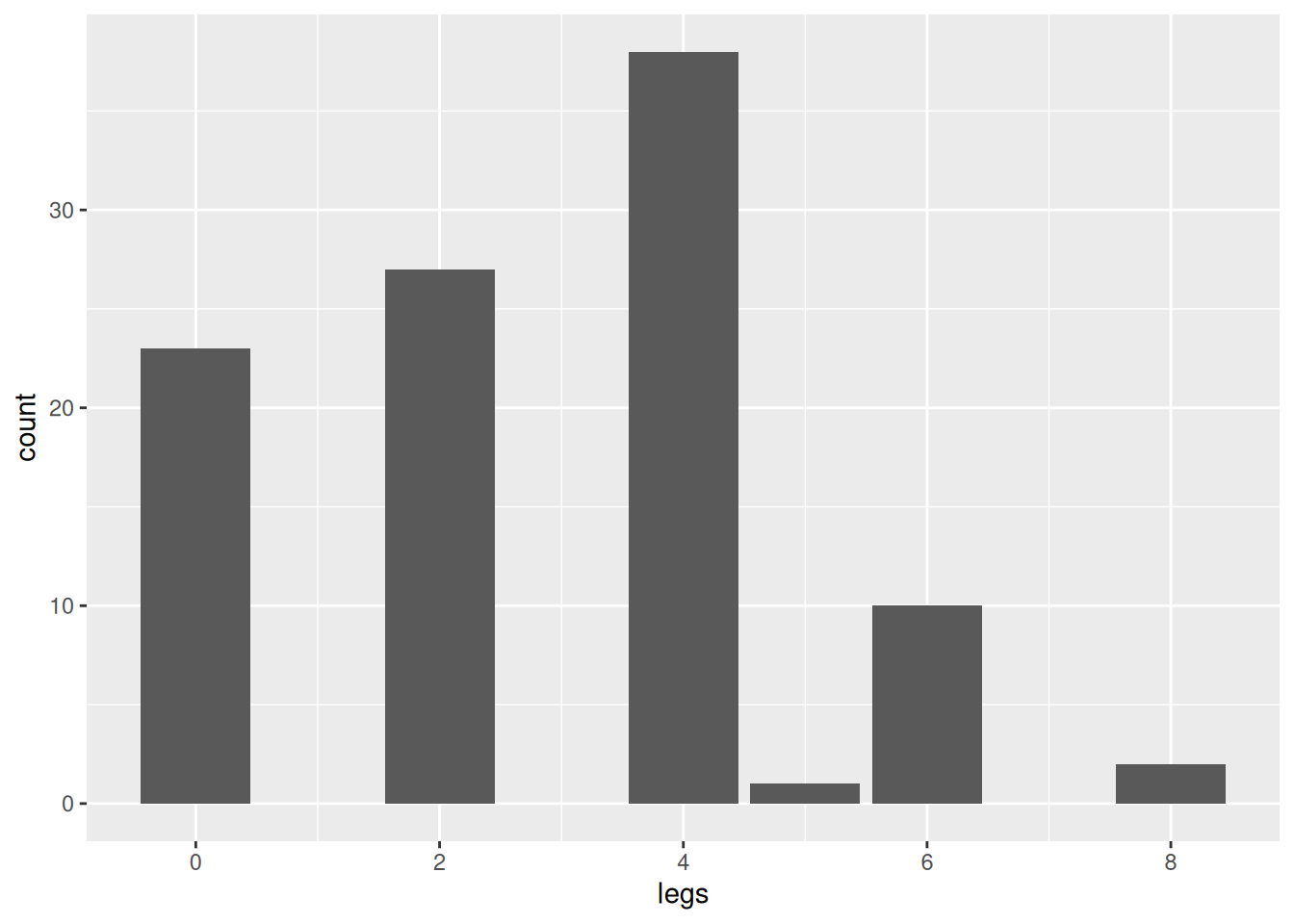
Each rules is represented by a point. Note that some jitter (randomly move points) was added to show how many rules have the same confidence and support value. Without jitter:
plot(rules, shading = "order")
## To reduce overplotting, jitter is added! Use jitter = 0 to prevent jitter.
5.5.1.2 Grouped Matrix Plot
The grouped matrix plot tries to group rules with a similar relationship between the rule’s LHS and RHS and represents the groups support and lift using a balloon plot. Grouping is performed using clustering. Groups are organized such that the most interesting rules appear to the top left corner.
set.seed(1234)
plot(rules, method = "grouped matrix")
## Registered S3 methods overwritten by 'registry':
## method from
## print.registry_field proxy
## print.registry_entry proxy
The most interesting rules are about thre relationship between fins, eggs and 5 more items and the type fish.
This plot can also be used interactively using the parameter
engine = "interactive".
5.5.1.3 Gaph-based Visualization
Graph-based techniques visualize association rules using vertices and edges, where vertices typically represent items or itemsets and edges indicate relationships in terms of rules. Interest measures are typically added to the plot as labels on the edges or by color or width of the arrows displaying the edges.
plot(rules, method = "graph")
## Warning: Too many rules supplied. Only plotting the best
## 100 using 'lift' (change control parameter max if needed).
 We see that the automatic graph layout organizes the rules roughly into three groups
representing the three most frequent animal types: birds, mammals and fish.
we can also see that birds and mammals share items like breathes while birds and
fish share eggs.
We see that the automatic graph layout organizes the rules roughly into three groups
representing the three most frequent animal types: birds, mammals and fish.
we can also see that birds and mammals share items like breathes while birds and
fish share eggs.5.5.2 Interactive Visualizations
Interactive visualizations let the user explore the large number of rules and itemsets and learn about the structure of the data. The overview article arulesViz: Interactive Visualization of Association Rules with R provides an in-depth discussion of interactive association rule visualization.
We will use the association rules mined from the Iris dataset for the following examples.
data(iris)
summary(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.30 Min. :2.00 Min. :1.00 Min. :0.1
## 1st Qu.:5.10 1st Qu.:2.80 1st Qu.:1.60 1st Qu.:0.3
## Median :5.80 Median :3.00 Median :4.35 Median :1.3
## Mean :5.84 Mean :3.06 Mean :3.76 Mean :1.2
## 3rd Qu.:6.40 3rd Qu.:3.30 3rd Qu.:5.10 3rd Qu.:1.8
## Max. :7.90 Max. :4.40 Max. :6.90 Max. :2.5
## Species
## setosa :50
## versicolor:50
## virginica :50
##
##
## Convert the data to transactions.
iris_trans <- transactions(iris)
## Warning: Column(s) 1, 2, 3, 4 not logical or factor.
## Applying default discretization (see '? discretizeDF').Note that this conversion gives a warning to indicate that some potentially unwanted conversion happens. Some features are numeric and need to be discretized. The conversion automatically applies frequency-based discretization with 3 classes to each numeric feature, however, the use may want to use a different discretization strategy.
iris_trans |> head() |> inspect()
## items transactionID
## [1] {Sepal.Length=[4.3,5.4),
## Sepal.Width=[3.2,4.4],
## Petal.Length=[1,2.63),
## Petal.Width=[0.1,0.867),
## Species=setosa} 1
## [2] {Sepal.Length=[4.3,5.4),
## Sepal.Width=[2.9,3.2),
## Petal.Length=[1,2.63),
## Petal.Width=[0.1,0.867),
## Species=setosa} 2
## [3] {Sepal.Length=[4.3,5.4),
## Sepal.Width=[3.2,4.4],
## Petal.Length=[1,2.63),
## Petal.Width=[0.1,0.867),
## Species=setosa} 3
## [4] {Sepal.Length=[4.3,5.4),
## Sepal.Width=[2.9,3.2),
## Petal.Length=[1,2.63),
## Petal.Width=[0.1,0.867),
## Species=setosa} 4
## [5] {Sepal.Length=[4.3,5.4),
## Sepal.Width=[3.2,4.4],
## Petal.Length=[1,2.63),
## Petal.Width=[0.1,0.867),
## Species=setosa} 5
## [6] {Sepal.Length=[5.4,6.3),
## Sepal.Width=[3.2,4.4],
## Petal.Length=[1,2.63),
## Petal.Width=[0.1,0.867),
## Species=setosa} 6Next, we mine association rules.
rules <- apriori(iris_trans, parameter = list(support = 0.1,
confidence = 0.8))
## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime
## 0.8 0.1 1 none FALSE TRUE 5
## support minlen maxlen target ext
## 0.1 1 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 15
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[15 item(s), 150 transaction(s)] done [0.00s].
## sorting and recoding items ... [15 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 5 done [0.00s].
## writing ... [144 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].
rules
## set of 144 rules5.5.2.1 Interactive Inspect With Sorting, Filtering and Paging
An interactive table that lets the user sort and filter the rules is a very effective exploration tool. We can quickly find the highest lift rules and filter by interesting items in the LHS and RHS of the rules.
5.5.2.2 Scatter Plot
Plot rules as a scatter plot using an interactive html widget. To avoid
overplotting, jitter is added automatically. Set jitter = 0 to disable
jitter. Hovering over rules shows rule information. Note:
plotly/javascript does not do well with too many points, so plot selects
the top 1000 rules with a warning if more rules are supplied.
plot(rules, engine = "html")
## To reduce overplotting, jitter is added! Use jitter = 0 to prevent jitter.5.5.2.3 Matrix Visualization
The rules are organized in a matrix where the columns represent unique LHS itemsets and the rows are the RHS items. Hovering over rules shows rule information.
plot(rules, method = "matrix", engine = "html") 5.5.2.4 Visualization as Graph
Plot rules as an interactive graph with items as rectangular vertices and rules as circular vertices. Hovering over a vertex shows additional information. On most devices, the mouse wheel lets the user zoom in and out of the graph. Note: the used javascript library does not do well with too many graph nodes, so plot selects the top 100 rules only (with a warning).
plot(rules, method = "graph", engine = "html")
## Warning: Too many rules supplied. Only plotting the best
## 100 using 'lift' (change control parameter max if needed).5.5.2.5 Interactive Rule Explorer
You can specify a rule set or a dataset. To explore rules that can be
mined from iris, use: ruleExplorer(iris)
The rule explorer creates an interactive Shiny application that can be used locally or deployed on a server for sharing. A deployed version of the ruleExplorer is available here (using shinyapps.io).
5.6 Exercises*
We will again use the Palmer penguin data for the exercises.
library(palmerpenguins)
head(penguins)
## # A tibble: 6 × 8
## species island bill_length_mm bill_depth_mm
## <chr> <chr> <dbl> <dbl>
## 1 Adelie Torgersen 39.1 18.7
## 2 Adelie Torgersen 39.5 17.4
## 3 Adelie Torgersen 40.3 18
## 4 Adelie Torgersen NA NA
## 5 Adelie Torgersen 36.7 19.3
## 6 Adelie Torgersen 39.3 20.6
## # ℹ 4 more variables: flipper_length_mm <dbl>,
## # body_mass_g <dbl>, sex <chr>, year <dbl>- Translate the penguin data into transaction data with:
trans <- transactions(penguins)
## Warning: Column(s) 1, 2, 3, 4, 5, 6, 7, 8 not logical or
## factor. Applying default discretization (see '?
## discretizeDF').
## Warning in discretize(x = c(2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, : The calculated breaks are: 2007, 2008, 2009, 2009
## Only unique breaks are used reducing the number of intervals. Look at ? discretize for details.
trans
## transactions in sparse format with
## 344 transactions (rows) and
## 22 items (columns)Why does the conversion report warnings?
- What do the following first three transactions mean?
inspect(trans[1:3])
## items transactionID
## [1] {species=Adelie,
## island=Torgersen,
## bill_length_mm=[32.1,40.8),
## bill_depth_mm=[18.3,21.5],
## flipper_length_mm=[172,192),
## body_mass_g=[3.7e+03,4.55e+03),
## sex=male,
## year=[2007,2008)} 1
## [2] {species=Adelie,
## island=Torgersen,
## bill_length_mm=[32.1,40.8),
## bill_depth_mm=[16.2,18.3),
## flipper_length_mm=[172,192),
## body_mass_g=[3.7e+03,4.55e+03),
## sex=female,
## year=[2007,2008)} 2
## [3] {species=Adelie,
## island=Torgersen,
## bill_length_mm=[32.1,40.8),
## bill_depth_mm=[16.2,18.3),
## flipper_length_mm=[192,209),
## body_mass_g=[2.7e+03,3.7e+03),
## sex=female,
## year=[2007,2008)} 3Next, use the ruleExplorer() function to analyze association rules
created for the transaction data set.
Use the default settings for the parameters. Using the Data Table, what is the association rule with the highest lift. What does its LHS, RHS, support, confidence and lift mean?
Use the Graph visualization. Use select by id to highlight different species and different islands and then hover over some of the rules. What do you see?