3 Classification: Basic Concepts

This chapter introduces decision trees for classification and discusses how models are built and evaluated.

The corresponding chapter of the data mining textbook is available online: Chapter 3: Classification: Basic Concepts and Techniques.

Packages Used in this Chapter

pkgs <- c("basemodels", "caret", "FSelector", "lattice", "mlbench", 
          "palmerpenguins", "party", "pROC", "rpart", 
          "rpart.plot", "tidyverse")

pkgs_install <- pkgs[!(pkgs %in% installed.packages()[,"Package"])]
if(length(pkgs_install)) install.packages(pkgs_install)

The packages used for this chapter are:

basemodels (Y.-J. Chen et al. 2023)
caret (Kuhn 2023)
FSelector (Romanski, Kotthoff, and Schratz 2023)
lattice (Sarkar 2023)
mlbench (Leisch and Dimitriadou 2024)
palmerpenguins (Horst, Hill, and Gorman 2022)
party (Hothorn et al. 2024)
pROC (Robin et al. 2023)
rpart (Therneau and Atkinson 2023)
rpart.plot (Milborrow 2024)
tidyverse (Wickham 2023c)

In the examples in this book, we use the popular machine learning R package caret. It makes preparing training sets, building classification (and regression) models and evaluation easier. A great cheat sheet can be found here.

A newer R framework for machine learning is tidymodels, a set of packages that integrate more naturally with tidyverse. Using tidymodels, or any other framework (e.g., Python’s scikit-learn) should be relatively easy after learning the concepts using caret.

3.1 Basic Concepts

Classification is a machine learning task with the goal to learn a predictive function of the form

\[y = f(\mathbf{x}),\]

where $\mathbf{x}$ is called the attribute set and $y$ the class label. The attribute set consists of feature which describe an object. These features can be measured using any scale (i.e., nominal, interval, …). The class label is a nominal attribute. It it is a binary attribute, then the problem is called a binary classification problem.

Classification learns the classification model from training data where both the features and the correct class label are available. This is why it is called a supervised learning problem.

A related supervised learning problem is regression, where $y$ is a number instead of a label. Linear regression is a very popular supervised learning model which is taught in almost any introductory statistics course. Code examples for regression are available in the extra Chapter Regression*.

This chapter will introduce decision trees, model evaluation and comparison, feature selection, and then explore methods to handle the class imbalance problem.

You can read the free sample chapter from the textbook (Tan, Steinbach, and Kumar 2005): Chapter 3. Classification: Basic Concepts and Techniques

3.2 General Framework for Classification

Supervised learning has two steps:

Induction: Training a model on training data with known class labels.
Deduction: Predicting class labels for new data.

We often test model by predicting the class for data where we know the correct label. We test the model on test data with known labels and can then calculate the error by comparing the prediction with the known correct label. It is tempting to measure how well the model has learned the training data, by testing it on the training data. The error on the training data is called resubstitution error. It does not help us to find out if the model generalizes well to new data that was not part of the training.

We typically want to evaluate how well the model generalizes new data, so it is important that the test data and the training data do not overlap. We call the error on proper test data the generalization error.

This chapter builds up the needed concepts. A complete example of how to perform model selection and estimate the generalization error is in the section Hyperparameter Tuning.

3.2.1 The Zoo Dataset

To demonstrate classification, we will use the Zoo dataset which is included in the R package mlbench (you may have to install it). The Zoo dataset containing 17 (mostly logical) variables for 101 animals as a data frame with 17 columns (hair, feathers, eggs, milk, airborne, aquatic, predator, toothed, backbone, breathes, venomous, fins, legs, tail, domestic, catsize, type). The first 16 columns represent the feature vector $\mathbf{x}$ and the last column called type is the class label $y$. We convert the data frame into a tidyverse tibble (optional).

data(Zoo, package="mlbench")
head(Zoo)
##           hair feathers  eggs  milk airborne aquatic
## aardvark  TRUE    FALSE FALSE  TRUE    FALSE   FALSE
## antelope  TRUE    FALSE FALSE  TRUE    FALSE   FALSE
## bass     FALSE    FALSE  TRUE FALSE    FALSE    TRUE
## bear      TRUE    FALSE FALSE  TRUE    FALSE   FALSE
## boar      TRUE    FALSE FALSE  TRUE    FALSE   FALSE
## buffalo   TRUE    FALSE FALSE  TRUE    FALSE   FALSE
##          predator toothed backbone breathes venomous  fins
## aardvark     TRUE    TRUE     TRUE     TRUE    FALSE FALSE
## antelope    FALSE    TRUE     TRUE     TRUE    FALSE FALSE
## bass         TRUE    TRUE     TRUE    FALSE    FALSE  TRUE
## bear         TRUE    TRUE     TRUE     TRUE    FALSE FALSE
## boar         TRUE    TRUE     TRUE     TRUE    FALSE FALSE
## buffalo     FALSE    TRUE     TRUE     TRUE    FALSE FALSE
##          legs  tail domestic catsize   type
## aardvark    4 FALSE    FALSE    TRUE mammal
## antelope    4  TRUE    FALSE    TRUE mammal
## bass        0  TRUE    FALSE   FALSE   fish
## bear        4 FALSE    FALSE    TRUE mammal
## boar        4  TRUE    FALSE    TRUE mammal
## buffalo     4  TRUE    FALSE    TRUE mammal

Note: data.frames in R can have row names. The Zoo data set uses the animal name as the row names. tibbles from tidyverse do not support row names. To keep the animal name you can add a column with the animal name.

library(tidyverse)
as_tibble(Zoo, rownames = "animal")
## # A tibble: 101 × 18
##    animal   hair  feathers eggs  milk  airborne aquatic
##    <chr>    <lgl> <lgl>    <lgl> <lgl> <lgl>    <lgl>  
##  1 aardvark TRUE  FALSE    FALSE TRUE  FALSE    FALSE  
##  2 antelope TRUE  FALSE    FALSE TRUE  FALSE    FALSE  
##  3 bass     FALSE FALSE    TRUE  FALSE FALSE    TRUE   
##  4 bear     TRUE  FALSE    FALSE TRUE  FALSE    FALSE  
##  5 boar     TRUE  FALSE    FALSE TRUE  FALSE    FALSE  
##  6 buffalo  TRUE  FALSE    FALSE TRUE  FALSE    FALSE  
##  7 calf     TRUE  FALSE    FALSE TRUE  FALSE    FALSE  
##  8 carp     FALSE FALSE    TRUE  FALSE FALSE    TRUE   
##  9 catfish  FALSE FALSE    TRUE  FALSE FALSE    TRUE   
## 10 cavy     TRUE  FALSE    FALSE TRUE  FALSE    FALSE  
## # ℹ 91 more rows
## # ℹ 11 more variables: predator <lgl>, toothed <lgl>,
## #   backbone <lgl>, breathes <lgl>, venomous <lgl>,
## #   fins <lgl>, legs <int>, tail <lgl>, domestic <lgl>,
## #   catsize <lgl>, type <fct>

You will have to remove the animal column before learning a model! In the following I use the data.frame.

I translate all the TRUE/FALSE values into factors (nominal). This is often needed for building models. Always check summary() to make sure the data is ready for model learning.

Zoo <- Zoo |>
  mutate(across(where(is.logical), 
         function (x) factor(x, levels = c(TRUE, FALSE)))) |>
  mutate(across(where(is.character), factor))

summary(Zoo)
##     hair     feathers     eggs       milk     airborne 
##  TRUE :43   TRUE :20   TRUE :59   TRUE :41   TRUE :24  
##  FALSE:58   FALSE:81   FALSE:42   FALSE:60   FALSE:77  
##                                                        
##                                                        
##                                                        
##                                                        
##                                                        
##   aquatic    predator   toothed    backbone   breathes 
##  TRUE :36   TRUE :56   TRUE :61   TRUE :83   TRUE :80  
##  FALSE:65   FALSE:45   FALSE:40   FALSE:18   FALSE:21  
##                                                        
##                                                        
##                                                        
##                                                        
##                                                        
##   venomous     fins         legs         tail     domestic 
##  TRUE : 8   TRUE :17   Min.   :0.00   TRUE :75   TRUE :13  
##  FALSE:93   FALSE:84   1st Qu.:2.00   FALSE:26   FALSE:88  
##                        Median :4.00                        
##                        Mean   :2.84                        
##                        3rd Qu.:4.00                        
##                        Max.   :8.00                        
##                                                            
##   catsize              type   
##  TRUE :44   mammal       :41  
##  FALSE:57   bird         :20  
##             reptile      : 5  
##             fish         :13  
##             amphibian    : 4  
##             insect       : 8  
##             mollusc.et.al:10

3.3 Decision Tree Classifiers

We use here the recursive partitioning implementation (rpart) which follows largely CART and uses the Gini index to make splitting decisions and then it uses early stopping (also called pre-pruning).

library(rpart)

3.3.1 Create Tree

We create first a tree with the default settings (see ? rpart.control).

tree_default <- Zoo |> 
  rpart(type ~ ., data = _)
tree_default
## n= 101 
## 
## node), split, n, loss, yval, (yprob)
##       * denotes terminal node
## 
##  1) root 101 60 mammal (0.41 0.2 0.05 0.13 0.04 0.079 0.099)  
##    2) milk=TRUE 41  0 mammal (1 0 0 0 0 0 0) *
##    3) milk=FALSE 60 40 bird (0 0.33 0.083 0.22 0.067 0.13 0.17)  
##      6) feathers=TRUE 20  0 bird (0 1 0 0 0 0 0) *
##      7) feathers=FALSE 40 27 fish (0 0 0.12 0.33 0.1 0.2 0.25)  
##       14) fins=TRUE 13  0 fish (0 0 0 1 0 0 0) *
##       15) fins=FALSE 27 17 mollusc.et.al (0 0 0.19 0 0.15 0.3 0.37)  
##         30) backbone=TRUE 9  4 reptile (0 0 0.56 0 0.44 0 0) *
##         31) backbone=FALSE 18  8 mollusc.et.al (0 0 0 0 0 0.44 0.56) *

Notes:

|> supplies the data for rpart. Since data is not the first argument of rpart, the syntax data = _ is used to specify where the data in Zoo goes. The call is equivalent to tree_default <- rpart(type ~ ., data = Zoo).
The formula models the type variable by all other features represented by a single period (.).
The class variable needs to be a factor to be recognized as nominal or rpart will create a regression tree instead of a decision tree. Use as.factor() on the column with the class label first, if necessary.

We can plot the resulting decision tree.

library(rpart.plot)
rpart.plot(tree_default, extra = 2)

Note: extra=2 prints for each leaf node the number of correctly classified objects from data and the total number of objects from the training data falling into that node (correct/total).

3.3.2 Make Predictions for New Data

I will make up my own animal: A lion with feathered wings.

my_animal <- tibble(hair = TRUE, feathers = TRUE, eggs = FALSE,
  milk = TRUE, airborne = TRUE, aquatic = FALSE, predator = TRUE,
  toothed = TRUE, backbone = TRUE, breathes = TRUE, 
  venomous = FALSE, fins = FALSE, legs = 4, tail = TRUE, 
  domestic = FALSE, catsize = FALSE, type = NA)

The data types need to match the original data so we change the columns to be factors like in the training set.

my_animal <- my_animal |> 
  mutate(across(where(is.logical), 
                function(x) factor(x, levels = c(TRUE, FALSE))))
my_animal
## # A tibble: 1 × 17
##   hair  feathers eggs  milk  airborne aquatic predator
##   <fct> <fct>    <fct> <fct> <fct>    <fct>   <fct>   
## 1 TRUE  TRUE     FALSE TRUE  TRUE     FALSE   TRUE    
## # ℹ 10 more variables: toothed <fct>, backbone <fct>,
## #   breathes <fct>, venomous <fct>, fins <fct>, legs <dbl>,
## #   tail <fct>, domestic <fct>, catsize <fct>, type <fct>

Next, we make a prediction using the default tree

predict(tree_default , my_animal, type = "class")
##      1 
## mammal 
## 7 Levels: mammal bird reptile fish amphibian ... mollusc.et.al

3.3.3 Manual Calculation of the Resubstitution Error

We will calculate error of the model on the training data manually first, so we see how it is calculated.

predict(tree_default, Zoo) |> head ()
##          mammal bird reptile fish amphibian insect
## aardvark      1    0       0    0         0      0
## antelope      1    0       0    0         0      0
## bass          0    0       0    1         0      0
## bear          1    0       0    0         0      0
## boar          1    0       0    0         0      0
## buffalo       1    0       0    0         0      0
##          mollusc.et.al
## aardvark             0
## antelope             0
## bass                 0
## bear                 0
## boar                 0
## buffalo              0
pred <- predict(tree_default, Zoo, type="class")
head(pred)
## aardvark antelope     bass     bear     boar  buffalo 
##   mammal   mammal     fish   mammal   mammal   mammal 
## 7 Levels: mammal bird reptile fish amphibian ... mollusc.et.al

We can easily tabulate the true and predicted labels to create a confusion matrix.

confusion_table <- with(Zoo, table(type, pred))
confusion_table
##                pred
## type            mammal bird reptile fish amphibian insect
##   mammal            41    0       0    0         0      0
##   bird               0   20       0    0         0      0
##   reptile            0    0       5    0         0      0
##   fish               0    0       0   13         0      0
##   amphibian          0    0       4    0         0      0
##   insect             0    0       0    0         0      0
##   mollusc.et.al      0    0       0    0         0      0
##                pred
## type            mollusc.et.al
##   mammal                    0
##   bird                      0
##   reptile                   0
##   fish                      0
##   amphibian                 0
##   insect                    8
##   mollusc.et.al            10

The counts in the diagonal are correct predictions. Off-diagonal counts represent errors (i.e., confusions).

We can summarize the confusion matrix using the accuracy measure.

correct <- confusion_table |> diag() |> sum()
correct
## [1] 89
error <- confusion_table |> sum() - correct
error
## [1] 12
accuracy <- correct / (correct + error)
accuracy
## [1] 0.8812

Here is the accuracy calculation as a simple function.

accuracy <- function(truth, prediction) {
    tbl <- table(truth, prediction)
    sum(diag(tbl))/sum(tbl)
}

accuracy(Zoo |> pull(type), pred)
## [1] 0.8812

3.3.4 Confusion Matrix for the Resubstitution Error using Caret

The caret package provides a convenient way to create and analyze a confusion table including many useful statistics.

library(caret)
confusionMatrix(data = pred, 
                reference = Zoo |> pull(type))
## Confusion Matrix and Statistics
## 
##                Reference
## Prediction      mammal bird reptile fish amphibian insect
##   mammal            41    0       0    0         0      0
##   bird               0   20       0    0         0      0
##   reptile            0    0       5    0         4      0
##   fish               0    0       0   13         0      0
##   amphibian          0    0       0    0         0      0
##   insect             0    0       0    0         0      0
##   mollusc.et.al      0    0       0    0         0      8
##                Reference
## Prediction      mollusc.et.al
##   mammal                    0
##   bird                      0
##   reptile                   0
##   fish                      0
##   amphibian                 0
##   insect                    0
##   mollusc.et.al            10
## 
## Overall Statistics
##                                         
##                Accuracy : 0.881         
##                  95% CI : (0.802, 0.937)
##     No Information Rate : 0.406         
##     P-Value [Acc > NIR] : <2e-16        
##                                         
##                   Kappa : 0.843         
##                                         
##  Mcnemar's Test P-Value : NA            
## 
## Statistics by Class:
## 
##                      Class: mammal Class: bird
## Sensitivity                  1.000       1.000
## Specificity                  1.000       1.000
## Pos Pred Value               1.000       1.000
## Neg Pred Value               1.000       1.000
## Prevalence                   0.406       0.198
## Detection Rate               0.406       0.198
## Detection Prevalence         0.406       0.198
## Balanced Accuracy            1.000       1.000
##                      Class: reptile Class: fish
## Sensitivity                  1.0000       1.000
## Specificity                  0.9583       1.000
## Pos Pred Value               0.5556       1.000
## Neg Pred Value               1.0000       1.000
## Prevalence                   0.0495       0.129
## Detection Rate               0.0495       0.129
## Detection Prevalence         0.0891       0.129
## Balanced Accuracy            0.9792       1.000
##                      Class: amphibian Class: insect
## Sensitivity                    0.0000        0.0000
## Specificity                    1.0000        1.0000
## Pos Pred Value                    NaN           NaN
## Neg Pred Value                 0.9604        0.9208
## Prevalence                     0.0396        0.0792
## Detection Rate                 0.0000        0.0000
## Detection Prevalence           0.0000        0.0000
## Balanced Accuracy              0.5000        0.5000
##                      Class: mollusc.et.al
## Sensitivity                         1.000
## Specificity                         0.912
## Pos Pred Value                      0.556
## Neg Pred Value                      1.000
## Prevalence                          0.099
## Detection Rate                      0.099
## Detection Prevalence                0.178
## Balanced Accuracy                   0.956

Important note: Calculating accuracy on the training data is not a good idea. A complete example with code for holding out a test set and performing hyperparameter selection using cross-validation can be found in section Hyperparameter Tuning.

3.4 Model Overfitting

We are tempted to create the largest possible tree to get the most accurate model. This can be achieved by changing the algorithms hyperparameter (parameters that change how the algorithm works). We set the complexity parameter cp to 0 (split even if it does not improve the fit) and we set the minimum number of observations in a node needed to split to the smallest value of 2 (see: ?rpart.control). Note: This is not a good idea! As we will see later, full trees overfit the training data!

tree_full <- Zoo |> 
  rpart(type ~ . , data = _, 
        control = rpart.control(minsplit = 2, cp = 0))
rpart.plot(tree_full, extra = 2, 
           roundint=FALSE,
           box.palette = list("Gy", "Gn", "Bu", "Bn", 
                              "Or", "Rd", "Pu"))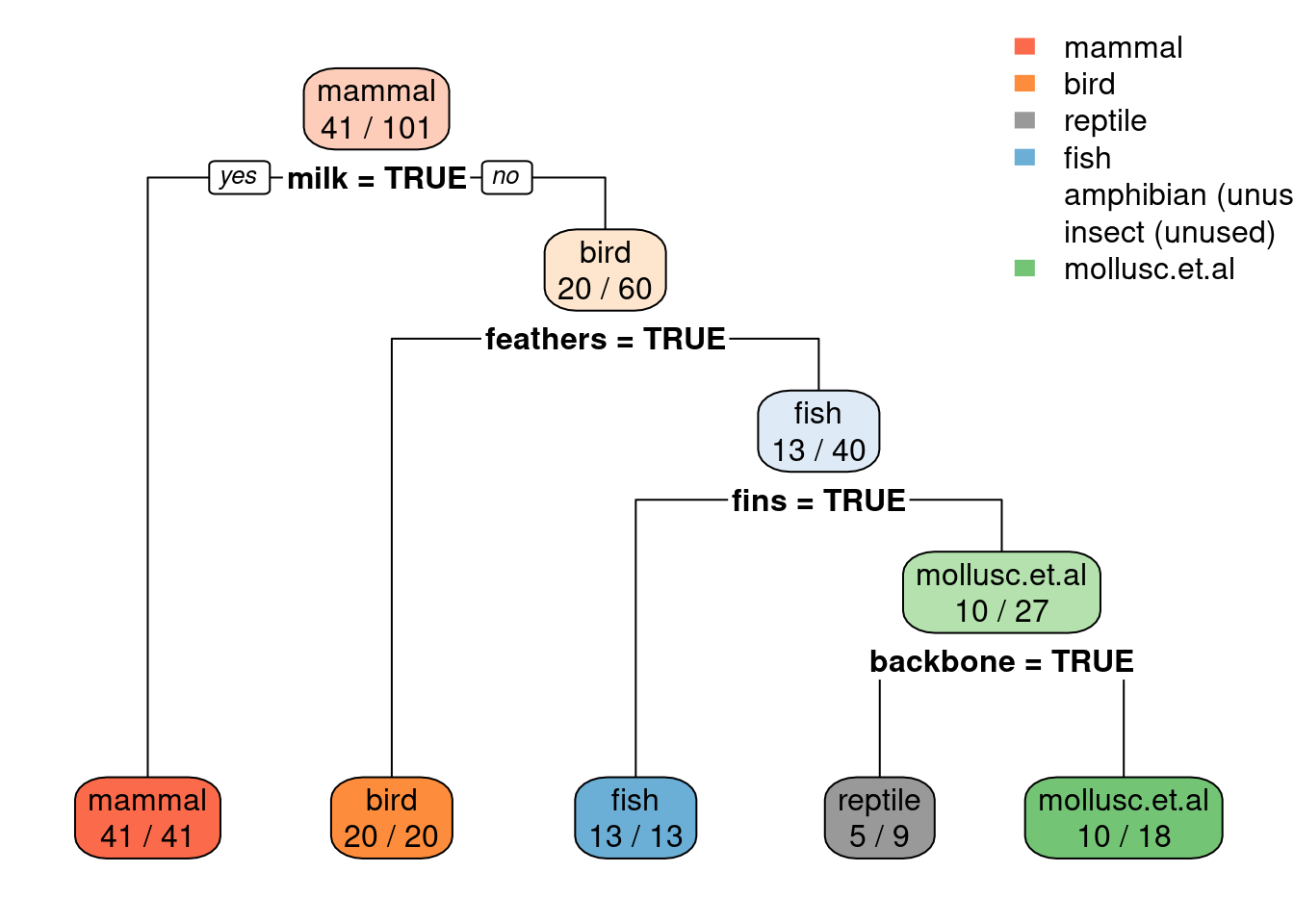

tree_full
## n= 101 
## 
## node), split, n, loss, yval, (yprob)
##       * denotes terminal node
## 
##   1) root 101 60 mammal (0.41 0.2 0.05 0.13 0.04 0.079 0.099)  
##     2) milk=TRUE 41  0 mammal (1 0 0 0 0 0 0) *
##     3) milk=FALSE 60 40 bird (0 0.33 0.083 0.22 0.067 0.13 0.17)  
##       6) feathers=TRUE 20  0 bird (0 1 0 0 0 0 0) *
##       7) feathers=FALSE 40 27 fish (0 0 0.12 0.33 0.1 0.2 0.25)  
##        14) fins=TRUE 13  0 fish (0 0 0 1 0 0 0) *
##        15) fins=FALSE 27 17 mollusc.et.al (0 0 0.19 0 0.15 0.3 0.37)  
##          30) backbone=TRUE 9  4 reptile (0 0 0.56 0 0.44 0 0)  
##            60) aquatic=FALSE 4  0 reptile (0 0 1 0 0 0 0) *
##            61) aquatic=TRUE 5  1 amphibian (0 0 0.2 0 0.8 0 0)  
##             122) eggs=FALSE 1  0 reptile (0 0 1 0 0 0 0) *
##             123) eggs=TRUE 4  0 amphibian (0 0 0 0 1 0 0) *
##          31) backbone=FALSE 18  8 mollusc.et.al (0 0 0 0 0 0.44 0.56)  
##            62) airborne=TRUE 6  0 insect (0 0 0 0 0 1 0) *
##            63) airborne=FALSE 12  2 mollusc.et.al (0 0 0 0 0 0.17 0.83)  
##             126) predator=FALSE 4  2 insect (0 0 0 0 0 0.5 0.5)  
##               252) legs>=3 2  0 insect (0 0 0 0 0 1 0) *
##               253) legs< 3 2  0 mollusc.et.al (0 0 0 0 0 0 1) *
##             127) predator=TRUE 8  0 mollusc.et.al (0 0 0 0 0 0 1) *

Error on the training set of the full tree

pred_full <- predict(tree_full, Zoo, type = "class")

accuracy(Zoo |> pull(type), pred_full)
## [1] 1

We see that the error is smaller then for the pruned tree. This, however, does not mean that the model is better. It actually is overfitting the training data (it just memorizes it) and it likely has worse generalization performance on new data. This effect is called overfitting the training data and needs to be avoided.

3.5 Model Selection

We often can create many different models for a classification problem. Above, we have created a decision tree using the default settings and also a full tree. The question is: Which one should we use. This problem is called model selection.

In order to select the model we need to split the training data into a validation set and the training set that is actually used to train model. The error rate on the validation set can then be used to choose between several models.

Caret has model selection build into the train() function. We will select between the default complexity cp = 0.01 and a full tree cp = 0 (set via tuneGrid). trControl specified how the validation set is obtained. We use Leave Group Out Cross-Validation (LGOCV) which picks randomly the proportion p of data to train and uses the rest as the validation set. To get a better estimate of the error, this process is repeated number of times and the errors are averaged.

fit <- Zoo |>
  train(type ~ .,
    data = _ ,
    method = "rpart",
    control = rpart.control(minsplit = 2), # we have little data
    tuneGrid = data.frame(cp = c(0.01, 0)),
    trControl = trainControl(method = "LGOCV", 
                             p = 0.8, 
                             number = 10),
    tuneLength = 5)

fit
## CART 
## 
## 101 samples
##  16 predictor
##   7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al' 
## 
## No pre-processing
## Resampling: Repeated Train/Test Splits Estimated (10 reps, 80%) 
## Summary of sample sizes: 83, 83, 83, 83, 83, 83, ... 
## Resampling results across tuning parameters:
## 
##   cp    Accuracy  Kappa 
##   0.00  0.9444    0.9232
##   0.01  0.9389    0.9155
## 
## Accuracy was used to select the optimal model using
##  the largest value.
## The final value used for the model was cp = 0.

We see that in this case, the full tree model performs slightly better. However, given the small dataset, this may not be a significant difference and we will look at a statistical test for this later.

3.6 Model Evaluation

Models should be evaluated on a test set that has no overlap with the training set. We typically split the data using random sampling. To get reproducible results, we set random number generator seed.

set.seed(2000)

3.6.1 Holdout Method

Test data is not used in the model building process and set aside purely for testing the model. Here, we partition data the 80% training and 20% testing.

inTrain <- createDataPartition(y = Zoo$type, p = .8)[[1]]
Zoo_train <- Zoo |> slice(inTrain)
Zoo_test <- Zoo |> slice(-inTrain)

Now we can train on the test set and get the generalization error on the test set.

3.6.2 Cross-Validation Methods

There are several cross-validation methods that can use the available datsa more efficiently then the holdout method. The most popular method is k-fold cross-validation which splits the data randomly into $k$ folds. It then holds one fold back for testing and trains on the other $k-1$ folds. This is done with each fold and the resulting statistic (e.g., accuracy) is averaged. This method uses the data more efficiently then the holdout method.

Cross validation can be directly used in train() using trControl = trainControl(method = "cv", number = 10). If no model selection is necessary then this will give the generalization error.

Cross-validation runs are independent and can be done faster in parallel. To enable multi-core support, caret uses the package foreach and you need to load a do backend. For Linux, you can use doMC with 4 cores. Windows needs different backend like doParallel (see caret cheat sheet above).

## Linux backend
# library(doMC)
# registerDoMC(cores = 4)
# getDoParWorkers()

## Windows backend
# library(doParallel)
# cl <- makeCluster(4, type="SOCK")
# registerDoParallel(cl)

3.7 Hyperparameter Tuning

Note: This section contains a complete code example of how data should be used. It first holds out a test set and then performing hyperparameter selection using cross-validation.

Hyperparameters are parameters that change how a training algorithm works. An example is the complexity parameter cp for rpart decision trees. Tuning the hyperparameter means that we want to perform model selection to pick the best setting.

We typically first use the holdout method to create a test set and then use cross validation using the training data for model selection. Let us use 80% for training and hold out 20% for testing.

inTrain <- createDataPartition(y = Zoo$type, p = .8)[[1]]
Zoo_train <- Zoo |> slice(inTrain)
Zoo_test <- Zoo |> slice(-inTrain)

The package caret combines training and validation for hyperparameter tuning into the train() function. It internally splits the data into training and validation sets and thus will provide you with error estimates for different hyperparameter settings. trainControl is used to choose how testing is performed.

For rpart, train tries to tune the cp parameter (tree complexity) using accuracy to chose the best model. I set minsplit to 2 since we have not much data. Note: Parameters used for tuning (in this case cp) need to be set using a data.frame in the argument tuneGrid! Setting it in control will be ignored.

fit <- Zoo_train |>
  train(type ~ .,
    data = _ ,
    method = "rpart",
    control = rpart.control(minsplit = 2), # we have little data
    trControl = trainControl(method = "cv", number = 10),
    tuneLength = 5)

fit
## CART 
## 
## 83 samples
## 16 predictors
##  7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 74, 73, 77, 75, 73, 75, ... 
## Resampling results across tuning parameters:
## 
##   cp    Accuracy  Kappa 
##   0.00  0.9289    0.9058
##   0.08  0.8603    0.8179
##   0.16  0.7296    0.6422
##   0.22  0.6644    0.5448
##   0.32  0.4383    0.1136
## 
## Accuracy was used to select the optimal model using
##  the largest value.
## The final value used for the model was cp = 0.

Note: Train has built 10 trees using the training folds for each value of cp and the reported values for accuracy and Kappa are the averages on the validation folds.

A model using the best tuning parameters and using all the data supplied to train() is available as fit$finalModel.

library(rpart.plot)
rpart.plot(fit$finalModel, extra = 2,
  box.palette = list("Gy", "Gn", "Bu", "Bn", "Or", "Rd", "Pu"))

caret also computes variable importance. By default it uses competing splits (splits which would be runners up, but do not get chosen by the tree) for rpart models (see ? varImp). Toothed is the runner up for many splits, but it never gets chosen!

varImp(fit)
## rpart variable importance
## 
##               Overall
## toothedFALSE    100.0
## feathersFALSE    79.5
## eggsFALSE        67.7
## milkFALSE        63.3
## backboneFALSE    57.3
## finsFALSE        53.5
## hairFALSE        52.1
## breathesFALSE    48.9
## legs             41.4
## tailFALSE        29.0
## aquaticFALSE     27.5
## airborneFALSE    26.5
## predatorFALSE    10.6
## venomousFALSE     1.8
## catsizeFALSE      0.0
## domesticFALSE     0.0

Here is the variable importance without competing splits.

imp <- varImp(fit, compete = FALSE)
imp
## rpart variable importance
## 
##               Overall
## milkFALSE      100.00
## feathersFALSE   55.69
## finsFALSE       39.45
## aquaticFALSE    28.11
## backboneFALSE   21.76
## eggsFALSE       12.32
## legs             7.28
## tailFALSE        0.00
## domesticFALSE    0.00
## airborneFALSE    0.00
## catsizeFALSE     0.00
## toothedFALSE     0.00
## venomousFALSE    0.00
## hairFALSE        0.00
## breathesFALSE    0.00
## predatorFALSE    0.00
ggplot(imp)

Note: Not all models provide a variable importance function. In this case caret might calculate the variable importance by itself and ignore the model (see ? varImp)!

Now, we can estimate the generalization error of the best model on the held out test data.

pred <- predict(fit, newdata = Zoo_test)
pred
##  [1] mammal        bird          mollusc.et.al bird         
##  [5] mammal        mammal        insect        bird         
##  [9] mammal        mammal        mammal        mammal       
## [13] bird          fish          fish          reptile      
## [17] mammal        mollusc.et.al
## 7 Levels: mammal bird reptile fish amphibian ... mollusc.et.al

Caret’s confusionMatrix() function calculates accuracy, confidence intervals, kappa and many more evaluation metrics. You need to use separate test data to create a confusion matrix based on the generalization error.

confusionMatrix(data = pred, 
                ref = Zoo_test |> pull(type))
## Confusion Matrix and Statistics
## 
##                Reference
## Prediction      mammal bird reptile fish amphibian insect
##   mammal             8    0       0    0         0      0
##   bird               0    4       0    0         0      0
##   reptile            0    0       1    0         0      0
##   fish               0    0       0    2         0      0
##   amphibian          0    0       0    0         0      0
##   insect             0    0       0    0         0      1
##   mollusc.et.al      0    0       0    0         0      0
##                Reference
## Prediction      mollusc.et.al
##   mammal                    0
##   bird                      0
##   reptile                   0
##   fish                      0
##   amphibian                 0
##   insect                    0
##   mollusc.et.al             2
## 
## Overall Statistics
##                                     
##                Accuracy : 1         
##                  95% CI : (0.815, 1)
##     No Information Rate : 0.444     
##     P-Value [Acc > NIR] : 4.58e-07  
##                                     
##                   Kappa : 1         
##                                     
##  Mcnemar's Test P-Value : NA        
## 
## Statistics by Class:
## 
##                      Class: mammal Class: bird
## Sensitivity                  1.000       1.000
## Specificity                  1.000       1.000
## Pos Pred Value               1.000       1.000
## Neg Pred Value               1.000       1.000
## Prevalence                   0.444       0.222
## Detection Rate               0.444       0.222
## Detection Prevalence         0.444       0.222
## Balanced Accuracy            1.000       1.000
##                      Class: reptile Class: fish
## Sensitivity                  1.0000       1.000
## Specificity                  1.0000       1.000
## Pos Pred Value               1.0000       1.000
## Neg Pred Value               1.0000       1.000
## Prevalence                   0.0556       0.111
## Detection Rate               0.0556       0.111
## Detection Prevalence         0.0556       0.111
## Balanced Accuracy            1.0000       1.000
##                      Class: amphibian Class: insect
## Sensitivity                        NA        1.0000
## Specificity                         1        1.0000
## Pos Pred Value                     NA        1.0000
## Neg Pred Value                     NA        1.0000
## Prevalence                          0        0.0556
## Detection Rate                      0        0.0556
## Detection Prevalence                0        0.0556
## Balanced Accuracy                  NA        1.0000
##                      Class: mollusc.et.al
## Sensitivity                         1.000
## Specificity                         1.000
## Pos Pred Value                      1.000
## Neg Pred Value                      1.000
## Prevalence                          0.111
## Detection Rate                      0.111
## Detection Prevalence                0.111
## Balanced Accuracy                   1.000

Some notes

Many classification algorithms and train in caret do not deal well with missing values. If your classification model can deal with missing values (e.g., rpart) then use na.action = na.pass when you call train and predict. Otherwise, you need to remove observations with missing values with na.omit or use imputation to replace the missing values before you train the model. Make sure that you still have enough observations left.
Make sure that nominal variables (this includes logical variables) are coded as factors.
The class variable for train in caret cannot have level names that are keywords in R (e.g., TRUE and FALSE). Rename them to, for example, “yes” and “no.”
Make sure that nominal variables (factors) have examples for all possible values. Some methods might have problems with variable values without examples. You can drop empty levels using droplevels or factor.
Sampling in train might create a sample that does not contain examples for all values in a nominal (factor) variable. You will get an error message. This most likely happens for variables which have one very rare value. You may have to remove the variable.

3.8 Pitfalls of Model Selection and Evaluation

Do not measure the error on the training set or use the validation error as a generalization error estimate. Always use the generalization error on a test set!
The training data and the test sets cannot overlap or we will not evaluate the generalization performance. The training set can be come contaminated by things like preprocessing the all the data together.

3.9 Model Comparison

We will compare three models, a majority class baseline classifier, a decision trees with a k-nearest neighbors (kNN) classifier. We will use 10-fold cross-validation for hyper parameter tuning. Caret’s train() function refits the selected model on all of the training data and performs cross-validation to estimate the generalization error. These cross-validation results can be used to compare models statistically.

3.9.1 Build models

Caret does not provide a baseline classifier, but the package basemodels does. We first create a weak baseline model that always predicts the the majority class mammal.

baseline <- Zoo_train |> train(type ~ .,
  method = basemodels::dummyClassifier,
  data = _,
  strategy = "constant",
  constant = "mammal",
  trControl = trainControl(method = "cv" 
                           ))
baseline
## dummyClassifier 
## 
## 83 samples
## 16 predictors
##  7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 73, 74, 73, 75, 74, 77, ... 
## Resampling results:
## 
##   Accuracy  Kappa
##   0.4047    0

The second model is a default decision tree.

rpartFit <- Zoo_train |> 
  train(type ~ .,
        data = _,
        method = "rpart",
        tuneLength = 10,
        trControl = trainControl(method = "cv")
  )
rpartFit
## CART 
## 
## 83 samples
## 16 predictors
##  7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 75, 75, 75, 73, 76, 72, ... 
## Resampling results across tuning parameters:
## 
##   cp       Accuracy  Kappa 
##   0.00000  0.7841    0.7195
##   0.03556  0.7841    0.7195
##   0.07111  0.7841    0.7195
##   0.10667  0.7841    0.7182
##   0.14222  0.7841    0.7182
##   0.17778  0.7271    0.6369
##   0.21333  0.7071    0.6109
##   0.24889  0.5940    0.4423
##   0.28444  0.5940    0.4423
##   0.32000  0.4968    0.2356
## 
## Accuracy was used to select the optimal model using
##  the largest value.
## The final value used for the model was cp = 0.1422.

The third model is a kNN classifier, this classifier will be discussed in the next Chapter. kNN uses the Euclidean distance between objects. Logicals will be used as 0-1 variables. To make sure the range of all variables is compatible, we ask train to scale the data using preProcess = "scale".

knnFit <- Zoo_train |> 
  train(type ~ .,
        data = _,
        method = "knn",
        preProcess = "scale",
          tuneLength = 10,
          trControl = trainControl(method = "cv")
  )
knnFit
## k-Nearest Neighbors 
## 
## 83 samples
## 16 predictors
##  7 classes: 'mammal', 'bird', 'reptile', 'fish', 'amphibian', 'insect', 'mollusc.et.al' 
## 
## Pre-processing: scaled (16) 
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 75, 74, 74, 74, 74, 75, ... 
## Resampling results across tuning parameters:
## 
##   k   Accuracy  Kappa 
##    5  0.9092    0.8835
##    7  0.8715    0.8301
##    9  0.8579    0.8113
##   11  0.8590    0.8131
##   13  0.8727    0.8302
##   15  0.8727    0.8302
##   17  0.8490    0.7989
##   19  0.8490    0.7967
##   21  0.7943    0.7219
##   23  0.7943    0.7217
## 
## Accuracy was used to select the optimal model using
##  the largest value.
## The final value used for the model was k = 5.

Compare the accuracy and kappa distributions of the final model over all folds.

resamps <- resamples(list(
    baseline = baseline,    
  CART = rpartFit,
        kNearestNeighbors = knnFit
        ))

summary(resamps)
## 
## Call:
## summary.resamples(object = resamps)
## 
## Models: baseline, CART, kNearestNeighbors 
## Number of resamples: 10 
## 
## Accuracy 
##                     Min. 1st Qu. Median   Mean 3rd Qu.
## baseline          0.3000   0.375 0.3875 0.4047  0.4444
## CART              0.7143   0.733 0.7639 0.7841  0.8429
## kNearestNeighbors 0.7778   0.875 0.8819 0.9092  1.0000
##                    Max. NA's
## baseline          0.500    0
## CART              0.875    0
## kNearestNeighbors 1.000    0
## 
## Kappa 
##                     Min. 1st Qu. Median   Mean 3rd Qu.
## baseline          0.0000  0.0000 0.0000 0.0000  0.0000
## CART              0.6316  0.6622 0.6994 0.7182  0.7917
## kNearestNeighbors 0.7188  0.8307 0.8486 0.8835  1.0000
##                    Max. NA's
## baseline          0.000    0
## CART              0.814    0
## kNearestNeighbors 1.000    0

caret provides some visualizations. For example, a boxplot to compare the accuracy and kappa distribution (over the 10 folds).

bwplot(resamps, layout = c(3, 1))

We see that the baseline has no predictive power and produces consistently a kappa of 0. KNN performs consistently the best. To find out if one models is statistically better than the other, we can use a statistical test.

difs <- diff(resamps)
difs
## 
## Call:
## diff.resamples(x = resamps)
## 
## Models: baseline, CART, kNearestNeighbors 
## Metrics: Accuracy, Kappa 
## Number of differences: 3 
## p-value adjustment: bonferroni
summary(difs)
## 
## Call:
## summary.diff.resamples(object = difs)
## 
## p-value adjustment: bonferroni 
## Upper diagonal: estimates of the difference
## Lower diagonal: p-value for H0: difference = 0
## 
## Accuracy 
##                   baseline CART   kNearestNeighbors
## baseline                   -0.379 -0.504           
## CART              5.19e-06        -0.125           
## kNearestNeighbors 4.03e-08 0.031                   
## 
## Kappa 
##                   baseline CART   kNearestNeighbors
## baseline                   -0.718 -0.884           
## CART              5.79e-10        -0.165           
## kNearestNeighbors 2.87e-09 0.0206

p-values gives us the probability of seeing an even more extreme value (difference between accuracy or kappa) given that the null hypothesis (difference = 0) is true. For a better classifier, the p-value should be “significant,” i.e., less than .05 or 0.01. diff automatically applies Bonferroni correction for multiple comparisons to adjust the p-value upwards. In this case, CART and kNN perform significantly better than the baseline classifiers. The difference between CART and kNN is only significant at the 0.05 level, so kNN might be slightly better.

3.10 Feature Selection*

Decision trees implicitly select features for splitting, but we can also select features before we apply any learning algorithm. Since different features lead to different models, choosing the best set of features is also a type of model selection.

Many feature selection methods are implemented in the FSelector package.

library(FSelector)

3.10.1 Univariate Feature Importance Score

These scores measure how related each feature is to the class variable. For discrete features (as in our case), the chi-square statistic can be used to derive a score.

weights <- Zoo_train |> 
  chi.squared(type ~ ., data = _) |>
  as_tibble(rownames = "feature") |>
  arrange(desc(attr_importance))

weights
## # A tibble: 16 × 2
##    feature  attr_importance
##    <chr>              <dbl>
##  1 feathers           1    
##  2 milk               1    
##  3 backbone           1    
##  4 toothed            0.981
##  5 eggs               0.959
##  6 breathes           0.917
##  7 hair               0.906
##  8 fins               0.845
##  9 legs               0.834
## 10 airborne           0.818
## 11 tail               0.779
## 12 aquatic            0.725
## 13 catsize            0.602
## 14 venomous           0.520
## 15 predator           0.374
## 16 domestic           0.256

We can plot the importance in descending order (using reorder to order factor levels used by ggplot).

ggplot(weights,
  aes(x = attr_importance, 
      y = reorder(feature, attr_importance))) +
  geom_bar(stat = "identity") +
  xlab("Importance score") + 
  ylab("Feature")

Picking the best features is called the feature ranking approach. Here we pick the 5 highest-ranked features.

subset <- cutoff.k(weights |> 
                   column_to_rownames("feature"), 
                   5)
subset
## [1] "feathers" "milk"     "backbone" "toothed"  "eggs"

Use only the selected features to build a model (Fselector provides as.simple.formula).

f <- as.simple.formula(subset, "type")
f
## type ~ feathers + milk + backbone + toothed + eggs
## <environment: 0x637e4f7b2a08>
m <- Zoo_train |> rpart(f, data = _)
rpart.plot(m, extra = 2, roundint = FALSE)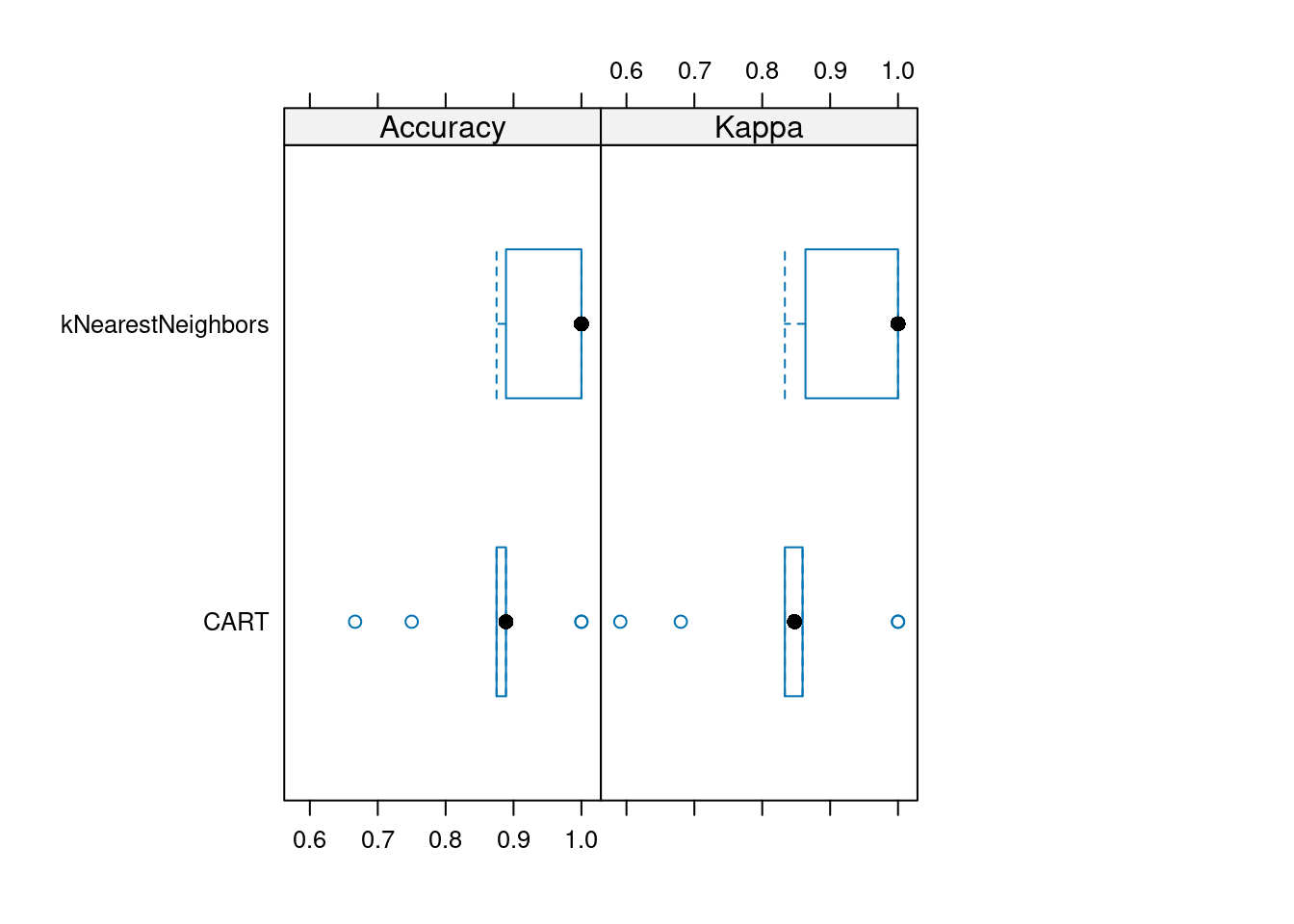

There are many alternative ways to calculate univariate importance scores (see package FSelector). Some of them (also) work for continuous features. One example is the information gain ratio based on entropy as used in decision tree induction.

Zoo_train |> 
  gain.ratio(type ~ ., data = _) |>
  as_tibble(rownames = "feature") |>
  arrange(desc(attr_importance))
## # A tibble: 16 × 2
##    feature  attr_importance
##    <chr>              <dbl>
##  1 milk               1    
##  2 backbone           1    
##  3 feathers           1    
##  4 toothed            0.959
##  5 eggs               0.907
##  6 breathes           0.845
##  7 hair               0.781
##  8 fins               0.689
##  9 legs               0.689
## 10 airborne           0.633
## 11 tail               0.573
## 12 aquatic            0.474
## 13 venomous           0.429
## 14 catsize            0.310
## 15 domestic           0.115
## 16 predator           0.110

3.10.2 Feature Subset Selection

Often, features are related and calculating importance for each feature independently is not optimal. We can use greedy search heuristics. For example cfs uses correlation/entropy with best first search.

Zoo_train |> 
  cfs(type ~ ., data = _)
##  [1] "hair"     "feathers" "eggs"     "milk"     "toothed" 
##  [6] "backbone" "breathes" "fins"     "legs"     "tail"

The disadvantage of this method is that the model we want to train may not use correlation/entropy. We can use the actual model using as a black-box defined in an evaluator function to calculate a score to be maximized. This is typically the best method, since it can use the model for selection. First, we define an evaluation function that builds a model given a subset of features and calculates a quality score. We use here the average for 5 bootstrap samples (method = "cv" can also be used instead), no tuning (to be faster), and the average accuracy as the score.

evaluator <- function(subset) {
  model <- Zoo_train |> 
    train(as.simple.formula(subset, "type"),
          data = _,
          method = "rpart",
          trControl = trainControl(method = "boot", number = 5),
          tuneLength = 0)
  
  results <- model$resample$Accuracy
  
  cat("Trying features:", paste(subset, collapse = " + "), "\n")
  
  m <- mean(results)
  cat("Accuracy:", round(m, 2), "\n\n")
  m
}

Start with all features (but not the class variable type)

features <- Zoo_train |> 
  colnames() |> 
  setdiff("type")

There are several (greedy) search strategies available. These run for a while so they commented out below. Remove the comment for one at a time to try these types of feature selection.

#subset <- backward.search(features, evaluator)
#subset <- forward.search(features, evaluator)
#subset <- best.first.search(features, evaluator)
#subset <- hill.climbing.search(features, evaluator)
#subset

3.10.3 Using Dummy Variables for Factors

Nominal features (factors) are often encoded as a series of 0-1 dummy variables. For example, let us try to predict if an animal is a predator given the type. First we use the original encoding of type as a factor with several values.

tree_predator <- Zoo_train |> 
  rpart(predator ~ type, data = _)
rpart.plot(tree_predator, extra = 2, roundint = FALSE)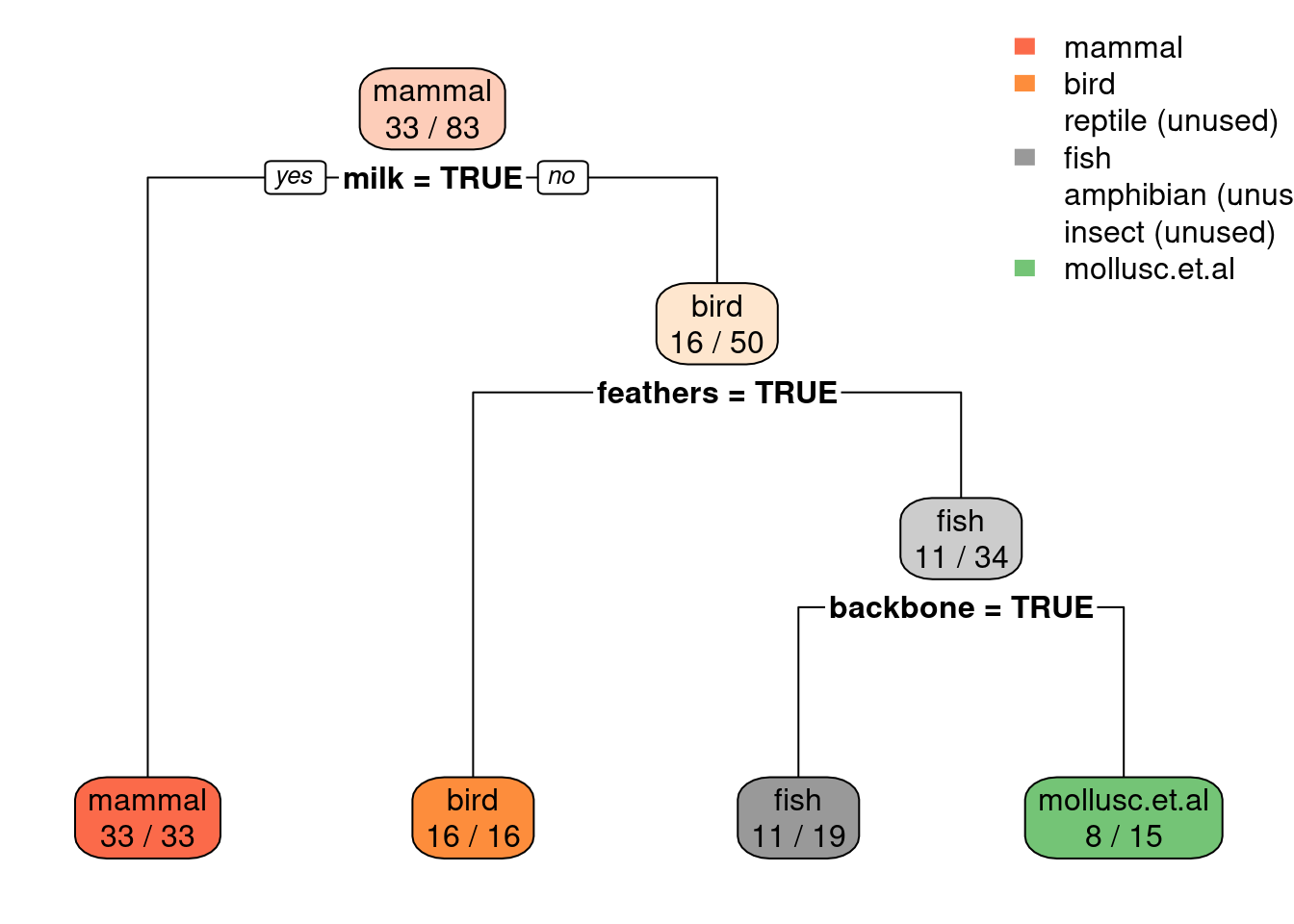

Note: Some splits use multiple values. Building the tree will become extremely slow if a factor has many levels (different values) since the tree has to check all possible splits into two subsets. This situation should be avoided.

Convert type into a set of 0-1 dummy variables using class2ind. See also ? dummyVars in package caret.

Zoo_train_dummy <- as_tibble(class2ind(Zoo_train$type)) |> 
  mutate(across(everything(), as.factor)) |>
  add_column(predator = Zoo_train$predator)
Zoo_train_dummy
## # A tibble: 83 × 8
##    mammal bird  reptile fish  amphibian insect mollusc.et.al
##    <fct>  <fct> <fct>   <fct> <fct>     <fct>  <fct>        
##  1 1      0     0       0     0         0      0            
##  2 0      0     0       1     0         0      0            
##  3 1      0     0       0     0         0      0            
##  4 1      0     0       0     0         0      0            
##  5 1      0     0       0     0         0      0            
##  6 1      0     0       0     0         0      0            
##  7 0      0     0       1     0         0      0            
##  8 0      0     0       1     0         0      0            
##  9 1      0     0       0     0         0      0            
## 10 1      0     0       0     0         0      0            
## # ℹ 73 more rows
## # ℹ 1 more variable: predator <fct>
tree_predator <- Zoo_train_dummy |> 
  rpart(predator ~ ., 
        data = _,
        control = rpart.control(minsplit = 2, cp = 0.01))
rpart.plot(tree_predator, roundint = FALSE)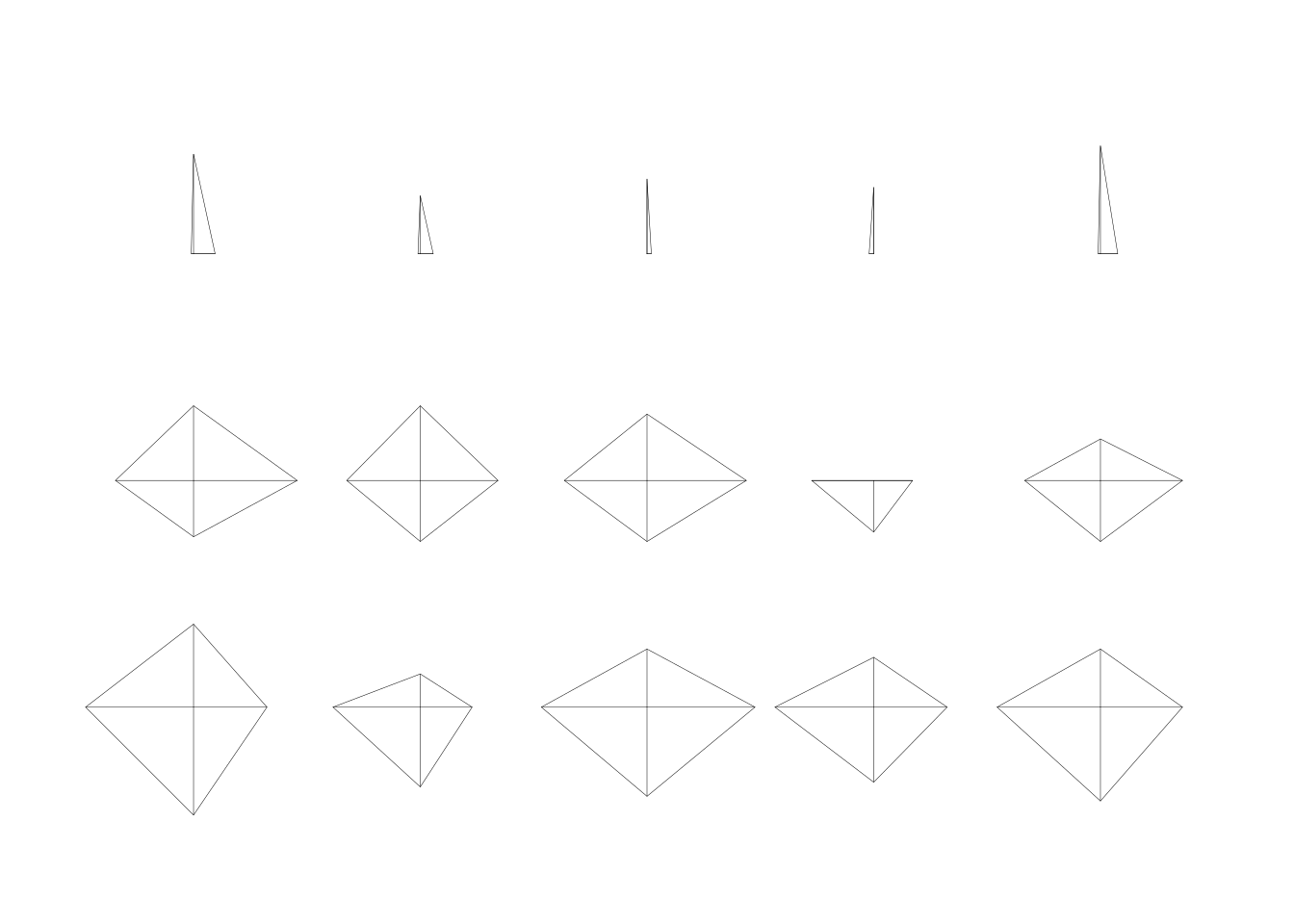

Using caret on the original factor encoding automatically translates factors (here type) into 0-1 dummy variables (e.g., typeinsect = 0). The reason is that some models cannot directly use factors and caret tries to consistently work with all of them.

fit <- Zoo_train |> 
  train(predator ~ type, 
        data = _, 
        method = "rpart",
        control = rpart.control(minsplit = 2),
        tuneGrid = data.frame(cp = 0.01))
fit
## CART 
## 
## 83 samples
##  1 predictor
##  2 classes: 'TRUE', 'FALSE' 
## 
## No pre-processing
## Resampling: Bootstrapped (25 reps) 
## Summary of sample sizes: 83, 83, 83, 83, 83, 83, ... 
## Resampling results:
## 
##   Accuracy  Kappa  
##   0.54      0.07527
## 
## Tuning parameter 'cp' was held constant at a value of 0.01
rpart.plot(fit$finalModel, extra = 2)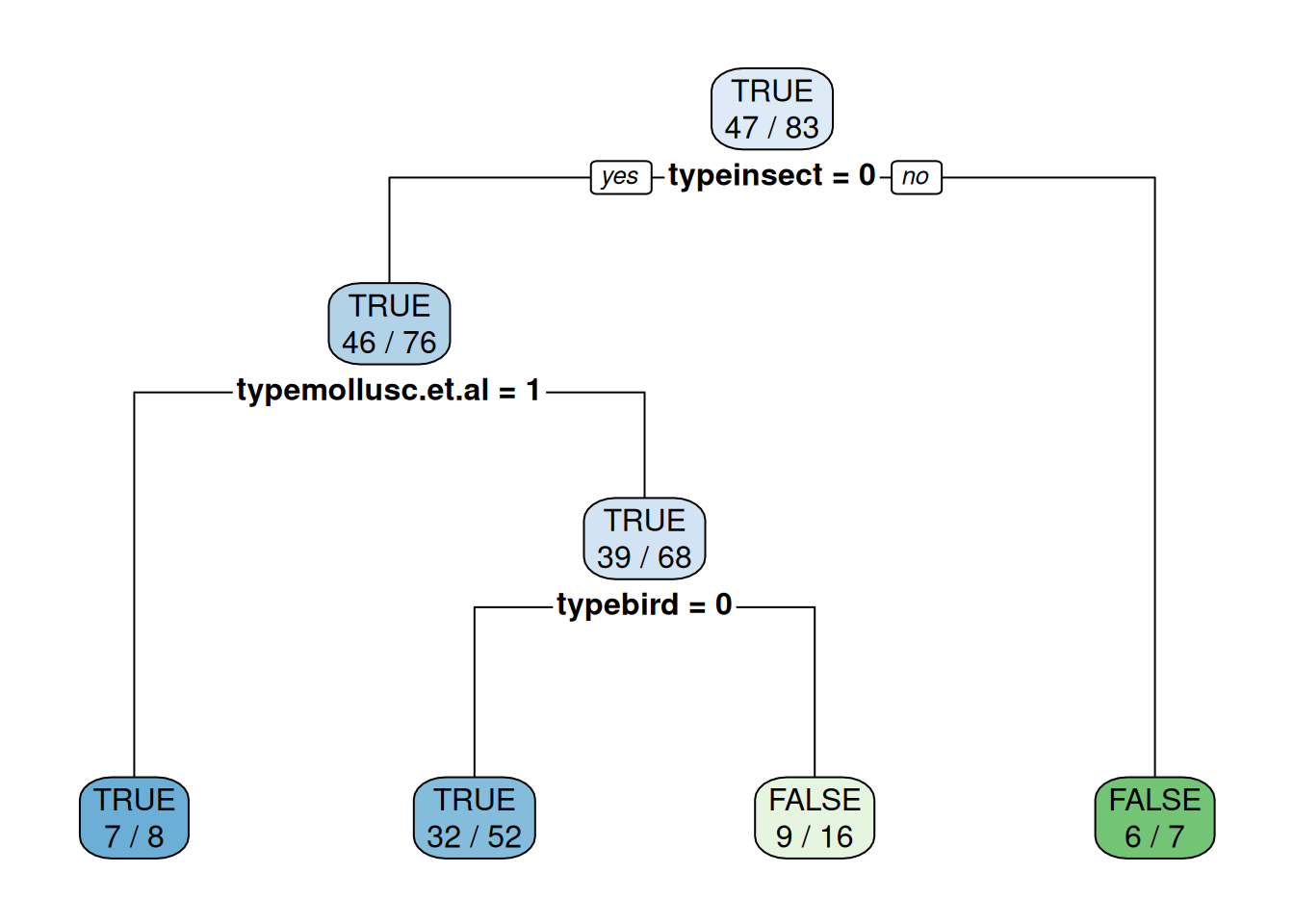

Note: To use a fixed value for the tuning parameter cp, we have to create a tuning grid that only contains that value.

3.11 Exercises*

We will use again the Palmer penguin data for the exercises.

library(palmerpenguins)
head(penguins)
## # A tibble: 6 × 8
##   species island    bill_length_mm bill_depth_mm
##   <chr>   <chr>              <dbl>         <dbl>
## 1 Adelie  Torgersen           39.1          18.7
## 2 Adelie  Torgersen           39.5          17.4
## 3 Adelie  Torgersen           40.3          18  
## 4 Adelie  Torgersen           NA            NA  
## 5 Adelie  Torgersen           36.7          19.3
## 6 Adelie  Torgersen           39.3          20.6
## # ℹ 4 more variables: flipper_length_mm <dbl>,
## #   body_mass_g <dbl>, sex <chr>, year <dbl>

Create a R markdown file with the code and discussion for the following below. Remember, the complete approach is described in section Hyperparameter Tuning.

Split the data into a training and test set.
Create an rpart decision tree to predict the species. You will have to deal with missing values.
Experiment with setting minsplit for rpart and make sure tuneLength is at least 5. Discuss the model selection process (hyperparameter tuning) and what final model was chosen.
Visualize the tree and discuss what the splits mean.
Calculate the variable importance from the fitted model. What variables are the most important? What variables do not matter?
Use the test set to evaluate the generalization error and accuracy.

2 Data

4 Classification: Alternative Techniques