B Regression
Regression is an important statistical method that is covered the freely available Appendix D of the data mining textbook.
In this extra chapter, we introduce the regression problem and multiple linear regression. In addition, alternative models like regression trees and regularized regression are discussed.
Packages Used in this Chapter
pkgs <- c('lars', 'rpart', 'rpart.plot')
pkgs_install <- pkgs[!(pkgs %in% installed.packages()[,"Package"])]
if(length(pkgs_install)) install.packages(pkgs_install)The packages used for this chapter are:
- lars (Hastie and Efron 2022)
- rpart (Therneau and Atkinson 2025)
- rpart.plot (Milborrow 2024)
B.1 Introduction
Recall that classification predicts one of a small set of discrete (i.e., nominal) labels (e.g., yes or no, small, medium or large). Regression is also a supervised learning problem, but the goal is to predict the value of a continuous value given a set of predictors. We start with the popular linear regression and will later discuss alternative regression methods.
Linear regression models the value of a dependent variable \(y\) (also called the response) as as linear function of independent variables \(X_1, X_2, ..., X_p\) (also called the regressors, predictors, exogenous variables, explanatory variables, or covariates). If we use more than one explanatory variable, then we often call this multiple or multivariate linear regression. The linear regression model is: \[\hat{y}_i = f(\mathbf{x}_i) = \beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip} + \epsilon_i = \beta_0 + \sum_{j = 1}^p{\left(\beta_jx_{ij}\right) + \epsilon_i},\]
where \(\beta_0\) is the intercept, \(\boldsymbol{\beta}\) is a \(p+1\)-dimensional parameter vector learned from the data, and \(\epsilon\) is the error term (called the residuals). This is often also written in vector notation as \[\hat{\mathbf{y}} = \mathbf{X} \boldsymbol{\beta} + \epsilon,\] where \(\hat{\mathbf{y}}\) and \(\boldsymbol{\beta}\) are vectors and \(\mathbf{X}\) is the matrix with the covariates (called the design matrix).
The error that is often minimized in regression problems is the squared error defined as:
\[SE= \sum_i (y_i - f(\mathbf{x}_i))^2\]
The parameter vector is found by minimizing the squared error the training data.
Linear regression makes several assumptions that should be checked:
- Linearity: There is a linear relationship between dependent and independent variables.
- Homoscedasticity: The variance of the error (\(\epsilon\)) does not change (increase) with the predicted value.
- Independence of errors: Errors between observations are uncorrelated.
- No multicollinearity of predictors: Predictors cannot be perfectly correlated or the parameter vector cannot be identified. Note that highly correlated predictors lead to unstable results and should be avoided using, e.g., variable selection.
B.2 A First Linear Regression Model
We will use the Iris dataset and try to predict
the Petal.Width using the other variables. We first
load and shuffle data since the flowers in the dataset are in order by species.
data(iris)
set.seed(2000) # make the sampling reproducible
x <- iris[sample(1:nrow(iris)),]
plot(x, col=x$Species)
The Iris data is very clean, so we make the data a little messy by adding a random error to each variable and introduce a useless, completely random feature.
x[,1] <- x[,1] + rnorm(nrow(x))
x[,2] <- x[,2] + rnorm(nrow(x))
x[,3] <- x[,3] + rnorm(nrow(x))
x <- cbind(x[,-5],
useless = mean(x[,1]) + rnorm(nrow(x)),
Species = x[,5])
plot(x, col=x$Species)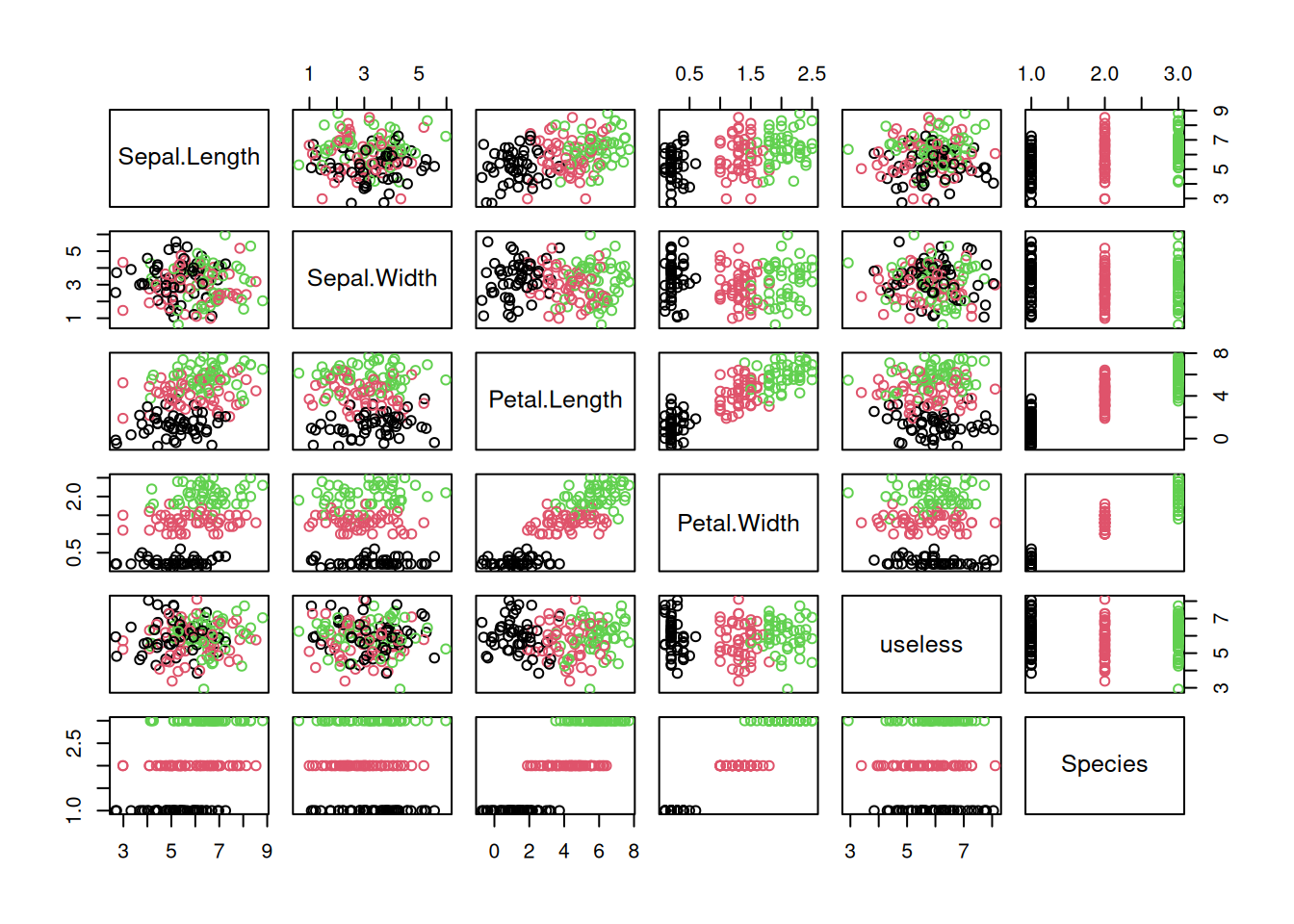
summary(x)
## Sepal.Length Sepal.Width Petal.Length
## Min. :2.68 Min. :0.611 Min. :-0.713
## 1st Qu.:5.05 1st Qu.:2.306 1st Qu.: 1.876
## Median :5.92 Median :3.171 Median : 4.102
## Mean :5.85 Mean :3.128 Mean : 3.781
## 3rd Qu.:6.70 3rd Qu.:3.945 3rd Qu.: 5.546
## Max. :8.81 Max. :5.975 Max. : 7.708
## Petal.Width useless Species
## Min. :0.1 Min. :2.92 setosa :50
## 1st Qu.:0.3 1st Qu.:5.23 versicolor:50
## Median :1.3 Median :5.91 virginica :50
## Mean :1.2 Mean :5.88
## 3rd Qu.:1.8 3rd Qu.:6.57
## Max. :2.5 Max. :8.11
head(x)
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 85 2.980 1.464 5.227 1.5
## 104 5.096 3.044 5.187 1.8
## 30 4.361 2.832 1.861 0.2
## 53 8.125 2.406 5.526 1.5
## 143 6.372 1.565 6.147 1.9
## 142 6.526 3.697 5.708 2.3
## useless Species
## 85 5.712 versicolor
## 104 6.569 virginica
## 30 4.299 setosa
## 53 6.124 versicolor
## 143 6.553 virginica
## 142 5.222 virginicaWe split the data into training and test data. Since the data is shuffled, we effectively perform holdout sampling. This is often not done in statistical applications, but we use the machine learning approach here.
train <- x[1:100,]
test <- x[101:150,]Linear regression is done in R using the lm() (linear model) function which is
part of the R core package stats.
Like other modeling functions in R, lm() uses a formula interface. Here we create a formula
to predict Petal.Width by all other variables other than Species.
model1 <- lm(Petal.Width ~ Sepal.Length
+ Sepal.Width + Petal.Length + useless,
data = train)
model1
##
## Call:
## lm(formula = Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length +
## useless, data = train)
##
## Coefficients:
## (Intercept) Sepal.Length Sepal.Width Petal.Length
## -0.20589 0.01957 0.03406 0.30814
## useless
## 0.00392The result is a model with the fitted \(\beta\) coefficients. More information can be displayed using the summary function.
summary(model1)
##
## Call:
## lm(formula = Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length +
## useless, data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.0495 -0.2033 0.0074 0.2038 0.8564
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.20589 0.28723 -0.72 0.48
## Sepal.Length 0.01957 0.03265 0.60 0.55
## Sepal.Width 0.03406 0.03549 0.96 0.34
## Petal.Length 0.30814 0.01819 16.94 <2e-16 ***
## useless 0.00392 0.03558 0.11 0.91
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.366 on 95 degrees of freedom
## Multiple R-squared: 0.778, Adjusted R-squared: 0.769
## F-statistic: 83.4 on 4 and 95 DF, p-value: <2e-16The summary shows:
- Which coefficients are significantly different from 0. Here only
Petal.Lengthis significant and the coefficient foruselessis very close to 0. Look at the scatter plot matrix above and see why this is the case. - R-squared (coefficient of determination): Proportion (in the range \([0,1]\)) of the variability of the dependent variable explained by the model. It is better to look at the adjusted R-square (adjusted for number of dependent variables). Typically, an R-squared of greater than \(0.7\) is considered good, but this is just a rule of thumb and we should rather use a test set for evaluation.
Plotting the model produces diagnostic plots (see plot.lm()). For example,
to check that the error term has a mean of 0 and is homoscedastic,
the residual vs. predicted value scatter plot
should have a red line that stays clode to 0 and
not look like a funnel where they are increasing when the fitted values increase.
To check if the residuals are approximately normally distributed,
the Q-Q plot should be close to the straight diagonal line.
plot(model1, which = 1:2)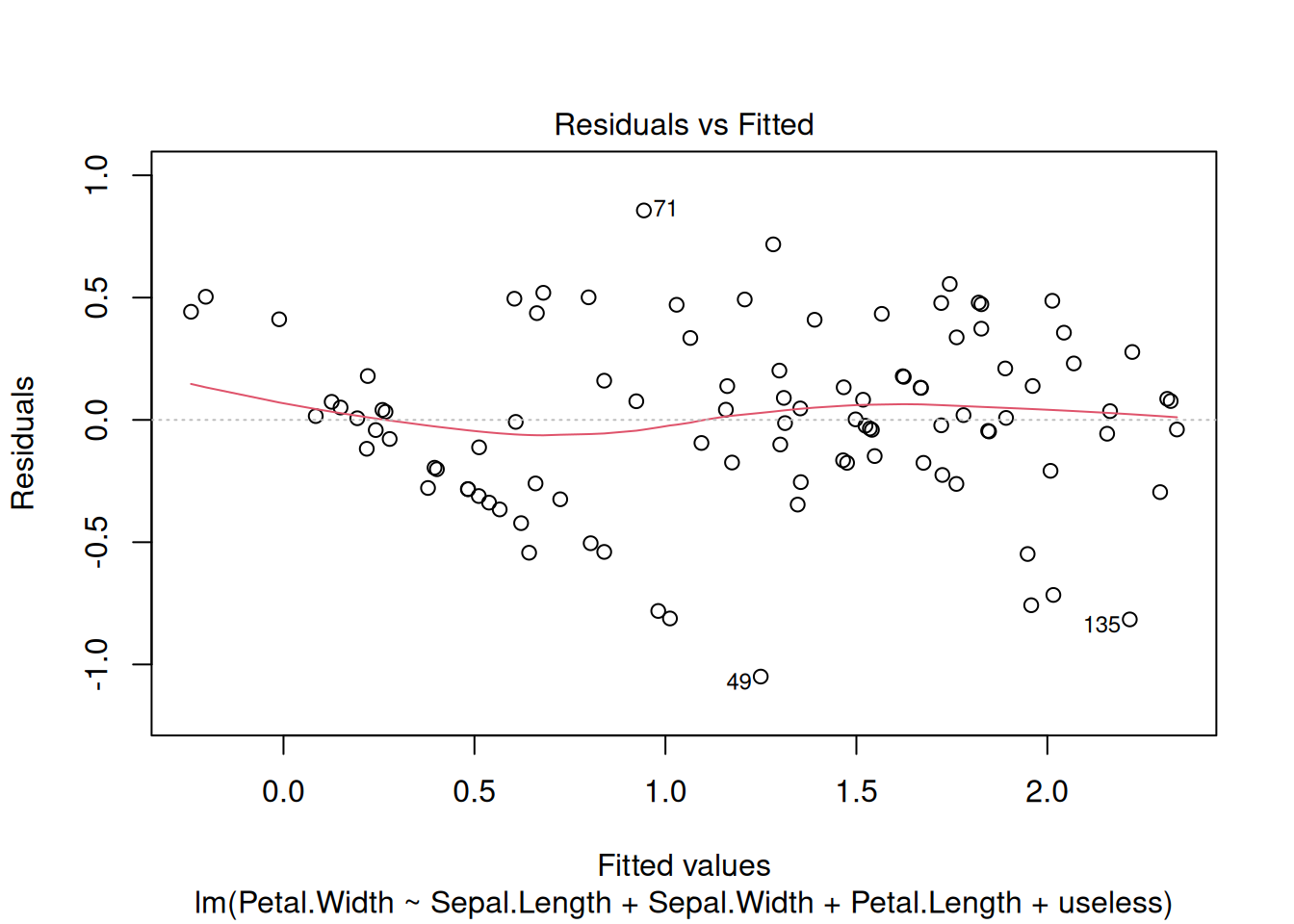
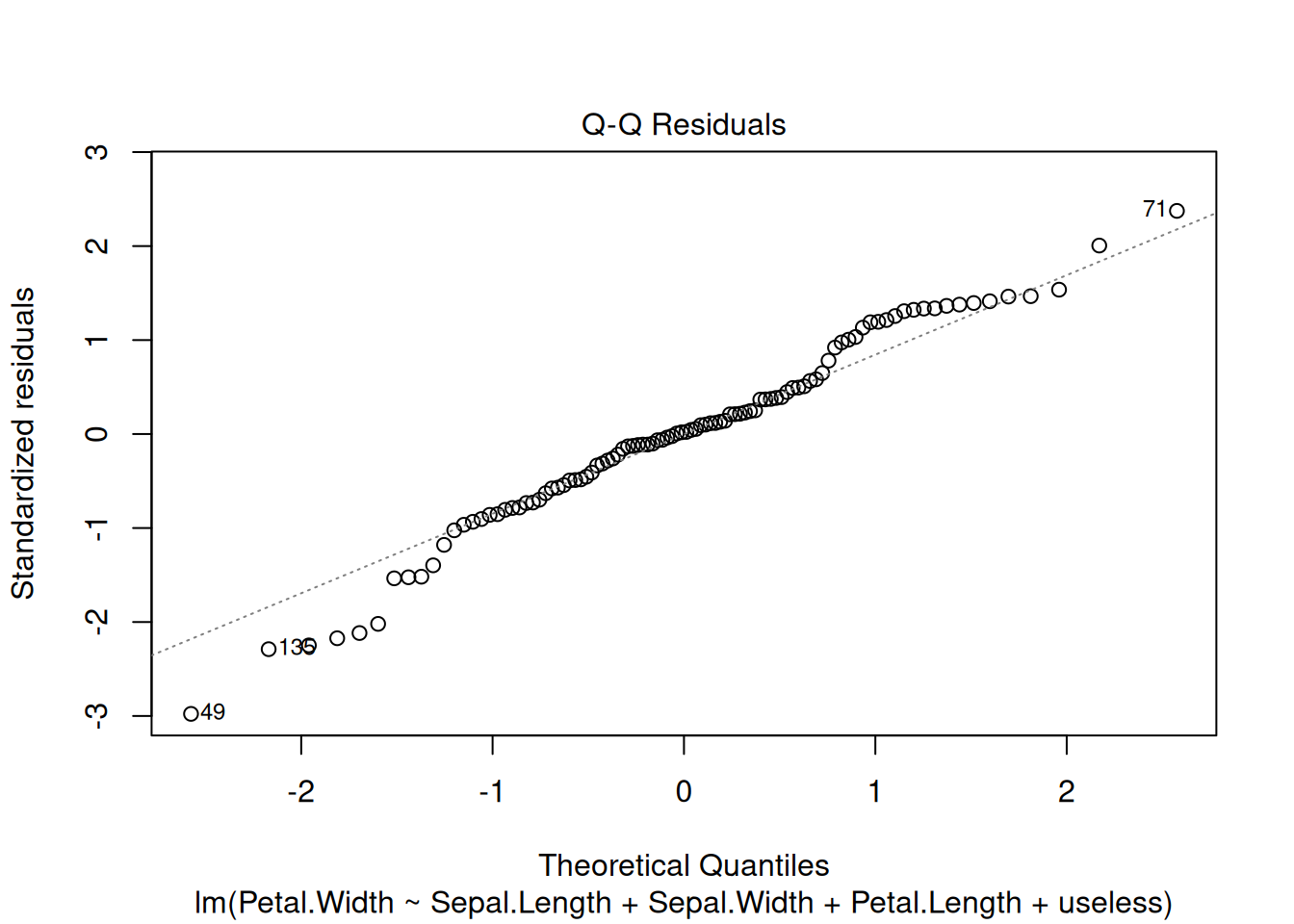
In this case, the two plots look fine.
B.3 Comparing Nested Models
Here we perform model selection to compare several linear models. Nested means that all models use a subset of the same set of features. We create a simpler model by removing the feature useless from the model above.
model2 <- lm(Petal.Width ~ Sepal.Length +
Sepal.Width + Petal.Length,
data = train)
summary(model2)
##
## Call:
## lm(formula = Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length,
## data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.0440 -0.2024 0.0099 0.1998 0.8513
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.1842 0.2076 -0.89 0.38
## Sepal.Length 0.0199 0.0323 0.62 0.54
## Sepal.Width 0.0339 0.0353 0.96 0.34
## Petal.Length 0.3080 0.0180 17.07 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.365 on 96 degrees of freedom
## Multiple R-squared: 0.778, Adjusted R-squared: 0.771
## F-statistic: 112 on 3 and 96 DF, p-value: <2e-16We can remove the intercept by adding -1 to the formula.
model3 <- lm(Petal.Width ~ Sepal.Length +
Sepal.Width + Petal.Length - 1,
data = train)
summary(model3)
##
## Call:
## lm(formula = Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length -
## 1, data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.0310 -0.1961 -0.0051 0.2264 0.8246
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## Sepal.Length -0.00168 0.02122 -0.08 0.94
## Sepal.Width 0.01859 0.03073 0.61 0.55
## Petal.Length 0.30666 0.01796 17.07 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.364 on 97 degrees of freedom
## Multiple R-squared: 0.938, Adjusted R-squared: 0.936
## F-statistic: 486 on 3 and 97 DF, p-value: <2e-16Here is a very simple model.
model4 <- lm(Petal.Width ~ Petal.Length -1,
data = train)
summary(model4)
##
## Call:
## lm(formula = Petal.Width ~ Petal.Length - 1, data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.9774 -0.1957 0.0078 0.2536 0.8455
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## Petal.Length 0.31586 0.00822 38.4 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.362 on 99 degrees of freedom
## Multiple R-squared: 0.937, Adjusted R-squared: 0.936
## F-statistic: 1.47e+03 on 1 and 99 DF, p-value: <2e-16We need a statistical test to compare all these nested models. The appropriate test is called ANOVA (analysis of variance) which is a generalization of the t-test to check if all the treatments (i.e., models) have the same effect. Important note: This only works for nested models. Models are nested only if one model contains all the predictors of the other model.
anova(model1, model2, model3, model4)
## Analysis of Variance Table
##
## Model 1: Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length + useless
## Model 2: Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length
## Model 3: Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length - 1
## Model 4: Petal.Width ~ Petal.Length - 1
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 95 12.8
## 2 96 12.8 -1 -0.0016 0.01 0.91
## 3 97 12.9 -1 -0.1046 0.78 0.38
## 4 99 13.0 -2 -0.1010 0.38 0.69Models 1 is not significantly better than model 2. Model 2 is not significantly better than model 3. Model 3 is not significantly better than model 4! Use model 4, the simplest model.
See anova.lm() for the manual page for ANOVA for linear models.
B.4 Stepwise Variable Selection
Stepwise variable section performs backward (or forward) model selection for linear models and uses the smallest AIC (Akaike information criterion) to decide what variable to remove and when to stop.
s1 <- step(lm(Petal.Width ~ . -Species, data = train))
## Start: AIC=-195.9
## Petal.Width ~ (Sepal.Length + Sepal.Width + Petal.Length + useless +
## Species) - Species
##
## Df Sum of Sq RSS AIC
## - useless 1 0.0 12.8 -197.9
## - Sepal.Length 1 0.0 12.8 -197.5
## - Sepal.Width 1 0.1 12.9 -196.9
## <none> 12.8 -195.9
## - Petal.Length 1 38.6 51.3 -58.7
##
## Step: AIC=-197.9
## Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length
##
## Df Sum of Sq RSS AIC
## - Sepal.Length 1 0.1 12.8 -199.5
## - Sepal.Width 1 0.1 12.9 -198.9
## <none> 12.8 -197.9
## - Petal.Length 1 38.7 51.5 -60.4
##
## Step: AIC=-199.5
## Petal.Width ~ Sepal.Width + Petal.Length
##
## Df Sum of Sq RSS AIC
## - Sepal.Width 1 0.1 12.9 -200.4
## <none> 12.8 -199.5
## - Petal.Length 1 44.7 57.5 -51.3
##
## Step: AIC=-200.4
## Petal.Width ~ Petal.Length
##
## Df Sum of Sq RSS AIC
## <none> 12.9 -200.4
## - Petal.Length 1 44.6 57.6 -53.2
summary(s1)
##
## Call:
## lm(formula = Petal.Width ~ Petal.Length, data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.9848 -0.1873 0.0048 0.2466 0.8343
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0280 0.0743 0.38 0.71
## Petal.Length 0.3103 0.0169 18.38 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.364 on 98 degrees of freedom
## Multiple R-squared: 0.775, Adjusted R-squared: 0.773
## F-statistic: 338 on 1 and 98 DF, p-value: <2e-16Each table represents one step and shows the AIC when each variable is removed and
the one with the smallest AIC (in the first table useless) is removed. It stops
with a small model that only uses Petal.Length.
B.5 Modeling with Interaction Terms
Linear regression models the effect of each predictor separately
using a \(\beta\) coefficient.
What if two variables are only important together?
This is called an interaction between predictors and is modeled using
interaction terms.
In R’s formula() we can use : and *
to specify interactions. For linear regression, an interaction
means that a new predictor is created by multiplying the two original
predictors.
We can create a model with an interaction terms between Sepal.Length, Sepal.Width and
Petal.Length.
model5 <- step(lm(Petal.Width ~ Sepal.Length *
Sepal.Width * Petal.Length,
data = train))
## Start: AIC=-196.4
## Petal.Width ~ Sepal.Length * Sepal.Width * Petal.Length
##
## Df Sum of Sq RSS
## <none> 11.9
## - Sepal.Length:Sepal.Width:Petal.Length 1 0.265 12.2
## AIC
## <none> -196
## - Sepal.Length:Sepal.Width:Petal.Length -196
summary(model5)
##
## Call:
## lm(formula = Petal.Width ~ Sepal.Length * Sepal.Width * Petal.Length,
## data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.1064 -0.1882 0.0238 0.1767 0.8577
##
## Coefficients:
## Estimate Std. Error
## (Intercept) -2.4207 1.3357
## Sepal.Length 0.4484 0.2313
## Sepal.Width 0.5983 0.3845
## Petal.Length 0.7275 0.2863
## Sepal.Length:Sepal.Width -0.1115 0.0670
## Sepal.Length:Petal.Length -0.0833 0.0477
## Sepal.Width:Petal.Length -0.0941 0.0850
## Sepal.Length:Sepal.Width:Petal.Length 0.0201 0.0141
## t value Pr(>|t|)
## (Intercept) -1.81 0.073 .
## Sepal.Length 1.94 0.056 .
## Sepal.Width 1.56 0.123
## Petal.Length 2.54 0.013 *
## Sepal.Length:Sepal.Width -1.66 0.100 .
## Sepal.Length:Petal.Length -1.75 0.084 .
## Sepal.Width:Petal.Length -1.11 0.272
## Sepal.Length:Sepal.Width:Petal.Length 1.43 0.157
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.36 on 92 degrees of freedom
## Multiple R-squared: 0.792, Adjusted R-squared: 0.777
## F-statistic: 50.2 on 7 and 92 DF, p-value: <2e-16
anova(model5, model4)
## Analysis of Variance Table
##
## Model 1: Petal.Width ~ Sepal.Length * Sepal.Width * Petal.Length
## Model 2: Petal.Width ~ Petal.Length - 1
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 92 11.9
## 2 99 13.0 -7 -1.01 1.11 0.36Some interaction terms are significant in the new model, but ANOVA shows that model 5 is not significantly better than model 4
B.6 Prediction
We preform here a prediction for the held out test set.
test[1:5,]
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 128 8.017 1.541 3.515 1.8
## 92 5.268 4.064 6.064 1.4
## 50 5.461 4.161 1.117 0.2
## 134 6.055 2.951 4.599 1.5
## 8 4.900 5.096 1.086 0.2
## useless Species
## 128 6.110 virginica
## 92 4.938 versicolor
## 50 6.373 setosa
## 134 5.595 virginica
## 8 7.270 setosa
test[1:5,]$Petal.Width
## [1] 1.8 1.4 0.2 1.5 0.2
predict(model4, test[1:5,])
## 128 92 50 134 8
## 1.1104 1.9155 0.3529 1.4526 0.3429The most used error measure for regression is the RMSE root-mean-square error.
RMSE <- function(predicted, true) mean((predicted-true)^2)^.5
RMSE(predict(model4, test), test$Petal.Width)
## [1] 0.3874We can also visualize the quality of the prediction using a simple scatter plot of predicted vs. actual values.
plot(test[,"Petal.Width"], predict(model4, test),
xlim=c(0,3), ylim=c(0,3),
xlab = "actual", ylab = "predicted",
main = "Petal.Width")
abline(0,1, col="red")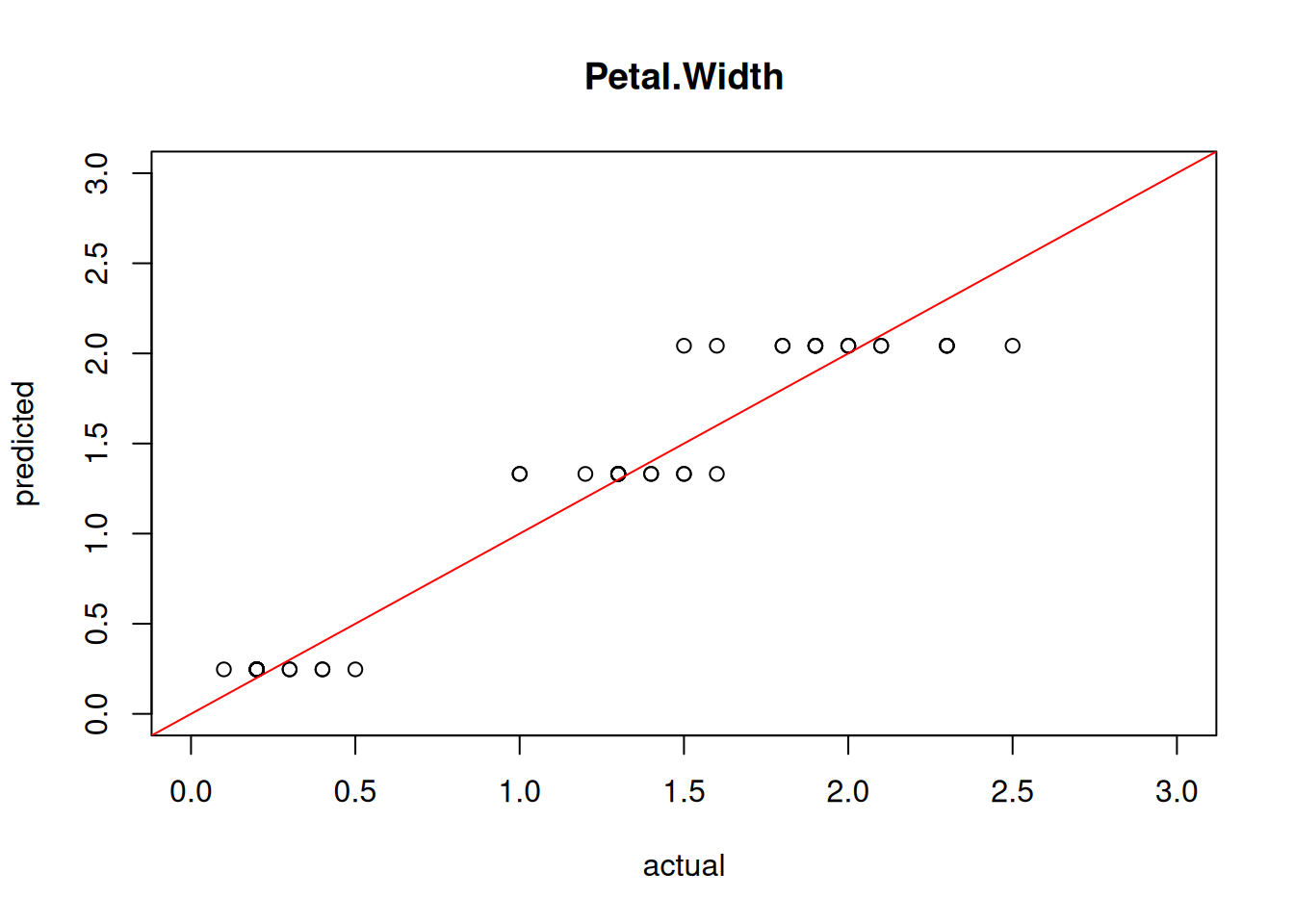
Perfect predictions would be on the red line, the farther they are away, the larger the error.
B.7 Using Nominal Variables
Dummy variables also called one-hot encoding in machine learning is used for factors (i.e., levels are translated into individual 0-1 variable). The first level of factors is automatically used as the reference and the other levels are presented as 0-1 dummy variables called contrasts.
levels(train$Species)
## [1] "setosa" "versicolor" "virginica"model.matrix() is used internally to create dummy variables when the design matrix
for the regression is created..
head(model.matrix(Petal.Width ~ ., data=train))
## (Intercept) Sepal.Length Sepal.Width Petal.Length
## 85 1 2.980 1.464 5.227
## 104 1 5.096 3.044 5.187
## 30 1 4.361 2.832 1.861
## 53 1 8.125 2.406 5.526
## 143 1 6.372 1.565 6.147
## 142 1 6.526 3.697 5.708
## useless Speciesversicolor Speciesvirginica
## 85 5.712 1 0
## 104 6.569 0 1
## 30 4.299 0 0
## 53 6.124 1 0
## 143 6.553 0 1
## 142 5.222 0 1Note that there is no dummy variable for species Setosa, because it is
used as the reference (when the other two dummy variables are 0).
It is often useful to set the reference level.
A simple way is to use the
function relevel() to change which factor is listed first.
Let us perform model selection using AIC on the training data and then evaluate the final model on the held out test set to estimate the generalization error.
model6 <- step(lm(Petal.Width ~ ., data=train))
## Start: AIC=-308.4
## Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length + useless +
## Species
##
## Df Sum of Sq RSS AIC
## - Sepal.Length 1 0.01 3.99 -310
## - Sepal.Width 1 0.01 3.99 -310
## - useless 1 0.02 4.00 -310
## <none> 3.98 -308
## - Petal.Length 1 0.47 4.45 -299
## - Species 2 8.78 12.76 -196
##
## Step: AIC=-310.2
## Petal.Width ~ Sepal.Width + Petal.Length + useless + Species
##
## Df Sum of Sq RSS AIC
## - Sepal.Width 1 0.01 4.00 -312
## - useless 1 0.02 4.00 -312
## <none> 3.99 -310
## - Petal.Length 1 0.49 4.48 -300
## - Species 2 8.82 12.81 -198
##
## Step: AIC=-311.9
## Petal.Width ~ Petal.Length + useless + Species
##
## Df Sum of Sq RSS AIC
## - useless 1 0.02 4.02 -313
## <none> 4.00 -312
## - Petal.Length 1 0.48 4.48 -302
## - Species 2 8.95 12.95 -198
##
## Step: AIC=-313.4
## Petal.Width ~ Petal.Length + Species
##
## Df Sum of Sq RSS AIC
## <none> 4.02 -313
## - Petal.Length 1 0.50 4.52 -304
## - Species 2 8.93 12.95 -200
model6
##
## Call:
## lm(formula = Petal.Width ~ Petal.Length + Species, data = train)
##
## Coefficients:
## (Intercept) Petal.Length Speciesversicolor
## 0.1597 0.0664 0.8938
## Speciesvirginica
## 1.4903
summary(model6)
##
## Call:
## lm(formula = Petal.Width ~ Petal.Length + Species, data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.7208 -0.1437 0.0005 0.1254 0.5460
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.1597 0.0441 3.62 0.00047 ***
## Petal.Length 0.0664 0.0192 3.45 0.00084 ***
## Speciesversicolor 0.8938 0.0746 11.98 < 2e-16 ***
## Speciesvirginica 1.4903 0.1020 14.61 < 2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.205 on 96 degrees of freedom
## Multiple R-squared: 0.93, Adjusted R-squared: 0.928
## F-statistic: 427 on 3 and 96 DF, p-value: <2e-16
RMSE(predict(model6, test), test$Petal.Width)
## [1] 0.1885
plot(test[,"Petal.Width"], predict(model6, test),
xlim=c(0,3), ylim=c(0,3),
xlab = "actual", ylab = "predicted",
main = "Petal.Width")
abline(0,1, col="red")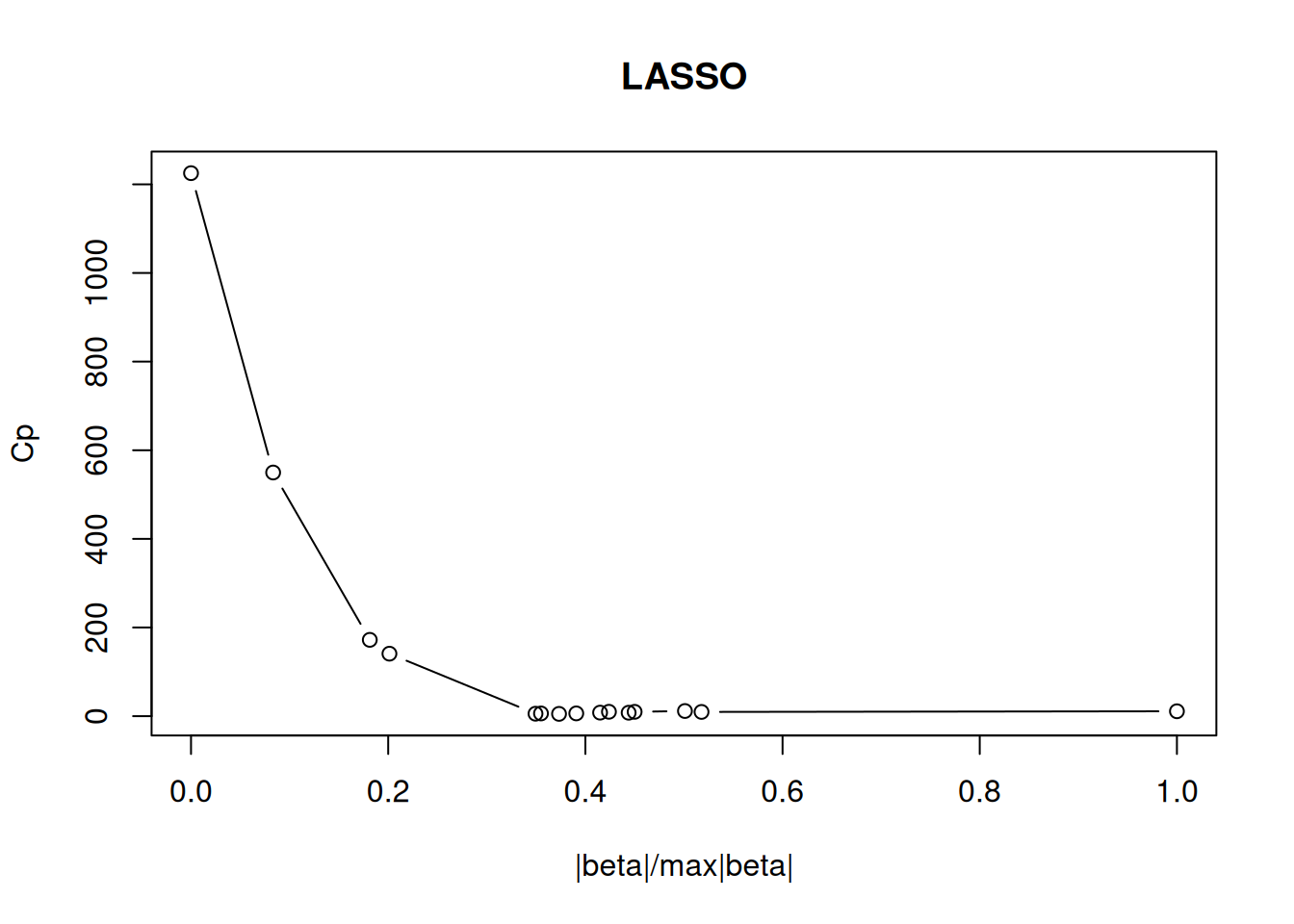
We see that the Species variable provides information to improve the regression model.
B.8 Alternative Regression Models
B.8.1 Regression Trees
Many models used for classification can also perform regression.
For example CART implemented in rpart performs regression
by estimating a value for each leaf note.
Regression is always performed by rpart() when the response variable
is not a factor().
library(rpart)
library(rpart.plot)
model7 <- rpart(Petal.Width ~ ., data = train,
control = rpart.control(cp = 0.01))
model7
## n= 100
##
## node), split, n, deviance, yval
## * denotes terminal node
##
## 1) root 100 57.5700 1.2190
## 2) Species=setosa 32 0.3797 0.2469 *
## 3) Species=versicolor,virginica 68 12.7200 1.6760
## 6) Species=versicolor 35 1.5350 1.3310 *
## 7) Species=virginica 33 2.6010 2.0420 *
rpart.plot(model7) The regression tree shows the predicted value in as the top number in the node.
Also, remember that tree-based models automatically variable selection
by choosing the splits.
The regression tree shows the predicted value in as the top number in the node.
Also, remember that tree-based models automatically variable selection
by choosing the splits.Let’s evaluate the regression tree by calculating the RMSE.
And visualize the quality.
plot(test[,"Petal.Width"], pred,
xlim = c(0,3), ylim = c(0,3),
xlab = "actual", ylab = "predicted",
main = "Petal.Width")
abline(0,1, col = "red")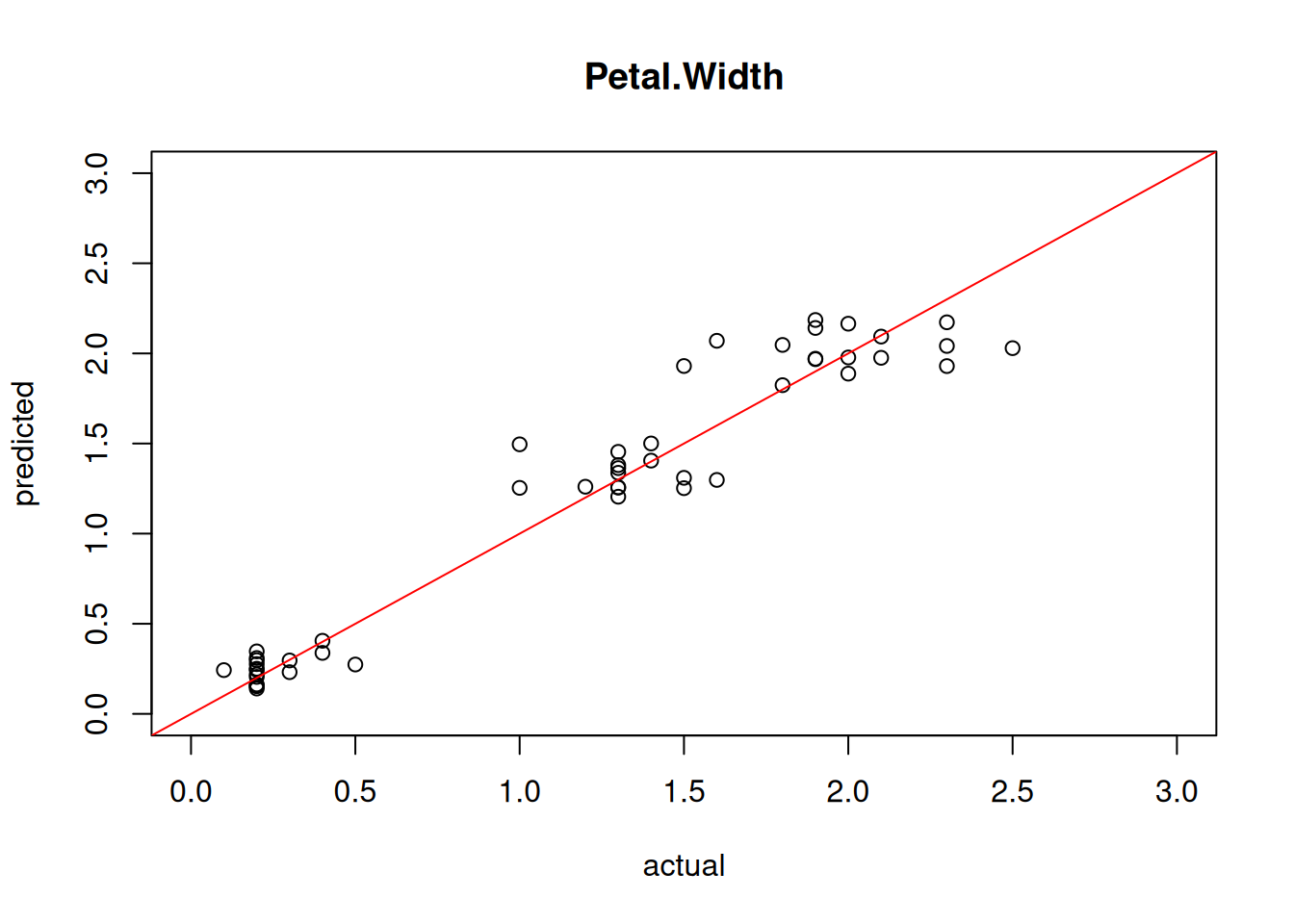
cor(test[,"Petal.Width"], pred)
## [1] 0.9717The plot and the correlation coefficient indicate that the model is very good. In the plot we see an important property of this method which is that it predicts exactly the same value when the data falls in the same leaf node.
B.8.2 Regularized Regression
LASSO (least absolute shrinkage and selection operator)
uses L1 regularization to reduce to perform automatic variable selection.
The regularization adds a penalty for the L1 norm of the parameter vector \(\boldsymbol{\beta}\) (i.e., the summ of all
parameter values)
to the optimization. Increasing the weight of this penalty term (the weight is called \(\lambda\))
results in more and more weights being pushed to 0 which effectively reduces the number of
parameters used in the regression.
An implementation called
the elastic net
is available as the function lars() in package lars.
We create a design matrix (with dummy variables and interaction terms).
lm() did this automatically for us, but for this lars() implementation
we have to do it manually.
x <- model.matrix(~ . + Sepal.Length*Sepal.Width*Petal.Length ,
data = train[, -4])
head(x)
## (Intercept) Sepal.Length Sepal.Width Petal.Length
## 85 1 2.980 1.464 5.227
## 104 1 5.096 3.044 5.187
## 30 1 4.361 2.832 1.861
## 53 1 8.125 2.406 5.526
## 143 1 6.372 1.565 6.147
## 142 1 6.526 3.697 5.708
## useless Speciesversicolor Speciesvirginica
## 85 5.712 1 0
## 104 6.569 0 1
## 30 4.299 0 0
## 53 6.124 1 0
## 143 6.553 0 1
## 142 5.222 0 1
## Sepal.Length:Sepal.Width Sepal.Length:Petal.Length
## 85 4.362 15.578
## 104 15.511 26.431
## 30 12.349 8.114
## 53 19.546 44.900
## 143 9.972 39.168
## 142 24.126 37.253
## Sepal.Width:Petal.Length
## 85 7.650
## 104 15.787
## 30 5.269
## 53 13.294
## 143 9.620
## 142 21.103
## Sepal.Length:Sepal.Width:Petal.Length
## 85 22.80
## 104 80.45
## 30 22.98
## 53 108.01
## 143 61.30
## 142 137.72
y <- train[, 4]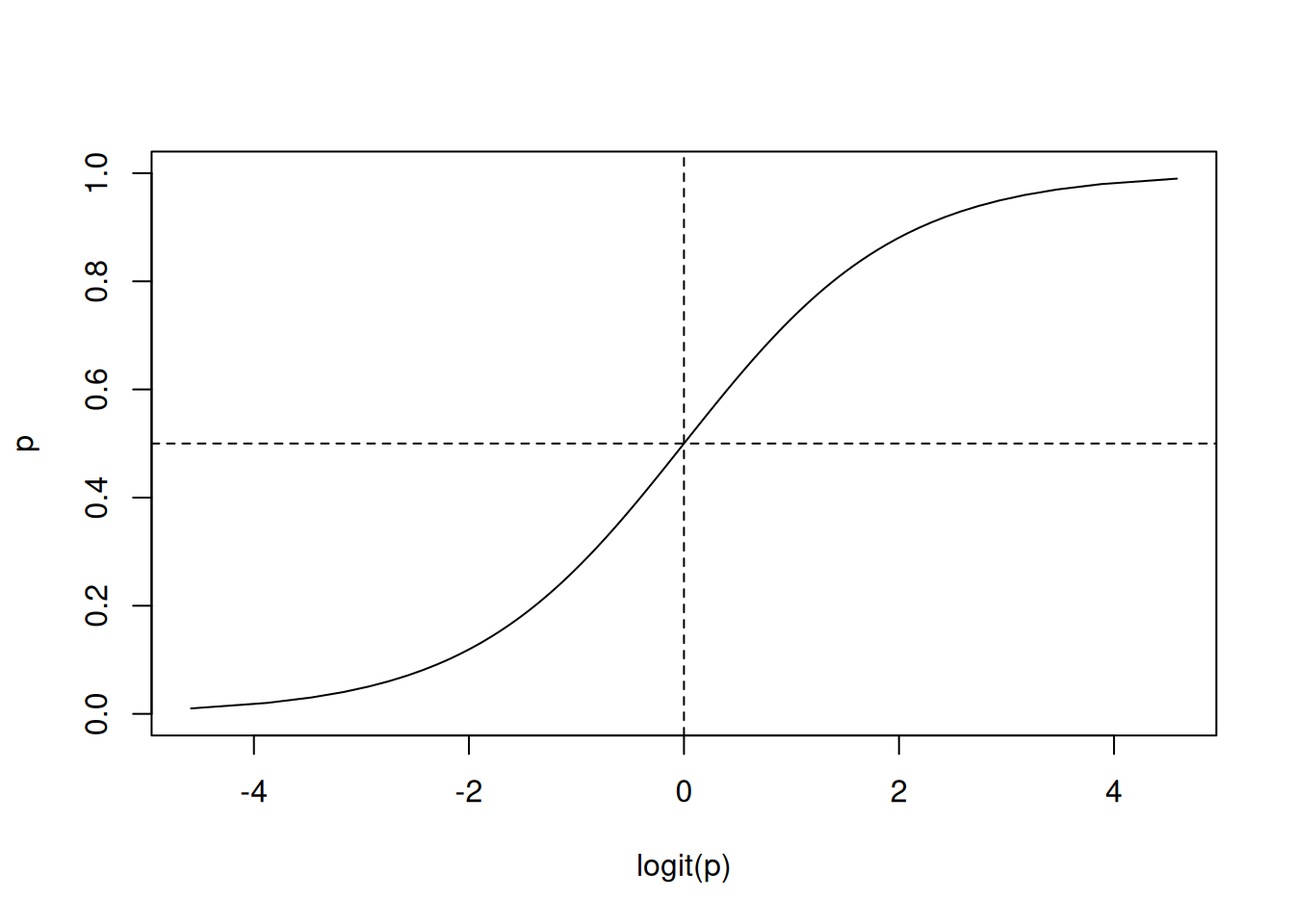
model_lars
##
## Call:
## lars(x = x, y = y)
## R-squared: 0.933
## Sequence of LASSO moves:
## Petal.Length Speciesvirginica Speciesversicolor
## Var 4 7 6
## Step 1 2 3
## Sepal.Width:Petal.Length
## Var 10
## Step 4
## Sepal.Length:Sepal.Width:Petal.Length useless
## Var 11 5
## Step 5 6
## Sepal.Width Sepal.Length:Petal.Length Sepal.Length
## Var 3 9 2
## Step 7 8 9
## Sepal.Width:Petal.Length Sepal.Width:Petal.Length
## Var -10 10
## Step 10 11
## Sepal.Length:Sepal.Width Sepal.Width Sepal.Width
## Var 8 -3 3
## Step 12 13 14The fitted model’s plot shows how variables are added (from left to right to the model).
The text output shoes that Petal.Length is the most important variable added to the model in step 1.
Then Speciesvirginica is added and so on.
This creates a sequence of nested models where one variable is added at a time.
To select the best model Mallows’s Cp statistic
can be used.
plot(model_lars, plottype = "Cp")
best <- which.min(model_lars$Cp)
coef(model_lars, s = best)
## (Intercept)
## 0.0000000
## Sepal.Length
## 0.0000000
## Sepal.Width
## 0.0000000
## Petal.Length
## 0.0603837
## useless
## -0.0086551
## Speciesversicolor
## 0.8463786
## Speciesvirginica
## 1.4181850
## Sepal.Length:Sepal.Width
## 0.0000000
## Sepal.Length:Petal.Length
## 0.0000000
## Sepal.Width:Petal.Length
## 0.0029688
## Sepal.Length:Sepal.Width:Petal.Length
## 0.0003151The variables that are not selected have a \(\beta\) coefficient of 0.
To make predictions with this model, we first have to convert the test data into a design matrix with the dummy variables and interaction terms.
x_test <- model.matrix(~ . + Sepal.Length*Sepal.Width*Petal.Length,
data = test[, -4])
head(x_test)
## (Intercept) Sepal.Length Sepal.Width Petal.Length
## 128 1 8.017 1.541 3.515
## 92 1 5.268 4.064 6.064
## 50 1 5.461 4.161 1.117
## 134 1 6.055 2.951 4.599
## 8 1 4.900 5.096 1.086
## 58 1 5.413 4.728 5.990
## useless Speciesversicolor Speciesvirginica
## 128 6.110 0 1
## 92 4.938 1 0
## 50 6.373 0 0
## 134 5.595 0 1
## 8 7.270 0 0
## 58 7.092 1 0
## Sepal.Length:Sepal.Width Sepal.Length:Petal.Length
## 128 12.35 28.182
## 92 21.41 31.944
## 50 22.72 6.102
## 134 17.87 27.847
## 8 24.97 5.319
## 58 25.59 32.424
## Sepal.Width:Petal.Length
## 128 5.417
## 92 24.647
## 50 4.649
## 134 13.572
## 8 5.531
## 58 28.323
## Sepal.Length:Sepal.Width:Petal.Length
## 128 43.43
## 92 129.83
## 50 25.39
## 134 82.19
## 8 27.10
## 58 153.31Now we can compute the predictions.
predict(model_lars, x_test[1:5,], s = best)
## $s
## 6
## 7
##
## $fraction
## 6
## 0.4286
##
## $mode
## [1] "step"
##
## $fit
## 128 92 50 134 8
## 1.8237 1.5003 0.2505 1.9300 0.2439The prediction is the fit element. We can calculate the RMSE.
And visualize the prediction.
plot(test[,"Petal.Width"],
pred,
xlim=c(0,3), ylim=c(0,3),
xlab = "actual", ylab = "predicted",
main = "Petal.Width")
abline(0,1, col = "red")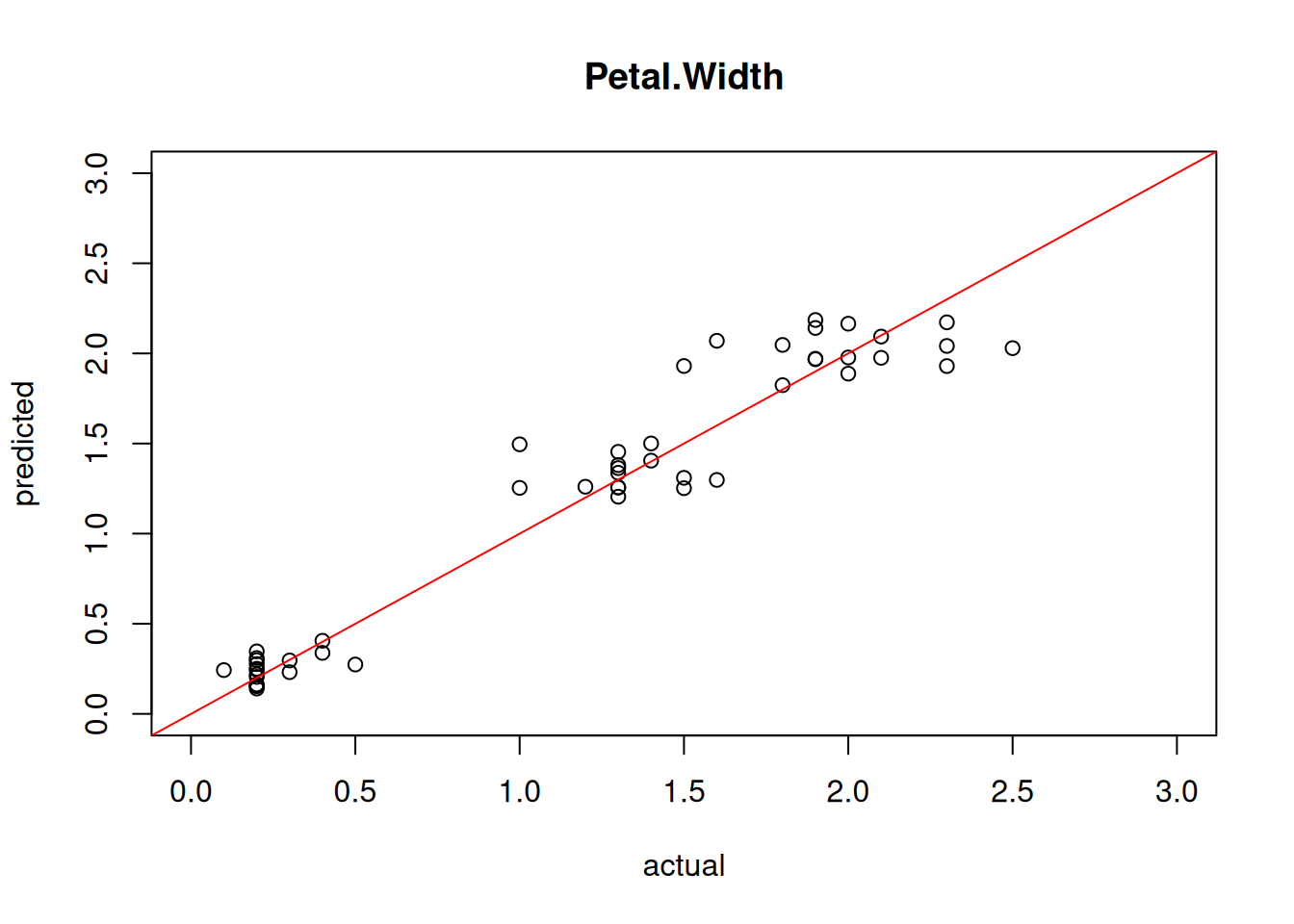
cor(test[,"Petal.Width"],
pred)
## [1] 0.9686The model shows good predictive power on the test set.
B.8.3 ANNs
Regression can be performed using artificial neural networks
with typically a linear final layer.
We will create a network using a single hidden layer
with 3 neurons (a manually tuned hyper parameter) and a linear output layer (set via linout).
library(nnet)
model_nnet <- nnet(Petal.Width ~ ., data = train, size = 3, linout = TRUE)
## # weights: 25
## initial value 82.633473
## iter 10 value 14.094963
## iter 20 value 3.767394
## iter 30 value 3.372093
## iter 40 value 3.264074
## iter 50 value 3.224384
## iter 60 value 3.201191
## iter 70 value 3.182708
## iter 80 value 3.117583
## iter 90 value 3.087831
## iter 100 value 3.009898
## final value 3.009898
## stopped after 100 iterations
model_nnet
## a 6-3-1 network with 25 weights
## inputs: Sepal.Length Sepal.Width Petal.Length useless Speciesversicolor Speciesvirginica
## output(s): Petal.Width
## options were - linear output unitsAnd visualize the quality.
plot(test[,"Petal.Width"], pred,
xlim = c(0,3), ylim = c(0,3),
xlab = "actual", ylab = "predicted",
main = "Petal.Width")
abline(0,1, col = "red")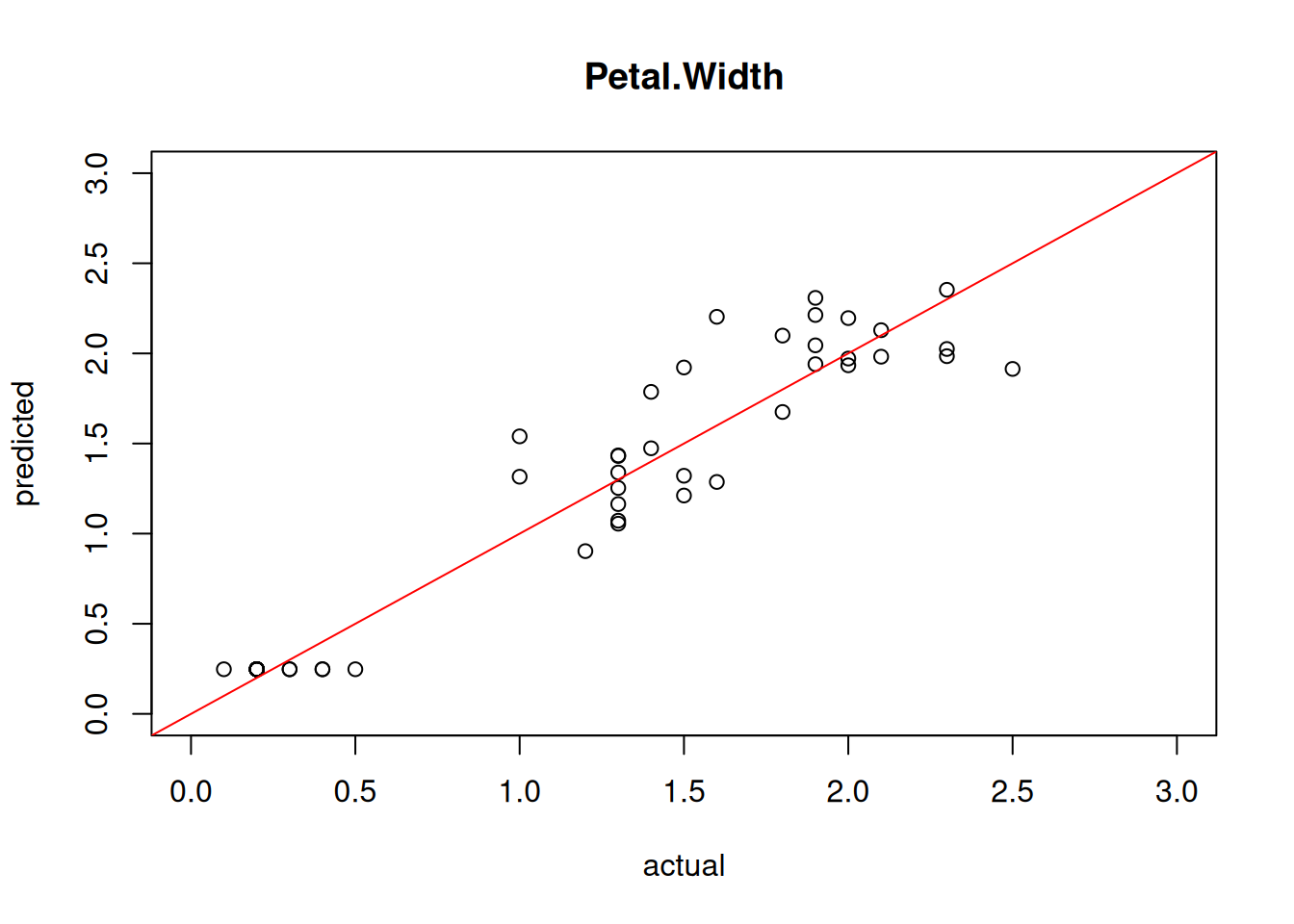
cor(test[,"Petal.Width"], pred)
## [,1]
## [1,] 0.9546Note: It is often necessary to scale the inputs to the ANN so it can learn effectively. It is very popular to scale all inputs to the ranges \([0,1]\) or \([-1,1]\). The ranges of the Iris dataset are fine, so there was no need for scaling.
B.9 Exercises
We will again use the Palmer penguin data for the exercises.
library(palmerpenguins)
head(penguins)
## # A tibble: 6 × 8
## species island bill_length_mm bill_depth_mm
## <chr> <chr> <dbl> <dbl>
## 1 Adelie Torgersen 39.1 18.7
## 2 Adelie Torgersen 39.5 17.4
## 3 Adelie Torgersen 40.3 18
## 4 Adelie Torgersen NA NA
## 5 Adelie Torgersen 36.7 19.3
## 6 Adelie Torgersen 39.3 20.6
## # ℹ 4 more variables: flipper_length_mm <dbl>,
## # body_mass_g <dbl>, sex <chr>, year <dbl>Create an R markdown document that performs the following:
Create a linear regression model to predict the weight of a penguin (
body_mass_g).How high is the R-squared. What does it mean.
What variables are significant, what are not?
Use stepwise variable selection to remove unnecessary variables.
-
Predict the weight for the following new penguin:
new_penguin <- tibble( species = factor("Adelie", levels = c("Adelie", "Chinstrap", "Gentoo")), island = factor("Dream", levels = c("Biscoe", "Dream", "Torgersen")), bill_length_mm = 39.8, bill_depth_mm = 19.1, flipper_length_mm = 184, body_mass_g = NA, sex = factor("male", levels = c("female", "male")), year = 2007 ) new_penguin ## # A tibble: 1 × 8 ## species island bill_length_mm bill_depth_mm ## <fct> <fct> <dbl> <dbl> ## 1 Adelie Dream 39.8 19.1 ## # ℹ 4 more variables: flipper_length_mm <dbl>, ## # body_mass_g <lgl>, sex <fct>, year <dbl> Create a regression tree. Look at the tree and explain what it does. Then use the regression tree to predict the weight for the above penguin.