C Logistic Regression
This chapter introduces the popular classification method logistic regression more in detail. Logistic regression is introduced as an alternative classification method in Chapter 4 of Introduction to Data Mining.
pkgs <- c("glmnet", "caret")
pkgs_install <- pkgs[!(pkgs %in% installed.packages()[,"Package"])]
if(length(pkgs_install)) install.packages(pkgs_install)The packages used for this chapter are:
- caret (Kuhn 2024)
- glmnet (Friedman et al. 2023)
C.1 Introduction
Logistic regression contains the word regression, but it is actually a statistical classification model to predict the probability \(p\) of a binary outcome given a set of features. It is a very powerful classification model that can be fit very quickly. It is one of the first classification models you should try on new data.
Logistic regression is a generalized linear model with the logit as the link function and a binomial error distribution. It can be thought of as a linear regression with the log odds ratio (logit) of the binary outcome as the dependent variable:
\[logit(p) = ln\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...\]
The logit function links the probability p to the linear regression by converting a number in the probability range \([0,1]\) to the range \([-\infty,+\infty]\).
logit <- function(p) log(p/(1-p))
p <- seq(0, 1, length.out = 100)
plot(logit(p), p, type = "l")
abline(h = 0.5, lty = 2)
abline(v = 0, lty = 2)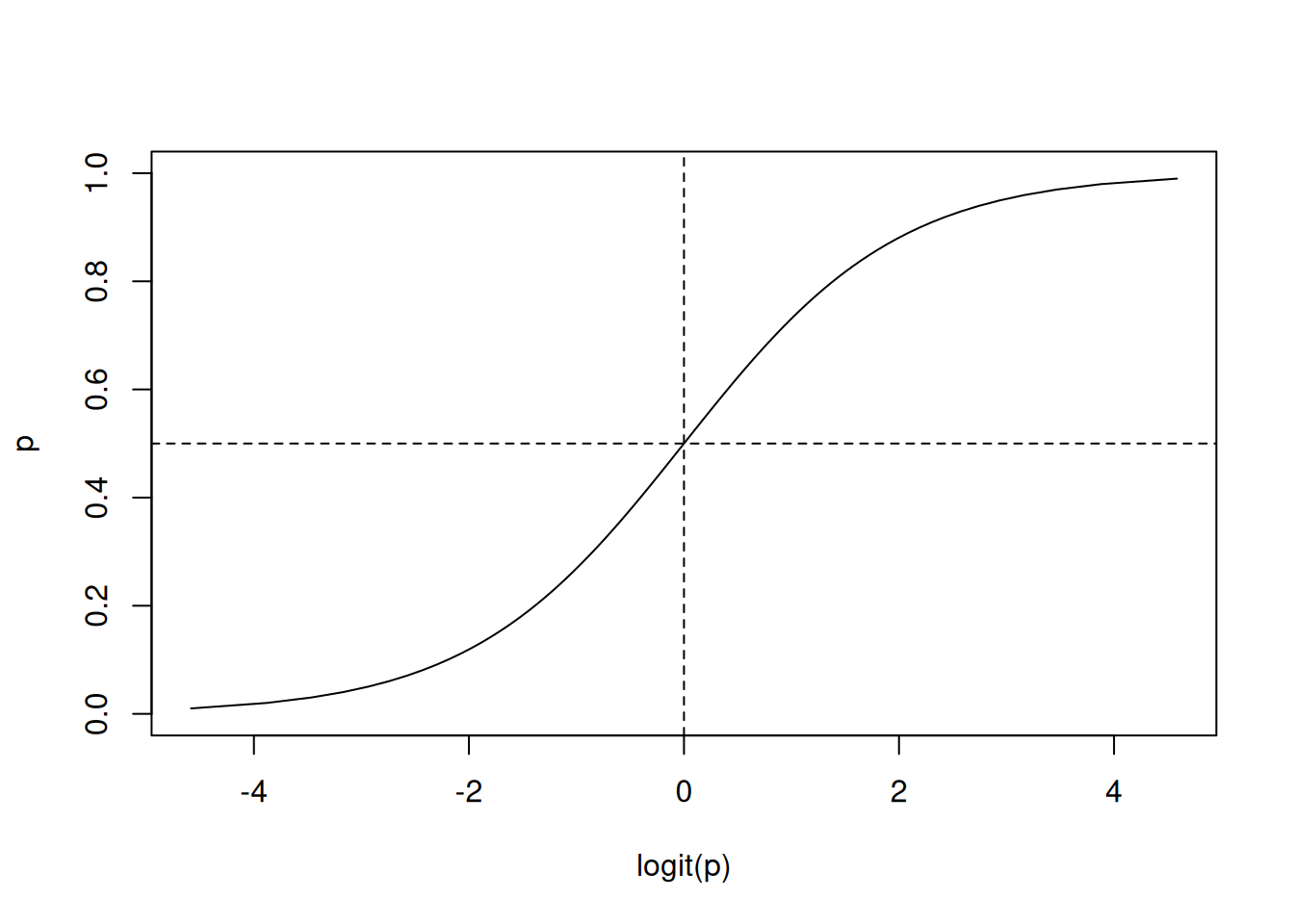
The figure above shows actually the inverse of the logit function. The inverse of the logit function is called logistic (or sigmoid) function (\(\sigma(\cdot)\)) which is often used in ML, and especially for artificial neural networks, to squash the set of real numbers to the \([0,1]\) interval. Using the inverse function, we see that the probability of the outcome \(p\) is modeled by the logistic function of the linear regression:
\[ p = \frac{e^{\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...}}{1 + e^{\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...}} = \frac{1}{1+e^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...)}} = \sigma(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ...)\]
After the \(\boldsymbol{\beta} = (\beta_0, \beta_1,...)\) parameter vector is fitted using training data by minimizing the log loss (i.e., cross-entropy loss), the equation above can be used to predict the probability \(p\) given a new data point \(\mathbf{x} = (x_1, x_2, ...)\). If the predicted \(p > .5\) then we predict that the event happens, otherwise we predict that it does not happen.
The outcome itself is binary and therefore has a Bernoulli distribution. Since we have multiple examples in our data we draw several times from this distribution resulting in a Binomial distribution for the number of successful events drawn. Logistic regression therefore uses a logit link function to link the probability of the event to the linear regression and the distribution family is Binomial.
C.2 Data Preparation
We load and shuffle the data. We also add a useless variable to see if the logistic regression removes it.
data(iris)
set.seed(100) # for reproducability
x <- iris[sample(1:nrow(iris)),]
x <- cbind(x, useless = rnorm(nrow(x)))We create a binary classification problem by
asking if a flower is of species Virginica or not.
We create new logical variable called virginica and remove the
Species column.
x$virginica <- x$Species == "virginica"
x$Species <- NULLWe can visualize the data using a scatter plot matrix and use the color red for
virginica == TRUE and black for the other flowers.
plot(x, col=x$virginica + 1)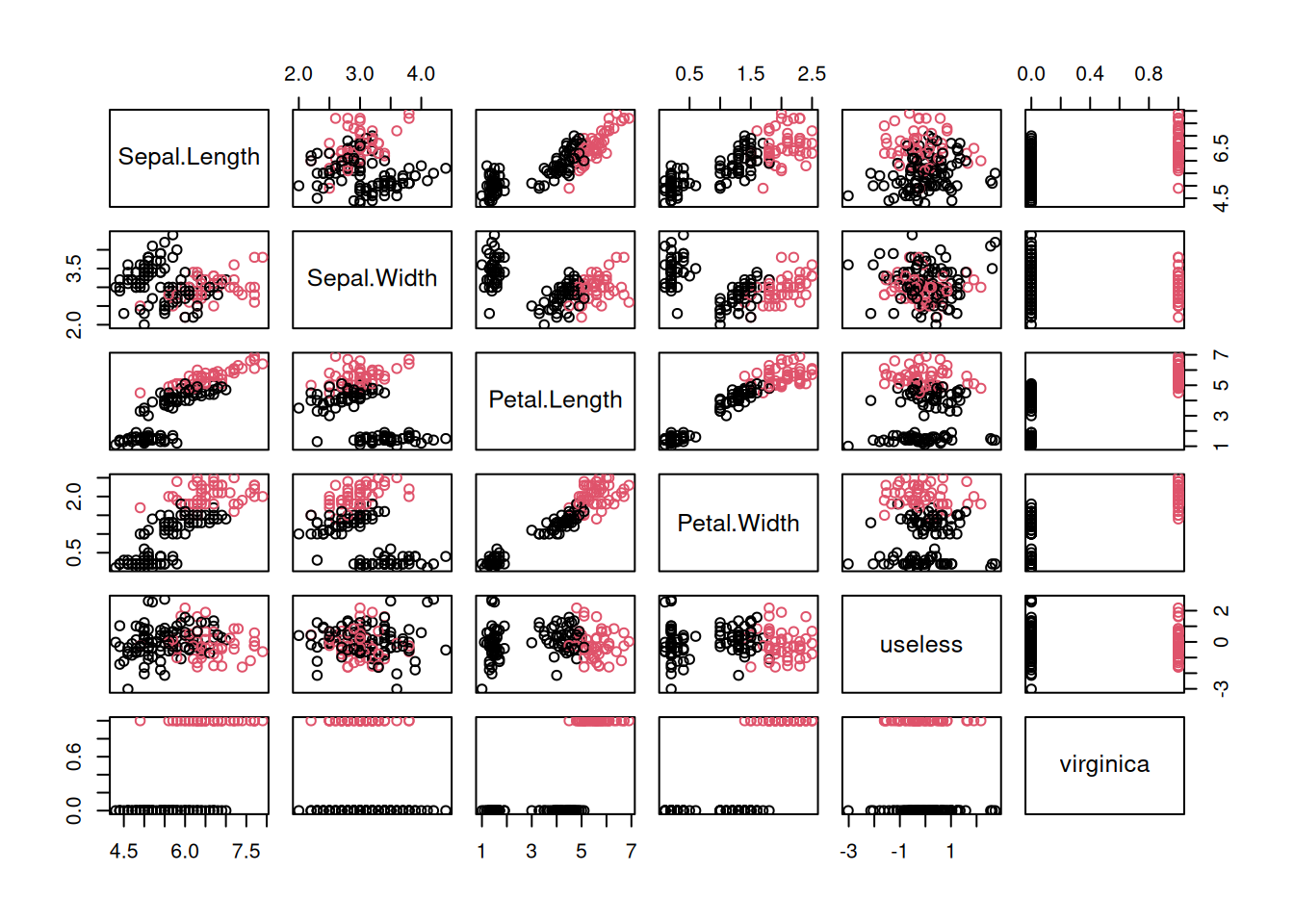
C.3 A first Logistic Regression Model
Logistic regression is a generalized linear model (GLM) with logit as the
link function and a binomial distribution. The glm() function is provided by
the R core package stats which is installed with R and automatically loads
when R is started.
model <- glm(virginica ~ .,
family = binomial(logit), data = x)
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurredAbout the warning: glm.fit: fitted probabilities numerically 0 or 1 occurred means that the data is possibly linearly separable.
model
##
## Call: glm(formula = virginica ~ ., family = binomial(logit), data = x)
##
## Coefficients:
## (Intercept) Sepal.Length Sepal.Width Petal.Length
## -41.649 -2.531 -6.448 9.376
## Petal.Width useless
## 17.696 0.098
##
## Degrees of Freedom: 149 Total (i.e. Null); 144 Residual
## Null Deviance: 191
## Residual Deviance: 11.9 AIC: 23.9Check which features are significant?
summary(model)
##
## Call:
## glm(formula = virginica ~ ., family = binomial(logit), data = x)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -41.649 26.556 -1.57 0.117
## Sepal.Length -2.531 2.458 -1.03 0.303
## Sepal.Width -6.448 4.794 -1.34 0.179
## Petal.Length 9.376 4.763 1.97 0.049 *
## Petal.Width 17.696 10.632 1.66 0.096 .
## useless 0.098 0.807 0.12 0.903
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 190.954 on 149 degrees of freedom
## Residual deviance: 11.884 on 144 degrees of freedom
## AIC: 23.88
##
## Number of Fisher Scoring iterations: 12AIC (Akaike information criterion) is a measure of how good the model is. Smaller is better. It can be used for model selection.
The parameter estimates in the coefficients table are log odds. The * and .
indicate if the effect of the parameter is significantly different from 0.
Positive numbers
mean that increasing the variable increases the predicted probability
and negative numbers mean that the probability decreases. For example,
observing a larger Petal.Length increases the predicted probability for the flower to
be of class Virginica. This effect is significant and you can
verify it in the scatter plot above. For Petal.Length, the red dots have
larger values than
the black dots.
C.4 Stepwise Variable Selection
Only two variables were flagged as significant. We can remove insignificant
variables by trying to remove one variable at a time
as long as the model does not significantly deteriorate (according to the AIC).
This variable selection process is done automatically by the step() function.
model2 <- step(model, data = x)
## Start: AIC=23.88
## virginica ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width +
## useless
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Df Deviance AIC
## - useless 1 11.9 21.9
## - Sepal.Length 1 13.2 23.2
## <none> 11.9 23.9
## - Sepal.Width 1 14.8 24.8
## - Petal.Width 1 22.4 32.4
## - Petal.Length 1 25.9 35.9
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
##
## Step: AIC=21.9
## virginica ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Df Deviance AIC
## - Sepal.Length 1 13.3 21.3
## <none> 11.9 21.9
## - Sepal.Width 1 15.5 23.5
## - Petal.Width 1 23.8 31.8
## - Petal.Length 1 25.9 33.9
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
##
## Step: AIC=21.27
## virginica ~ Sepal.Width + Petal.Length + Petal.Width
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Warning: glm.fit: fitted probabilities numerically 0 or 1
## occurred
## Df Deviance AIC
## <none> 13.3 21.3
## - Sepal.Width 1 20.6 26.6
## - Petal.Length 1 27.4 33.4
## - Petal.Width 1 31.5 37.5
summary(model2)
##
## Call:
## glm(formula = virginica ~ Sepal.Width + Petal.Length + Petal.Width,
## family = binomial(logit), data = x)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -50.53 23.99 -2.11 0.035 *
## Sepal.Width -8.38 4.76 -1.76 0.079 .
## Petal.Length 7.87 3.84 2.05 0.040 *
## Petal.Width 21.43 10.71 2.00 0.045 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 190.954 on 149 degrees of freedom
## Residual deviance: 13.266 on 146 degrees of freedom
## AIC: 21.27
##
## Number of Fisher Scoring iterations: 12The estimates (\(\beta_0, \beta_1,...\) ) are log-odds and can be converted into odds using \(exp(\beta)\). A negative log-odds ratio means that the odds go down with an increase in the value of the predictor. A predictor with a positive log-odds ratio increases the odds. In this case, the odds of looking at a Virginica iris goes down with Sepal.Width and increases with the other two predictors.
C.5 Calculate the Response
Note: we do here in-sample testing on the data we learned the data from. To get a generalization error estimate you should use a test set or cross-validation!
pr <- predict(model2, x, type = "response")
round(pr[1:10], 2)
## 102 112 4 55 70 98 135 7 43 140
## 1.00 1.00 0.00 0.00 0.00 0.00 0.86 0.00 0.00 1.00The response is the predicted probability of the flower being of species Virginica. The probabilities of the first 10 flowers are shown. Below is a histogram of predicted probabilities. The color is used to show the examples that have the true class Virginica.
hist(pr, breaks = 20, main = "Predicted Probability vs. True Class")
hist(pr[x$virginica == TRUE], col = "red", breaks = 20, add = TRUE)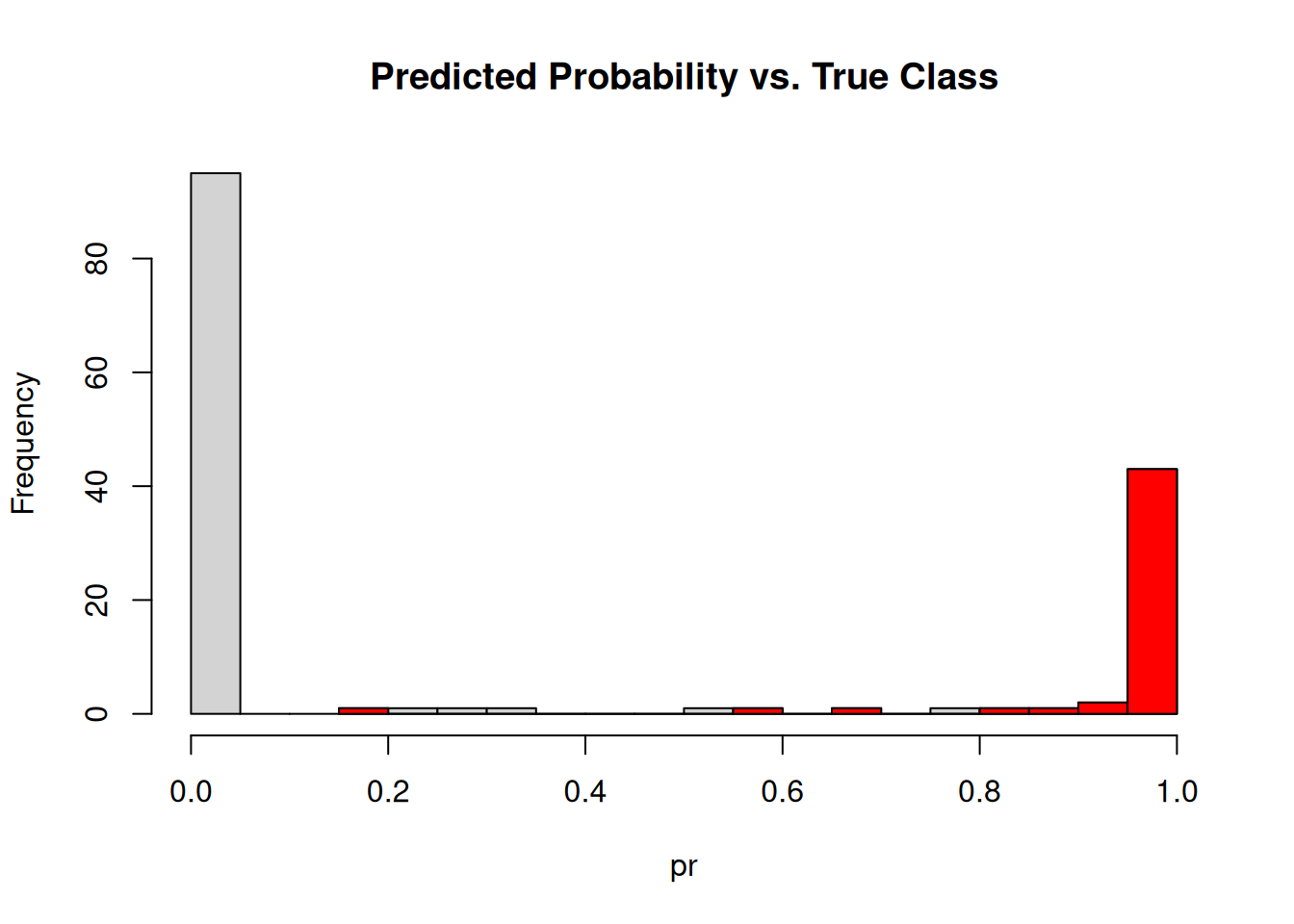
C.6 Check Classification Performance
Here we perform in-sample evaluation on the training set. To get an estimate for generalization error, we should calculate the performance on a held out test set.
The predicted class is calculated by checking if the predicted probability is larger than .5.
pred <- pr > .5Now we can create a confusion table and calculate the accuracy.
tbl <- table(predicted = pred, actual = x$virginica)
tbl
## actual
## predicted FALSE TRUE
## FALSE 98 1
## TRUE 2 49
sum(diag(tbl))/sum(tbl)
## [1] 0.98We can also use caret’s more advanced function caret::confusionMatrix(). Our code
above uses logical vectors. For caret, we need to make sure that both,
the reference and the predictions are coded as factor.
caret::confusionMatrix(
reference = factor(x$virginica, labels = c("Yes", "No"), levels = c(TRUE, FALSE)),
data = factor(pred, labels = c("Yes", "No"), levels = c(TRUE, FALSE)))
## Confusion Matrix and Statistics
##
## Reference
## Prediction Yes No
## Yes 49 2
## No 1 98
##
## Accuracy : 0.98
## 95% CI : (0.943, 0.996)
## No Information Rate : 0.667
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.955
##
## Mcnemar's Test P-Value : 1
##
## Sensitivity : 0.980
## Specificity : 0.980
## Pos Pred Value : 0.961
## Neg Pred Value : 0.990
## Prevalence : 0.333
## Detection Rate : 0.327
## Detection Prevalence : 0.340
## Balanced Accuracy : 0.980
##
## 'Positive' Class : Yes
## We see that the model performs well with a very high accuracy and kappa value.
C.7 Regularized Logistic Regression
glmnet::glmnet() fits generalized linear models (including logistic regression)
using regularization via penalized maximum likelihood.
The regularization parameter \(\lambda\) is a hyperparameter and
glmnet can use cross-validation to find an appropriate
value. glmnet does not have a function interface, so we have
to supply a matrix for X and a vector of responses for y.
library(glmnet)
## Loaded glmnet 4.1-8
X <- as.matrix(x[, 1:5])
y <- x$virginica
fit <- cv.glmnet(X, y, family = "binomial")
fit
##
## Call: cv.glmnet(x = X, y = y, family = "binomial")
##
## Measure: Binomial Deviance
##
## Lambda Index Measure SE Nonzero
## min 0.00164 59 0.126 0.0456 5
## 1se 0.00664 44 0.167 0.0422 3There are several selection rules for lambda, we look at the coefficients of the logistic regression using the lambda that gives the most regularized model such that the cross-validated error is within one standard error of the minimum cross-validated error.
coef(fit, s = fit$lambda.1se)
## 6 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) -16.961
## Sepal.Length .
## Sepal.Width -1.766
## Petal.Length 2.197
## Petal.Width 6.820
## useless .A dot means 0. We see that the predictors Sepal.Length and useless are not used in the prediction giving a models similar to stepwise variable selection above.
A predict function is provided. We need to specify what regularization to use and that we want to predict a class label.
predict(fit, newx = X[1:5,], s = fit$lambda.1se, type = "class")
## s1
## 102 "TRUE"
## 112 "TRUE"
## 4 "FALSE"
## 55 "FALSE"
## 70 "FALSE"Glmnet provides supports many types of generalized linear models. Examples can be found in the article An Introduction to glmnet.
C.8 Multinomial Logistic Regression
Regular logistic regression predicts only one outcome of a binary event represented
by two classes. Extending this model to data with more than two classes
is called multinomial logistic regression,
(or log-linear model).
A popular implementation uses simple artificial neural networks.
Regular logistic regression is equivalent to a single neuron with a
sigmoid (i.e., logistic) activation function optimized with cross-entropy loss.
For multinomial logistic regression, one neuron is used for each class and the
probability distribution is calculated with the softmax activation.
This extension is implemented in nnet::multinom().
set.seed(100)
x <- iris[sample(1:nrow(iris)), ]
model <- nnet::multinom(Species ~., data = x)
## # weights: 18 (10 variable)
## initial value 164.791843
## iter 10 value 16.177348
## iter 20 value 7.111438
## iter 30 value 6.182999
## iter 40 value 5.984028
## iter 50 value 5.961278
## iter 60 value 5.954900
## iter 70 value 5.951851
## iter 80 value 5.950343
## iter 90 value 5.949904
## iter 100 value 5.949867
## final value 5.949867
## stopped after 100 iterations
model
## Call:
## nnet::multinom(formula = Species ~ ., data = x)
##
## Coefficients:
## (Intercept) Sepal.Length Sepal.Width
## versicolor 18.69 -5.458 -8.707
## virginica -23.84 -7.924 -15.371
## Petal.Length Petal.Width
## versicolor 14.24 -3.098
## virginica 23.66 15.135
##
## Residual Deviance: 11.9
## AIC: 31.9We get a \(\boldsymbol{\beta}\) vector with weights for two of the three classes. The third class is used as the default class with all weights set to 0. This can be interpreted as comparing the log odds of each of the two classes with the default class. A positive number means that increasing the variable makes the class more likely and a negative number means the opposite.
Predict the class for the first 5 flowers in the training data.
x[1:5, ]
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 102 5.8 2.7 5.1 1.9
## 112 6.4 2.7 5.3 1.9
## 4 4.6 3.1 1.5 0.2
## 55 6.5 2.8 4.6 1.5
## 70 5.6 2.5 3.9 1.1
## Species
## 102 virginica
## 112 virginica
## 4 setosa
## 55 versicolor
## 70 versicolor
predict(model, x[1:5,])
## [1] virginica virginica setosa versicolor versicolor
## Levels: setosa versicolor virginicaThe package glmnet implements also multinomial logistic regression using
glmnet(..., family = "multinomial").
C.9 Exercises
We will again use the Palmer penguin data for the exercises.
library(palmerpenguins)
head(penguins)
## # A tibble: 6 × 8
## species island bill_length_mm bill_depth_mm
## <chr> <chr> <dbl> <dbl>
## 1 Adelie Torgersen 39.1 18.7
## 2 Adelie Torgersen 39.5 17.4
## 3 Adelie Torgersen 40.3 18
## 4 Adelie Torgersen NA NA
## 5 Adelie Torgersen 36.7 19.3
## 6 Adelie Torgersen 39.3 20.6
## # ℹ 4 more variables: flipper_length_mm <dbl>,
## # body_mass_g <dbl>, sex <chr>, year <dbl>Create an R markdown document that performs the following:
- Create a test and a training data set (see section Holdout Method in Chapter 3).
- Create a logistic regression using the training set to predict the variable sex.
- Use stepwise variable selection. What variables are selected?
- What do the parameters for for each of the selected features tell you?
- Predict the sex of the penguins in the test set. Create a confusion table and calculate the accuracy and discuss how well the model works.